the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
On the reflectance spectroscopy of snow
Alexander Kokhanovsky
Maxim Lamare
Biagio Di Mauro
Ghislain Picard
Laurent Arnaud
Marie Dumont
François Tuzet
Carsten Brockmann
Jason E. Box
We propose a system of analytical equations to retrieve snow grain size and absorption coefficient of pollutants from snow reflectance or snow albedo measurements in the visible and near-infrared regions of the electromagnetic spectrum, where snow single-scattering albedo is close to 1.0. It is assumed that ice grains and impurities (e.g., dust, black and brown carbon) are externally mixed, and that the snow layer is semi-infinite and vertically and horizontally homogeneous. The influence of close-packing effects on reflected light intensity are assumed to be small and ignored. The system of nonlinear equations is solved analytically under the assumption that impurities have the spectral absorption coefficient, which obey the Ångström power law, and the impurities influence the registered spectra only in the visible and not in the near infrared (and vice versa for ice grains). The theory is validated using spectral reflectance measurements and albedo of clean and polluted snow at various locations (Antarctica Dome C, European Alps). A technique to derive the snow albedo (plane and spherical) from reflectance measurements at a fixed observation geometry is proposed. The technique also enables the simulation of hyperspectral snow reflectance measurements in the broad spectral range from ultraviolet to the near infrared for a given snow surface if the actual measurements are performed at a restricted number of wavelengths (two to four, depending on the type of snow and the measurement system).
The reflective properties of clean and polluted snow are of importance for various applications, including climate (Hansen and Nazarenko, 2007) and environmental pollution (Nazarenko et al., 2017) studies. The spectral snow reflectance is usually studied in the framework of the radiative transfer theory. The application of the numerical methods for the solution of the radiative transfer equation for snow layers has been performed by, among others, Mishchenko et al. (1999), Stamnes et al. (2011) and He et al. (2018). The approximate solutions of the radiative transfer equation useful for snow optics and spectroscopy applications have been developed by Warren and Wiscombe (1980), Wiscombe and Warren (1980) and Kokhanovsky and Zege (2004). In this work, we propose an analytical snow albedo and reflectance model which can be used to derive near-surface snow optical and microphysical properties using measurements at just two to four wavelengths in the visible and near infrared depending on the measurement system and type of snow. In particular, we present the method for the determination of snow grain size, absorption Ångström coefficient and spectral absorption coefficient of impurities embedded in the snow matrix assuming an external mixture of snow grains and impurities. The technique to derive the snow albedo from reflectance measurements is also presented. The absorption and extinction of light by snow grains is treated in the framework of a geometrical optical approximation. The absorption coefficient of impurities is modeled using the Ångström power law. All derivations are performed in the framework of the asymptotic radiative transfer theory (see, e.g., Kokhanovsky and Zege, 2004; Zege et al., 2011). It is assumed that the snow layer is vertically and horizontally homogeneous and semi-infinite. Therefore, the effects of the finite layer thickness are ignored.
2.1 The snow reflectance
The snow reflectance R (equal to unity for ideal white Lambertian reflectors; see Appendix A) can be presented in the following way using approximate asymptotic radiative transfer theory (Kokhanovsky and Zege, 2004):
where is the reflectance of a semi-infinite non-absorbing snow layer; ; μ0 is the cosine of the solar zenith angle; μ is the cosine of the viewing zenith angle; and rs is the snow spherical albedo:
where
g is the asymmetry parameter and ω0 is the single-scattering albedo. Let us introduce the probability of photon absorption . It is equal as the ratio of absorption κabs and extinction κext coefficients:
where
The first and second terms in Eq. (5) correspond to the ice grains and pollutants, respectively. We assume that scattering and extinction of light by impurities are much smaller than by ice grains and, therefore (Kokhanovsky and Zege, 2004),
Here, is the effective diameter of ice grains, is the average volume of grains and is their average projected area averaged over all directions (equal to for convex particles in random orientation, where ∑ is the average surface area and c is the volumetric concentration of the snow grains). The value of c is equal to the volume of grains in unit volume of snow (, where N is the number of snow grains in unit volume of snow (cm−3)). It is related to the dry-snow density ρs by the following relation: ρs=cρi, where ρi is the bulk ice density.
The product of the effective diameter d and the bulk ice absorption coefficient α is a small number in the visible and near infrared. Then it follows (Kokhanovsky and Zege, 2004; see their Eq. 37 for the absorption path length inversely proportional to the absorption coefficient) that
where B is the grain-shape-dependent parameter (absorption enhancement parameter) and , where χ is the imaginary part of the ice refractive index at the wavelength λ.
We present the absorption coefficient of pollutants in snow as
where µm and m is the absorption Angstrom coefficient.
It follows from Eqs. (4)–(8) that
where
and therefore
Let the parameter z=y2, from which it follows that
where
and
is the effective absorption length (EAL) and
is a grain-shape-dependent (but not grain-size-dependent) parameter.
The parameter l can be determined directly from reflectance or albedo measurements, enabling also the determination of the grain diameter assuming a particular shape of grains. It has been found that the asymmetry parameter of crystalline clouds is usually in the range 0.74–0.76 in the visible (Garret, 2008). The asymmetry parameter g for snow has not been measured so far in situ, but we shall assume that it is close to that in crystalline clouds and adopt the value 0.75. It follows from experimental studies of Libois et al. (2014) that B=1.6 on average. Therefore, it follows (see Eq. 15) that ξ≈11.38.
Using the EAL, the equations for the snow reflectance and spherical albedo may be simplified.
Namely, it follows that
The plane albedo can be derived as well (Kokhanovsky and Zege, 2004):
The relationship between the albedo and the reflectance R is given in Appendix A. It follows from Eq. (16) that the spectral reflectance of polluted snow is determined by four a priori unknown parameters: l, R0, f and m. They can be estimated from the measurements of reflectance at four wavelengths. This also enables the determination of the spectral reflectance (and albedo; see Eq. 18) at the visible and near-infrared wavelengths at an arbitrary λ. It follows that
where the numbers 1, 2, 3 and 4 signify the wavelengths used. Equations (19)–(22) can be used to compute four unknown parameters given above and, therefore, to determine reflectance and albedo at any wavelength in the visible and the near infrared using Eqs. (16)–(18). Let us assume that the spectral channels are selected in a way that the effects of ice absorption can be neglected in the first two channels (λ1,λ2) and effects of absorption by pollutants are negligible in the second pair of channels (λ3,λ4). This situation is typical of not heavily polluted snow. Then it follows, instead of Eqs. (19)–(22), that
Equations (25) and (26) can be used to find the pair (l,R0):
where and . Then it follows from Eqs. (23) and (24) that
where . In the absence of pollutants, Eq. (27) remains valid. However, the parameters m and f are undefined, and .
One may also derive the impurity absorption coefficient at the wavelength λ0 normalized to the concentration of ice grains c (see Eq. 1):
where f is given by Eq. (29). The normalized absorption coefficient at each wavelength can also be found using Eqs. (8), (28) and (30).
To determine the concentration of pollutants (cp), one must either know in advance or determine the impurity volumetric absorption coefficient, defined as
where is the average absorption cross section of impurities and is the average volume of absorbing impurities. Namely, it follows by definition that
and
where .
The value of K(λ0) can be found if one knows the type of pollutants and their microphysical properties. In particular, it follows for the impurities much smaller than the wavelength λ0 (van de Hulst, 1981) that
where
is the pollutant bulk absorption coefficient, χpol(λ0) is the imaginary part of pollutant refractive index and npol is the real part of the pollutant refractive index,
It follows that F=0.9 for soot (assuming that n=1.75, χpol=0.47 in the visible). One can see that ℂ can be found if one knows the refractive index of absorbing Rayleigh particles in advance.
In particular, it follows for soot impurities that
In the case of non-Rayleigh scatterers, one needs to know not only the refractive index but also the particle size distribution and shape of particles, enabling the determination of the impurity volumetric absorption coefficient K(λ0) and, therefore, the normalized concentration of impurities:
2.2 The snow albedo
2.2.1 Theory
If the plane albedo is the measured physical quantity, one needs to find only three constants: l, f and m.
The respective analytical equations can be presented as
We shall assume that the last channel is not influenced by impurities and the first two channels are not influenced by the absorption of light by grains. Then it follows that
The EAL can be found from Eq. (44):
It follows from Eqs. (42) and (43) that
where ψk=ln2rk.
In the case of unpolluted snow, one derives
Equation (45) can be used to find the effective absorption length and, therefore, the spectral albedo of unpolluted snow at any wavelength using Eq. (47). If not plane but rather spherical albedo is measured, then all equations presented in this section are valid, except one should assume that u=1 and substitute r with rs (Kokhanovsky and Zege, 2004).
3.1 The measurements of the plane albedo
We have applied the technique developed above to the measured spectral plane albedo both for polluted and pure snow. Therefore, in situ spectral albedo measurements were obtained from two different field sites located in the French Alps (polluted snow) and in Antarctica (clean snow).
The spectral albedo of a spring alpine snowpack was measured at the Col du Lautaret field site ( N, E; 2100 m a.s.l.) in the French Alps. The measurements were performed using a non-automated version of the spectrometer system described above. The handheld instrument has a single light collector, located at the end of a 3 m boom placed 1.5 m above the surface. The boom is rotated by the operator to successively acquire the downward and upward solar radiation. The spectral albedo data (each spectral albedo measurement at a given point is an average of five measurements) at several locations close to the Col du Lautaret field site were obtained on 12 April 2017 across a 100 m transect, in an attempt to account for spatial variability. The measurements were acquired in clear-sky conditions, with a solar zenith angle varying between 47.9 and 52.2∘.
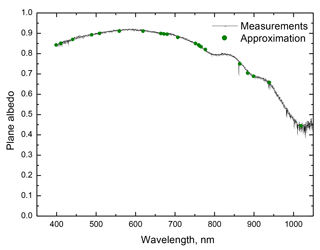
Figure 1The intercomparison of theory (symbols) with experimental measurements of plane albedo (line, no noise removed) performed in the French Alps ( N, E; 2100 m a.s.l.) obtained on 12 April 2017. The plane albedo is an average of five measurements performed between 08:55 and 09:30 UTC for a polluted (by dust) snowpack. The solar zenith angle for the measurements was between 47 and 49∘. The noise of measurements has not been removed and is clearly seen in the near-infrared portion of the spectrum.
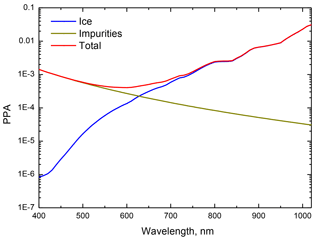
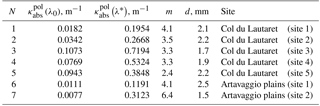
The results of comparison of measurements and the theory presented above are illustrated in Fig. 1 at the Col du Lautaret field site. The parameters l, f and m have been found from Eqs. (42)–(44) and the measurements at the wavelengths λ1=400 nm, λ2=560 nm and λ3=1020 nm. At other measurement sites across a transect the results of the intercomparison are excellent and similar to those presented in Fig. 1. Therefore, the theory can be used to derive snow optical and microphysical properties even for polluted snowpack. The derived spectral probability of photon absorption for the case shown in Fig. 1 is presented in Fig. 2. The derived absorption coefficient (assuming ), the grain diameter d and the absorption Ångström parameter m for five sites across the transect are listed in Table 1 (lines 1–5). It follows that the value of m is in the range 2.4–4.1, consistent with the identified presence of dust particles in snow (Doherty et al., 2010). The pure black carbon impurities have values of m close to 1. The grain diameter is in the range 1.7–2.2 mm, consistent with low values of snow albedo at 1020 nm (see Fig. 1). Wiscombe and Warren (1981) calculated the dependence of the clean-snow spectral albedo at the solar zenith angle 60∘ and several grain radii and presented it in their Fig. 8. It follows from their calculations that the albedo decreases from 0.8 to 0.4 mm, while the diameter of grains changes from 0.1 to 2 mm. It follows from our Fig. 1 that the measured plane albedo is close to 0.45, signifying the dominance of large grains in the snowpack as reported in Table 1.
Table 1The derived snow parameters for the five samples. The value of c is assumed to be equal to 1∕3, which leads to the extinction length () being equal to the effective grain diameter d. The absorption coefficient is given at the wavelengths λ0=1000 nm and nm.
The spectral albedo of pure snow (very low amount of impurities) was measured at Dome C ( S, E) in Antarctica using an automated spectral radiometer (Libois et al., 2015; Picard et al., 2016; Dumont et al., 2017). The instrument is composed of two individual heads located approximately 1.5 m above the surface. Each head contains two cosine receptors facing upward and downward, which receive the incident solar radiation and the reflected radiation. The collectors are connected to an Ocean Optics Maya2000 Pro spectrometer with fiber optics through an optical switch. Radiation is measured over the 350–1100 nm spectral range with an effective spectral resolution of 3 nm. Albedo was calculated as the ratio of the upward and downward spectral irradiance. A full description of the instrument and the processing steps to calculate the spectral albedo are given by Picard et al. (2016). The spectral albedo measurements used here were made on 10 January 2017, with a solar zenith angle of 63.2∘, during clear-sky conditions assessed by ground observations.
The results of the application of the proposed technique to the pure snow (no pollution) albedo measured in Antarctica are illustrated in Fig. 3. Application of our technique results in excellent agreement with measured albedo over pure snow (no pollution) in Antarctica. Because the snow at Dome C is clean/pristine, the value of f is negligible, resulting in snow albedo depending only on the effective absorption length/grain size, which has been derived at a single wavelength (1020 nm). The derived grain diameter for the case presented in Fig. 3 is equal to 0.5 mm. The retrieval error estimation is presented in Appendix B.
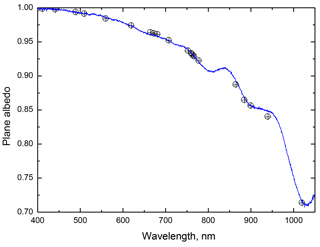
Figure 3The intercomparison of theory (symbols) with experimental measurements of plane albedo (line) performed in Antarctica (Dome C; S, E) for pure snow. The measured plane albedo was obtained on 10 January 2017 at 23:24 UTC, for a solar zenith angle of 63∘. The parameters l, f and m have been derived from the measurements at 400, 560 and 1020 nm.
3.2 The measurements of the spectral reflectance
The application of the developed theory to the measurements of the spectral reflectance is presented in Fig. 4 for two locations with different dust loads (39.6 and 107.4 ppm). The spectral reflectance of snow was measured in the European Alps (Artavaggio plains; 1650 m a.s.l.; N, E) at the solar zenith angle equal to 52∘. The measurements were made on 14 March 2014, after a major transport and deposition of mineral dust from the Sahara. The event was very intense, and it was reported in the recent scientific literature regarding snow optical properties (Di Mauro et al., 2015; Dumont et al., 2017), atmospheric chemistry and physics (Belosi et al., 2017), and microbiology (Weil et al., 2017). The dust transport event deposited fine mineral dust particles from the atmosphere via wet deposition, according to the BSC-DREAM8b model (Basart et al., 2012). Spectral measurements of snow were made using a field spectrometer (Analytical Spectral Devices (ASD) FieldSpec Pro). This instrument features a spectral range of 350–2500 nm, a full width at half maximum of 5–10 nm and a spectral resolution of 1 nm. Data presented here were collected under clear-sky conditions at noon. Incident radiation was estimated using a Lambertian Spectralon panel. Reflected radiance was divided by incident radiance, and the hemispherical conical reflectance factor was calculated for two plots containing 39.6 and 107.4 ppm of dust. Dust concentration was measured with a Coulter counter by integrating particles with a diameter smaller than 18 µm. Spectral measurements were performed at nadir using a bare optical fiber (field of view of 25∘) at 80 cm from the snow sample. Both the optical fiber and the spectralon panel were equipped with an optical level. Further details on this dataset can be found in Di Mauro et al. (2015).
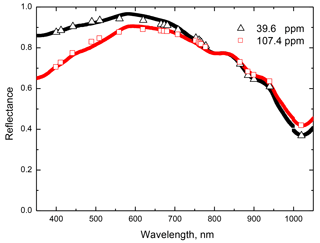
Figure 4The intercomparison of theory (symbols) with experimental measurements (line) in the European Alps ( N, E) for the polluted snowpack. The parameters R0, l, f and m have been derived from the measurements at 400, 560, 865 and 1020 nm. Reflectance measurements were collected on snow containing different concentration of dust: 39.6 ppm (black line) and 107.4 ppm (red line). The dust has been collected from the upper snow layer (≈5 cm). Snow was clean at larger depths. A complete description of this dataset is presented in Di Mauro et al. (2015).
One can see that the theory works well not only for the albedo measurements (see the previous section) but also for the reflectance measurements for polluted snow layers. In particular, our results are closer to the measurements than the theoretical model described by Flanner et al. (2007) (see Fig. 4b in Di Mauro et al., 2015). The derived parameters are given in Table 1 (lines 6–7). The value of m is 4.1 for the case with the 39.6 ppm dust concentration and 6.4 for the case with 107.4 dust concentration. Because the difference is quite large for the close locations, we conclude that snow also contained other pollutants (say, soot), and the determined value of m represents the combined effect with larger values of m for larger concentrations of dust, which is consistent with other observations of this parameter in snow (Doherty et al., 2010). The retrieved absorption coefficient of snow pollutants (at the wavelength nm) is 0.1191 m−1 for the dust concentration 39.6 ppm and 0.3123 m−1 for the dust concentration of 107.4 ppm. Assuming that the dust chemical composition and also the dust particle size distribution are the same at both locations, we can assume that the ratio of absorption coefficients at two locations should be equal to the ratio of dust concentrations. The difference between the two ratios is <3 %, which is within the measurement uncertainty (10 % for dust load measurements), suggesting that the retrieved absorption coefficients at the two sites are consistent with each other.
The mass absorption coefficient (MAC) can be estimated using
where ρ is the density of the substance of impurities. Assuming that
one can derive that
which is consistent with the values of MAC given by Utry et al. (2015) (e.g., 0.0023 m2 g−1 for quartz and 0.0051 m2 g−1 for illite; see their Table 1).
In this work, we have presented a sequence of analytical equations, which can be used to determine the snow grain size, the absorption coefficient of impurities and the absorption Ångström coefficient of surface snow impurities from the snow reflectance measured at four wavelengths: two in the visible and two in the near infrared, as suggested by Warren (2013). In the case of albedo measurements just three wavelengths can be used to find main snow properties. For unpolluted snow, it is enough to perform the measurements at two wavelengths (for reflectance measurements) or just at a single wavelength (for albedo measurements) in the near infrared to determine the snow grain size.
In principle, the refractive index of dust and dust size distribution can also be determined using derived the spectral absorption coefficient of dust and assuming the shape of dust particles. However, we did not make an attempt at such retrievals in this work. A method for the retrieval of the complex refractive index and single-scattering optical properties of dust deposited in mountain snow based on exact radiative transfer calculations was proposed by McKenzie Siles et al. (2017) under the assumption that local optical properties of dust grains can be simulated assuming the spherical shape of particles. Their method is based on the extraction of dust grains from snowpack. Our technique does not require such a complicated procedure.
We have demonstrated how snow albedo can be derived from spectral reflectance measurements avoiding complicated integration with respect to the observation geometry (azimuth, viewing angle). The last point is useful for the determination of the snow albedo from spectral reflectance measurements (say, from aircraft or satellite) at a fixed observation geometry. Although the comprehensive validation of the retrievals has not been attempted, we have found that the ratio of derived absorption coefficients of pollutants at two concentrations is close to the ratio of pollutant concentrations derived independently, which indeed should be the case taking the proximity of two measurement sites with different dust loads. The general validity of the approach is proven using field measurements (Alps, Antarctica) of both spectral reflectance and plane albedo.
The determination of the EAL l (unlike the effective grain diameter d) both from reflectance and albedo measurements is practically insensitive to the a priori unknown shape of ice crystals. Therefore, this length may be useful for the characterization of snowpack microstructure (in addition to the grain size d). The results presented in this work are useful for the interpretation of snow properties using both reflectance spectroscopy (Hapke, 2005) and imaging spectrometry (Dozier et al., 2009). It is assumed that the semi-infinite snow layer is vertically and horizontally homogeneous. The effects of the snow layer finite thickness, close-packing effects, snow vertical inhomogeneity, possible internal mixture of pollutants in snow grains and underlying surface albedo (ice, soil, grass) are ignored.
The data are available from the first author upon request.
B1 The effective absorption length and diameter of grains
Let us consider the error budget for the retrieved snow parameters. To simplify, we assume that the snow parameters are derived using albedo measurements.
The value of l is determined from measurements just at a single wavelength in the framework of the theory given above. It follows from Eq. (45) that
where
Therefore, the relative effective absorption length retrieval error is directly proportional to the relative measurement error in the measured albedo. Larger values of l correspond to the smaller albedo. So one would conclude that the error of retrieval of larger values of EAL is generally smaller (see Eq. B2). For the cases presented in Figs. 1 and 2, the wavelength 1020 nm has been used in the retrieval process, and one finds that K is equal to −2.5 and −5.8, respectively. Assuming the measurement error of 3 %, one derives that EAL is determined with accuracies of −7.5 and −17.4 %, respectively, with better accuracy for the observations in Alps, because the albedo is lower there. Also we see that the overestimation of the albedo in the experiment leads to the underestimation of the EAL, and the other way around in the of case measurements which underestimate the snow albedo because K is negative. Because K generally decreases with the wavelength, one must use the largest wavelengths to have better accuracy (say, 1020 nm instead of 865 nm). The wavelength should not be above 1200 nm or so (depending on the snow grain size) because the underlying theory is valid for weakly absorbing media only. So strong ice absorption bands must be avoided. The value of the snow grain size is proportional to the value of l. Therefore, our conclusions are also valid for the derived snow grain size assuming that one knows the parameter ξ (see Eq. 15) exactly. However, this parameter is known with some error.
The uncertainty in the parameter is difficult to access because we rely on a priori values for the snow asymmetry parameter and the absorption enhancement parameter B. We use the following values: B=1.6 and g=0.75. The reported values of g for crystalline clouds do not go above 0.8. Therefore, the modulus of the absolute error in the parameter 1−g is smaller than 0.05 (and the relative error is below 20 %). The value of B is usually in the range 1.4–1.8, and therefore the absolute error in the parameter B is equal approximately to ±0.2 and the relative error is ±12.5 %. It follows that the absolute value of the maximal relative error in the parameter ξ is close to 24 %. The error could be smaller if the assumptions used in the derivations are closer to the actual snow conditions. We find that the maximal relative error in the derived grain diameter for the cases shown in Figs. 1 and 2 is 25–30 % depending on the snow type, which is substantially larger than the error in the estimation of EAL.
Let us consider the error budget for the retrieved spectral absorption coefficient of pollutants. The absolute error of the retrieved parameter Δx is defined as
This error depends on j measurement errors of reflectance/albedo at j-channel Δyj; J is the number of channels used to retrieve the corresponding parameter assuming that there are no forward-model errors. It a difficult task to estimate the forward-model error theoretically. It depends on the specific type of snowpack.
It follows from Eqs. (46) and (B3) that
where
We conclude that the errors of the pair (f,m) determination increase if the selected wavelengths at two channels in the visible are too close and if the logarithm of albedo at selected channels is close to unity (say, weak concentration of pollutants for the channels in the visible). The albedo decreases for the cases with illumination closer to nadir. Therefore, to reduce errors, one needs to use measurements with larger deviations of Sun from the horizon direction.
The absorption coefficient of pollutants is given by the following equation (see Eqs. 8, 13, 30):
Therefore, one derives
One concludes that the errors in the estimated snow volumetric concentration c (snow density; see Appendix A), the absorption enhancement coefficient B and the pair (f,m) must be combined to estimate the total error in the retrieved spectral absorption coefficient of impurities in snow. The errors are lower if one is interested in the spectral absorption coefficient of impurities normalized to its value at a specific wavelength defined as
where λ∗ is the selected wavelength (say, 550 nm).
One derives for this coefficient
and, therefore, only the accuracy of the determination of absorption Angström exponent influences the result:
An important point is the determination of the concentration of pollutants in snow from optical remote-sensing data. In principle the concentration of pollutants can be found if the absorption coefficient of pollutants at a given wavelength is known. For instance, it follows by definition (see Eq. 31 for the definition of the volumetric absorption coefficient of impurities K) that
Therefore, uncertainty in the derived or assumed value of K (or mass extinction coefficient , where ρp is the density of the substance of a pollutant) influences the retrieval error in addition to uncertainty of the derived absorption coefficient of pollutants . One can see that the determination of the concentration of pollutants from optical remote sensing of snowpack is a very challenging task.
In particular, one finds that the positive bias in the measured albedo in the visible will lead to the underestimation of the concentration of pollutants (assuming that the grain size is exactly known). It should be pointed out that in most cases the concentration of pollutants is so small that it can not be assessed using optical instruments (change in reflectance is inside experimental measurement error). This issue has been discussed by Zege et al. (2011) and Warren (2013). Similar conclusions hold also if the reflectance (and not albedo) is the measured quantity.
AK prepared the first draft of the paper and also derived all equations presented in the paper. The measurements were performed by ML, BDM, GP, LA, MD, and FT. CB and JEB contributed to the discussion of the results and preparation of the final version of the paper.
The authors declare that they have no conflict of interest.
This work was mainly supported by the European Space Agency in the framework
of ESRIN contract no. 4000118926/16/I-NB, “Scientific Exploitation of
Operational Missions (SEOM) Sentinel-3 Snow (Sentinel-3 for Science, Land
Study 1: Snow)”. CNRM/CEN and IGE are part of LabEx OSUG@2020. Measurements
in the French Alps were funded by the ANRJCJ grant EBONI 16-CE01-0006 and at
Dome C by ANR JCJC MONISNOW 1-JS56-005-01.
Edited by: Benjamin Smith
Reviewed by: two anonymous referees
Basart, S., Pérez, C., Nickovic, S., Cuevas, E., and Baldasano, J. M.: Development and evaluation of the BSC-DREAM8b dust regional model over Northern Africa, the Mediterranean and the Middle East, Tellus B, 64, 2012, https://doi.org/10.3402/tellusb.v64i0.18539, 2012.
Belosi, F., Rinaldi, M., Decesari, S., Tarozzi, L., Nicosia, A., and Santachiara, G.: Ground level ice nuclei particle measurements including Saharan dust events at a Po Valley rural site (San Pietro Capofiume, Italy), Atmos. Res., 186, 116–126, 2017.
Di Mauro, B., Fava, F., Ferrero, R., Garzonio, R., Baccolo, G., Delmonte, B., and Colombo, R.: Mineral dust impact on snow radiative properties in the European Alps combining ground, UAV, and satellite observations, J. Geophys. Res.-Atmos., 120, 6080–6097, 2015.
Doherty, S. J., Warren, S. G., Grenfell, T. C., Clarke, A. D., and Brandt, R. E.: Light-absorbing impurities in Arctic snow, Atmos. Chem. Phys., 10, 11647–11680, https://doi.org/10.5194/acp-10-11647-2010, 2010.
Dozier, J., Green, R. O., Nolin, A. W., and Painter, T. H.: Interpretation of snow properties from imaging spectrometry, Remote Sens. Environ., 113, S25–S37, 2009.
Dumont, M., Arnaud, L., Picard, G., Libois, Q., Lejeune, Y., Nabat, P., Voisin, D., and Morin, S.: In situ continuous visible and near-infrared spectroscopy of an alpine snowpack, The Cryosphere, 11, 1091–1110, https://doi.org/10.5194/tc-11-1091-2017, 2017.
Flanner, M. G., Zender, C. S., Randerson, J. T., and Rash, P. J.: Present – day climate forcing and response from black carbon in snow, J. Geophys. Res.-Atmos., 112, D11202, https://doi.org/10.1029/2006JD008003, 2007.
Garrett, T. J.: Observational quantification of the optical properties of cirrus cloud, Light Scattering Reviews, edited by: Kokhanovsky, A., Praxis-Springer, Berlin, 3, 1–26, 2008.
Hansen, J. and Nazarenko, L.: Soot climate forcing via snow and ice albedos, P. Natl. Acad. Sci. USA, 101, 423–428, 2004.
Hapke, B.: Theory of reflectance and emittance spectroscopy, Cambridge, Cambridge University Press, 2005.
He, C., Liou, K.-N., Takano, Y., Yang, P., Qi, L., and Chen, F.: Impact of grain shape and multiple black carbon internal mixing on snow albedo: parameterization and radiative effect analysis, J. Geophys. Res., 123, 1253–1268, 2018.
Kokhanovsky, A. A. and Zege, E. P.: Scattering optics of snow, Appl. Optics, 43, 1589–1602, 2004.
Libois, Q., Picard, G., Dumont, M., Arnaud, L., Sergent, C., Pougatch, E., Sudul, M., and Vial, D.: Experimental determination of the absorption enhancement parameter of snow, J. Glaciol., 7, 714–724, 2014.
Libois, Q., Picard, G., Arnaud, L., Dumont, M., Lafaysse, M., Morin, S., and Lefebvre, E.: Summertime evolution of snow specific surface area close to the surface on the Antarctic Plateau, The Cryosphere, 9, 2383–2398, https://doi.org/10.5194/tc-9-2383-2015, 2015.
McKenzie Skiles, S., Painter, T., and Okin, G. S.: A method to retrieve the spectral complex refractive index and single scattering optical properties of dust deposited in mountain snow, J. Glaciol., 63, 133–147, 2017.
Mishchenko, M. I., Dlugach, J. M., Yanovitskij, E. G., and Zakharova, N. T.: Bidirectional reflectance of flat, optically thick particulate layers: An efficient radiative transfer solution and applications to snow and soil surfaces, J. Quant. Spectrosc. Ra., 63, 409–432, 1999.
Nazarenko, Y., Fournier, S., Kurien, U., Rangel-Alvarado, R. B., Nepotchatykh, O., Seers, P., and Ariya, P. A.: Role of snow in the fate of gaseous and particulate exhaust pollutants from gasoline-powered vehicles, Environ. Pollut., 223, 665–675, 2017.
Picard, G., Libois, Q., Arnaud, L., Verin, G., and Dumont, M.: Development and calibration of an automatic spectral albedometer to estimate near-surface snow SSA time series, The Cryosphere, 10, 1297–1316, https://doi.org/10.5194/tc-10-1297-2016, 2016.
Stamnes, K., Hamre, B., Stamnes, J. J., Ryzikov, G., Biryulina, C., Mahoney, R., Haus, B., and Sei, A.: Modeling of radiation transport in coupled atmosphere-snow-ice-ocean systems, J. Quant. Spectrosc. Ra., 112, 714–726, 2011.
Utry, N., Ajtai, T., Pintér, M., Tombácz, E., Illés, E., Bozóki, Z., and Szabó, G.: Mass-specific optical absorption coefficients and imaginary part of the complex refractive indices of mineral dust components measured by a multi-wavelength photoacoustic spectrometer, Atmos. Meas. Tech., 8, 401–410, https://doi.org/10.5194/amt-8-401-2015, 2015.
van de Hulst, H. C.: Light scattering by small particles, NY, Dover, 1981.
Warren, S. G.: Can black carbon in snow be detected by remote sensing, J. Geophys. Res.-Atmos., 118, 779–786, 2013.
Warren, S. G. and Wiscombe, W. J.: A model for spectral albedo of snow: II. Snow containing atmospheric aerosols, J. Atmos. Sci., 37, 2734–2745, 1980.
Weil, T., De Filippo, C., Albanese, D., Donati, C., Pindo, M., Pavarini, L., and Miglietta, F.: Legal immigrants: invasion of alien microbial communities during winter occurring desert dust storms, Microbiome, 5, 32, https://doi.org/10.1186/s40168-017-0249-7, 2017.
Wiscombe, W. J. and Warren, S. G.: A model for spectral albedo of snow: I. Pure snow, J. Atmos. Sci., 37, 2712–2733, 1980.
Zege, E. P., Katsev, I. L., Malinka, A. V., Prikhach, A. S., Heygster, G., and Wiebe, H.: Algorithm for retrieval of the effective snow grain size and pollutants amount from satellite measurements, Remote Sens. Environ., 115, 2674–2685, 2011.