the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Marked decrease in the near-surface snow density retrieved by AMSR-E satellite at Dome C, Antarctica, between 2002 and 2011
Nicolas Champollion
Ghislain Picard
Laurent Arnaud
Éric Lefebvre
Giovanni Macelloni
Frédérique Rémy
Michel Fily
Surface snow density is an important variable for the surface mass balance and energy budget. It evolves according to meteorological conditions, in particular, snowfall, wind, and temperature, but the physical processes governing atmospheric influence on snow are not fully understood. A reason is that no systematic observation is available on a continental scale. Here, we use the passive microwave observations from AMSR-E satellite to retrieve the surface snow density at Dome C on the East Antarctic Plateau. The retrieval method is based on the difference of surface reflections between horizontally and vertically polarized brightness temperatures at 37 GHz, highlighted by the computation of the polarization ratio, which is related to surface snow density. The relationship has been obtained with a microwave emission radiative transfer model (DMRT-ML). The retrieved density, approximately representative of the topmost 3 cm of the snowpack, compares well with in situ measurements. The difference between mean in situ measurements and mean retrieved density is 26.2 kg m−3, which is within typical in situ measurement uncertainties. We apply the retrieval method to derive the time series over the period 2002–2011. The results show a marked and persistent pluri-annual decrease of about 10 kg m−3 yr−1, in addition to atmosphere-related seasonal, weekly, and daily density variations. This trend is confirmed by independent active microwave observations from the ENVISAT and QuikSCAT satellites, though the link to the density is more difficult to establish. However, no related pluri-annual change in meteorological conditions has been found to explain such a trend in snow density. Further work will concern the extension of the method to the continental scale.
Snow density is an important variable that relates snow thickness and mass. Close to the surface, knowledge of its value is necessary to establish the surface mass balance from in situ measurements using stakes, ultrasonic sensors, ground-penetrating radar, snow pits or firn cores (Eisen et al., 2008), and satellite observations (microwave radiometer and lidar or radar altimeters, Arthern et al., 2006; Flament and Rémy, 2012; McMillan et al., 2014; Palerme et al., 2014; Markus et al., 2017). It is useful for the validation of regional climate modelling (Lenaerts and van den Broeke, 2012; Fettweis et al., 2013; Vernon et al., 2013). Surface snow density is also important to the study of the surface energy budget (Brun et al., 2011; Favier et al., 2011; Libois et al., 2013; Fréville et al., 2014), firn densification (Alley et al., 1982; Fujita et al., 2011), and air–snow exchanges (Domine et al., 2008; France et al., 2011). Its evolution is related to the local meteorological conditions, such as precipitation, wind speed, and air temperature (Brun et al., 2011; Champollion et al., 2013; Libois et al., 2014; Fréville et al., 2014). However, their links are complex and not well known. For example, snowfall can lead to different surface density behaviours depending on initial snow conditions: over hard and dense surface snow, snowfall results in a decrease in surface snow density; over surface hoar crystals, snowfall increases surface snow density. The interactions between the different meteorological effects are more complex. Wind often increases surface snow density (Sommer et al., 2018), and water vapour fluxes into the snowpack are regularly oriented towards the atmosphere, resulting in a decrease in the density near the surface. However, wind can also contribute to the sublimation of snow and thus change snow metamorphism (Domine et al., 2008).
Estimating the surface snow density in Antarctica remains difficult (Eisen et al., 2008; Groot Zwaaftink et al., 2013). It is presently not retrieved from satellite remote sensing (Groh et al., 2014), and the snow density estimates from regional climate and snowpack modelling are highly uncertain close to the surface (Brun et al., 2011; Fettweis et al., 2013). Nevertheless, Schwank and Naderpour (2018) recently presented encouraging results about the retrieval of snow density from ground-based L-band radiometry. However, this method is valid only for a soil bottom layer. In addition, despite some recent progress towards automatically measuring the snow density in the field (Mittal et al., 2009; Gergely et al., 2010), manual measurements are more accurate, with a typical accuracy around 11 % (Conger and McClung, 2009). This results in a low spatial and temporal coverage of Antarctica, especially on the East Antarctica Plateau where data are mainly acquired during traverses or close to stations (Favier et al., 2013; Groot Zwaaftink et al., 2013). Close to the surface, the measurements are more difficult and uncertain due to the surface irregularity, resulting in uncertainties higher than 11 % (Gallet et al., 2011, 2014; Champollion et al., 2013; Libois et al., 2014). Finally, an intercomparison exercise has recently shown that snow densities measured by different methods in the Swiss Alps agree within 9 % and that the vertical density variations are not completely captured (Proksch et al., 2016).
The objective of this study is to develop and validate a new method of determining the snow density near the surface from passive microwave satellite observations. The study is performed at Dome C (75∘06′ S, 123∘21′ E), on the East Antarctic Plateau, where the French–Italian base of Concordia is located, combining in situ data of snow properties and electromagnetic modelling. Except for melting regions, the method has the potential for a global spatial coverage of the Antarctic Ice Sheet, which will be addressed in further work. Following Brucker et al. (2011), we first simulate the snow microwave emission and thus quantify its sensitivity to snow properties. Qualitatively, it is well known that the permittivity of snow is highly dependent on density (Mätzler et al., 1984; Warren and Brandt, 2008) and thus changes in the different layers of the snowpack. The electromagnetic reflections at each interface between layers with different densities (air–snow or internal snow–snow interfaces) are calculated with Fresnel equations that use the snow permittivity and depend on the polarization (Born and Wolf, 1999). As a consequence, snow density greatly influences the polarization of microwave radiation, which was noted in previous studies (Shuman et al., 1993; Shuman and Alley, 1993; Abdalati and Steffen, 1998; Liang et al., 2009; Champollion et al., 2013; Brucker et al., 2014; Leduc-Leballeur et al., 2015, 2017). Using the Dense Media Radiative Transfer - Multi Layers model (DMRT-ML, Tsang et al., 2000a; Roy et al., 2012; Picard et al., 2013; Dupont et al., 2013), we quantitatively determine the influence of surface snow density on microwave polarization ratio. This relationship is then used to retrieve the density from satellite observations, which are measured by the Advanced Microwave Scanning Radiometer – Earth observing system (AMSR-E) instrument. In situ measurements of snow properties are used as input for the DMRT-ML model. Active microwave observations and in situ measurements of surface snow density are used to validate the method.
Section 2 presents remote sensing and in situ data and the microwave emission model. Section 3 presents some elements of the theoretical background of microwave radiative transfer, and Sect. 4 presents the method of retrieving the surface snow density. Section 5 presents the time series of the retrieved surface snow density and its validation and analysis.
Satellite remote sensing datasets, measurements of snow properties, and the microwave radiative transfer model are described in the three following sections.
2.1 Satellite observations
2.1.1 Passive microwave data
Passive microwave satellite observations were acquired at 18.7 and 36.5 GHz by the AMSR-E instrument on-board the Aqua satellite in dual-polarization mode with an observation zenith angle of 54.8∘ over the entirety of the instrument's lifetime, i.e. from 18 June 2002 to 4 October 2011. Daily averaged brightness temperatures (TB) at Dome C are extracted from the “AMSR-E/Aqua Daily L3 25 km Brightness Temperature & Sea Ice Concentration Polar Grids, Version 3” provided by the National Snow and Ice Data Center (NSIDC, Cavalieri et al., 2014). The pixel size is 25 km × 25 km and the total sensor error is around 0.6 K. The dataset contains, for every day, the mean of the daily averaged ascending orbits and daily averaged descending orbits. This typically represents seven overpasses per day at Dome C.
A detailed analysis of the spatial and temporal variability of passive microwave data close to Dome C is given by Long and Drinkwater (2000), Macelloni et al. (2007), Picard et al. (2009), and Brucker et al. (2011). As in these previous studies, we assume that (1) only one or a few in situ measurements are sufficient to model the brightness temperature of an entire satellite pixel and (2) the pixel containing in situ measurements is representative of the satellite pixels around Dome C. These assumptions have been validated using ground-based radiometers by Picard et al. (2014), who found that the Dome C area was sufficiently homogeneous.
2.1.2 Active microwave data
Two complementary datasets of active microwave observations are used for comparison with the retrieved snow density. The first dataset was acquired by the nadir-looking Radar Altimeter 2 (RA-2) instrument on-board the ENVIronment SATellite (ENVISAT) at 13.6 GHz (Ku band). The dataset contains the total backscatter power from 12 March 2002 to 8 April 2012 based on along-track data and the Ice-2 retracking algorithm (Legrésy et al., 2005; Rémy et al., 2014). Radar backscatter corresponds to the ratio between the energy emitted by the satellite and the energy reflected by the snow surface and is expressed in decibels. Due to the 35 days of ENVISAT revisit time and the selection of four orbit tracks that are less than 17 km away from Concordia station, temporal sampling of RA-2 observations is typically 8–10 days. The along-track spatial sampling over the Antarctic Ice Sheet is 330 m, and its typical footprint is of the order of 5–10 km (Rémy and Parouty, 2009). The sensor precision for determining surface elevation is 47 cm.
The second dataset of active microwave observations was acquired by the SeaWinds instrument on-board the Quick SCATterometer (QuikSCAT) at 13.4 GHz in dual-polarization mode. Zenith viewing angles are 46 and 54.1∘ for horizontal and vertical polarizations, respectively. Normalized radar cross sections σ0 were extracted at Dome C from the “egg images of SeaWinds on QuikSCAT Enhanced Spatial Resolution Image Sigma-0 Products – version 2” provided by the National Aeronautics and Space Administration – Scatterometer Climate Record Pathfinder (http://www.scp.byu.edu/data/Quikscat/SIRv2/Quikscat_sirV2.html, last access: 8 April 2019, Long and Daum, 1998; Early and Long, 2001; Long et al., 2001). The pixel size is 2.225 km × 2.225 km and the relative error is 0.2 dB (Spencer et al., 2000; Early and Long, 2001). The dataset contains the daily averaged backscatter coefficient by combining multiple passes of QuikSCAT (near-polar orbit) from 19 July 1999 to 23 November 2009.
2.2 In situ snow measurements
Snow observations include the snow density near the surface and the vertical profiles of snow temperature, density, and specific surface area (SSA).
2.2.1 Surface snow density
Three time series of snow density were measured at Dome C. The first set of measurements is from the CALVA programme (CALibration-VAlidation of climate models and satellite retrieval, Antarctic coast to Dome C). Surface snow density was measured every 3 to 5 days from 3 February 2010 to 4 October 2011 by using a cylinder cutter (10 cm length and diameter of 5 cm) inserted horizontally so that the cutter top grazes the surface. The value used here is the average of three measurements. The two other sets of measurements are from the project MAPME (Monitoring of Antarctic Plateau by means of Multi-Frequency Microwave Emission) funded by PNRA (Programma Nazionale di Ricerche in Antartide). The second dataset contains the snow density measured from 9 May 2008 to 4 October 2011 by using a cylinder cutter of 25 cm height and a diameter of 4.5 cm. Measurements were performed at 0.1 m depth every 15 days in a snow stake network composed of eight poles placed 10 m apart . The value used here is the average of eight measurements. The last dataset contains the snow density measured in snow pits, which were excavated every month from 18 December 2007 to 4 October 2011. Density values were collected every 10 cm in the 0–1 m depth range. A single measurement was collected at each depth of the snow pit.
The mean density value is 329, 344, and 321 kg m−3, respectively, for the CALVA dataset and the two PNRA datasets. The standard deviation is, respectively, 43, 40, and 54 kg m−3. The density is representative of the topmost 5 cm of the snowpack for the CALVA dataset and of the top 10 cm for the two PNRA datasets. Uncertainties associated with the three datasets are equal to or higher (due to the low cohesion of surface snow) than the uncertainty estimated for classic density measurements (11 %, Conger and McClung, 2009).
For the first time, the spatial variability of surface snow density measurements has been assessed with three series of 40 measurements (measurements taken every 1, 10, and 100 m). The averages and standard deviations are, respectively, 298.7±29.3, 317.6±24.7, and 307.9±59.8 kg m−3 for metre, decametre, and hectometre scales. Considering all measurements (n=120), we found a mean density and standard deviation of 308.3±41.6 kg m−3. Under the assumption of a normal distribution of snow density measurements, the value 83.2 kg m−3 covers 95 % of the distribution variance. This value represents 26.9 % of the mean density and is assumed to represent the spatial variability of surface snow density measurements around Dome C. We also assume that there were no changes in the spatial variability during the study period (2002–2011).
2.2.2 Snow temperature profile
Snow temperature was recorded every hour from 1 December 2006 to 4 October 2011 and from the surface to 21 m depth, with 35 probes initially installed every 0.1 m down to 0.6 m depth, every 0.2 m down to 2 m, every 0.5 m down to 5 m, and every 1 m down to 21 m. The probes are located around 1 km west of the Concordia station. All probes (100 Ω platinum resistance sensors with an accuracy better than ±0.1 K at 223 K) were inter-calibrated with a precision of ±0.02 K. The probes are continuously being buried over time due to snow accumulation, which is estimated to be around 0.1 m yr−1 (Frezzotti et al., 2005, 2013; Arthern et al., 2006; Eisen et al., 2008; Brucker et al., 2011; Verfaillie et al., 2012). Initial probe depths are corrected as a function of the date measurements. In addition, the temperature measurements closest to the surface become deeper and deeper over time. This means that no measurements are taken in the upper snowpack. To correct for this issue, we extrapolate the profiles using an exponential function between the uppermost probe in the snowpack and the temperature at the surface (Picard et al., 2009; Brucker et al., 2011; Groot Zwaaftink et al., 2013). The latter is approximated by the 2 m air temperature. Air temperature was extracted from the global ERA-Interim reanalysis provided by the European Centre for Medium-range Weather Forecasts (ECMWF, Dee et al., 2011), which is considered the superior reanalysis in the East Antarctica region (Xiie et al., 2014). We use passive microwave observations that are daily, which is why we calculate daily averaged temperature by averaging two hourly profiles (14:00 and 00:00 LT).
2.2.3 Snow density profile
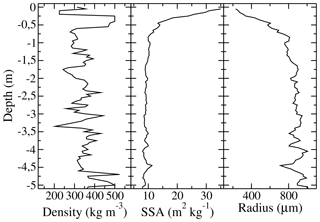
The snow density profile (Fig. 1) is considered constant and is composed of two different datasets. The first dataset was measured in January 2010 by determining the mass and volume of snow and firn core samples every 5 cm, collected up to 20 m depth. However, the cohesion of the first 0.3 m of the snow core was very low and impossible to sample correctly. Thus, a second dataset was measured in December 2010 to complete the snow density profile from the surface down to 0.3 m depth. This second dataset is an average of 13 short density profiles (up to 0.5 m depth) measured in a snow pit with a dedicated cutter for Antarctic snow (Gallet et al., 2011).
The snow core and snow pit density profiles below 0.3 m depth are close together. Indeed, the mean and standard deviation of both profiles (0–0.5 m deep) are about 340 ± 8 kg m−3 for the snow core dataset and about 355 for the snow pit dataset. In addition, the overlapping part (between 0.3 and 0.5 m depth) shows similar values. Uncertainties associated with both methods are similar: at least 10 % for measurements of snow and firn core samples (Arthern et al., 2010) and at least 11 % for snow cutter measurements in a snow pit (Conger and McClung, 2009).
2.2.4 Snow-specific surface area profile
The snow SSA (Fig. 1) is the surface area of ice crystals divided by the mass of snow (Domine et al., 2006; Arnaud et al., 2011). Its profile up to 20 m depth was measured in January and December 2010 using the Profiler Of Snow-Specific Surface area Using short-wave infrared reflectance Measurement instrument (POSSSUM, Arnaud et al., 2011) and the Alpine Snow Specific Surface Area Profiler (ASSSAP, Champollion, 2013; Libois et al., 2014), which is a lightweight version of POSSSUM adapted for shallow snowpacks (maximum 2 m deep). These two instruments are based on the relationship between snow reflectance in the near-infrared domain and snow SSA (Domine et al., 2006; Matzl and Schneebeli, 2006). Using a laser at 1310 nm illuminating the face of a snow hole and a specific data processing algorithm (Arnaud et al., 2011), POSSSUM and ASSSAP instruments determine the snow SSA as a function of depth in the field. Uncertainty associated with SSA measurements from POSSSUM is about 10 % (Arnaud et al., 2011). Both instruments are very similar and have been compared multiple times, thereby ASSSAP uncertainty is considered to be 10 % as well.
Larger errors were found above 0.3 m depth using POSSSUM than when using ASSSAP. Thus, we decided to use SSA measurements from ASSSAP for the first 0.3 m and POSSSUM observations below. SSA profiles from both instruments overlap between 0.3 and 0.5 m depth and show very close values. Averaged SSA values from ASSSAP are 13.2 and 13.9 m2 kg−1 for POSSSUM. Due to an artefact that increases the measured SSA when the hole is drilled for snow below 5 m (Picard et al., 2014), we removed the measured values and replaced them with a constant value (SSA5 m). This value is optimized following Brucker et al. (2011) (Sect. 5.1).
The snow SSA is not directly used in DMRT-ML model. The snow parameter that characterizes the snow grain size in the electromagnetic model (rDMRT-ML, Fig. 1) is related to the optical radius (ropt). The relationships between snow SSA, DMRT-ML radius, and optical radius are given by the following equations:
where ϕ is a snow microstructure parameter that depends on the shape of snow crystals and the stickiness and size distribution of ice crystals (Brucker et al., 2011; Roy et al., 2012; Dupont et al., 2013) and ρice is the density of ice, i.e. 917 kg m−3. The ϕ parameter is optimized as in Brucker et al. (2011) (Sect. 5.1).
2.3 Microwave emission model
2.3.1 Snow microwave emission
The snow microwave emission model DMRT-ML (Picard et al., 2013) has already been applied and validated in several studies (Brucker et al., 2011; Roy et al., 2012; Dupont et al., 2013; Picard et al., 2014) and is freely available (http://pp.ige-grenoble.fr/pageperso/picardgh/dmrtml/, last access: 8 April 2019). It allows the computation of the top-of-snowpack emerging brightness temperature for a given snowpack at different viewing angles, at different frequencies, and at both vertical and horizontal polarizations. The model is composed of two parts: (1) the DMRT theory to calculate the absorption and scattering coefficients for all snow layers – in the model, the snowpack is composed of horizontally semi-infinite and vertically homogeneous snow layers of dense ice spheres, completely defined by the layer thickness, temperature, density, and optical radius of snow – and (2) the DIScrete Ordinate Radiative Transfer method (DISORT, Jin, 1994) to propagate the thermal emission of each snow layer from the bottom of the snowpack to the atmosphere. DISORT accounts for multiple scattering between layers. Layers are assumed to be planes, parallel, and much thicker than the wavelength.
We use the model in a non-sticky grain configuration, i.e. grains which do not form aggregates, and with a unique optical radius of snow grains, i.e. no grain size distribution. Snow crystal aggregates are not considered in this study because the ϕ parameter used to convert snow SSA into an optical radius partly integrates this snow property (Roy et al., 2012; Löwe and Picard, 2015). We also use a semi-infinite bottom snow layer to consider the firn of the Antarctic Ice Sheet. In addition, two criteria must be respected in the framework of DMRT theory: snow density less than 300–350 kg m−3 (Liang et al., 2006; Tsang et al., 2008) and low optical radius with respect to the wavelength (Rayleigh scattering). The latter is always respected in our study since rDMRT-ML never exceeds 0.6 wavelengths and most of the time is lower than 0.1. Regarding when the density is sometimes higher than 350 kg m−3 in our profile (Fig. 1), Picard et al. (2013) explained that the deviation in scattering and absorption coefficients remains moderate.
2.3.2 Atmospheric contribution
The atmosphere attenuates the microwave emissions emerging from the surface and itself emits microwaves due to its own temperature (Rosenkranz, 1992). Although this effect is low over the Antarctica Plateau because of the low atmospheric humidity and the small size of scatterers in the atmosphere (Walden et al., 2003; Genthon et al., 2010), both effects are taken into account in our modelling on a daily basis with a simple non-scattering radiative transfer scheme. Top-of-atmosphere (TOA) brightness temperatures are computed using the method and equations from Rosenkranz (1992) and following Picard et al. (2009). Upward and downward atmospheric TB's are calculated using atmospheric temperature and moisture profiles from ERA-Interim reanalysis. The transmission coefficient is 0.960 at 37 GHz and 0.987 at 19 GHz, and the downward cosmic TOA TB is 2.75 K.
Some elements of the theoretical background of microwave satellite remote sensing are described in the next two sections.
3.1 Passive microwave remote sensing
We use the brightness temperature polarization ratio (PR) at 19 and 37 GHz to increase the sensitivity of passive microwave observations to surface properties (Shuman et al., 1993; Surdyk, 2002a; Champollion et al., 2013):
where TB(ν,α) is the brightness temperature, ν the frequency, and α the polarization.
Champollion et al. (2013) showed that PR, at the AMSR-E incidence angle, which is close to the Brewster angle for the air–snow interface, mainly depends on the snow density near the surface, the surface roughness, and the vertical snow stratification, i.e. abrupt changes in the snow density profile. We consider flat interfaces that neglect the influence that roughness has on PR (the relevance of this assumption is explained in Sect. 5.5). Consequently, the polarization ratio is a non-linear combination of surface and internal reflections (Leduc-Leballeur et al., 2017).
In order to understand the polarization ratio evolution, two cases are explored: (1) snow properties that vary with depth but are constant in time and (2) snow properties that also vary over time. For case (1), the PR evolution is only due to changes in the snow density near the surface. For case (2), PR evolution is also influenced by changes in the snow density stratification. Snow evolution is mainly influenced by atmospheric conditions. The surface is first affected and then atmospheric influence diffuses deeper into the snowpack. This process is slow on the Antarctica Plateau (Surdyk, 2002b; Brucker et al., 2011; Picard et al., 2014; Libois et al., 2014) and implies a slower evolution of snow deeper into the snowpack than near the surface. As a result, the PR evolution is primarily influenced by surface snow density variations (the relevance of this assumption is explained in Sect. 5.5).
3.2 Active microwave remote sensing
The signal returned by the snowpack is a complex combination of surface and volume scattering (Rémy and Parouty, 2009; Rémy et al., 2014; Tedesco, 2015; Adodo et al., 2018). The surface-to-subsurface signal ratio is used to determine the main contributor to radar backscatter observations. On the East Antarctica Plateau this ratio is high (Lacroix et al., 2008, 2009), and thus surface echo is the main contributor to the radar backscatter at Dome C. Consequently, the long-term evolution of ENVISAT observations mainly depends on surface snow density and roughness.
Because the incidence angles of the SeaWinds instrument are close to the Brewster angle for the air–snow interface, the surface reflection at vertical polarization is weakly influenced by the near-surface snow density. Consequently, the evolution of the radar backscatter coefficient at vertical polarization is mostly dependent on surface roughness changes. Therefore, considering the independence of volume scattering from the polarization (Tsang et al., 2000b; Picard et al., 2013), as well as the independence of surface roughness effect from the polarization (Ulaby et al., 1982; Adodo et al., 2018), we defined the radar polarization ratio (RPR) to be primarily influenced by the snow density near the surface (Liang et al., 2008):
where σ0 is the radar backscatter coefficient, r0 is the part of backscatter coefficient considering only the surface reflection, and h and v are the polarizations. For simplicity, the ν index is not written.
The different steps of the method of retrieving the surface snow density are described in this section. Surface density variations are deduced from the PR evolution. However, to correctly simulate PR evolution, we first need to simulate the mean state of the PRs.
-
In the first step, we follow the forward modelling approach of Brucker et al. (2011) to simulate the time series of brightness temperatures, using the vertical profiles of snow properties, which, except for the temperature, are kept constant over time. From the simulated brightness temperatures, we calculate the time series of polarization ratios and show the correct simulation of the mean polarization ratios and the poor modelling of their temporal variations.
-
In the second step, we simulate the polarization ratio variations due to changes in the properties of a 0.03 m snow layer on top of the snowpack theoretically (as in Leduc-Leballeur et al., 2015, 2017), and we also show the strong relationship between PR at 37 GHz and the density of this surface layer.
-
The third step corresponds to the retrieval algorithm itself. We estimate the time series of surface snow density by minimizing the deviations between the modelled and observed polarization ratio at 37 GHz.
Some studies have reported high vertical snow stratification around Dome C (Gallet et al., 2014; Picard et al., 2014). They observed very dense and thick snow layers (about 500 kg m−3 for 0.3–0.5 m thick), and thin and low-density layers (less than 150 kg m−3 for a thickness of few centimetres). The poor modelling of the horizontally polarized brightness temperature could be due to an underestimation of the snow stratification (Macelloni et al., 2007; Brucker et al., 2011; Champollion et al., 2013; Picard et al., 2013; Leduc-Leballeur et al., 2015). In order to correctly simulate the mean horizontally polarized brightness temperatures, and thus the mean polarization ratios, we added, at 0.1 and 0.2 m depth in our snow density profile, two layers that were 0.1 and 0.2 m thick with a density equal, respectively, to 225 and 500 kg m−3.
The results of the different steps to retrieve the surface snow density are presented in the next three sections. The fourth section is dedicated to the comparison and validation of the retrieved density, and the last section examines the different sources of uncertainties.
5.1 Time series simulation
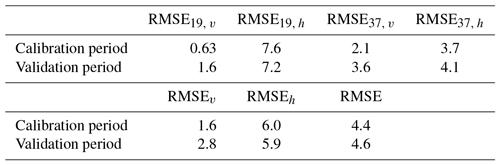
TOA horizontally and vertically polarized brightness temperatures at 19 and 37 GHz – written TB(19, V), TB(19, H), TB(37, V) and TB(37, H) – are simulated with the DMRT-ML model during the 3 years (from 1 December 2006 to 31 December 2009) when the temperature profiles were recorded. The two parameters SSA5 m and ϕ are optimized during this period of calibration by minimizing the root-mean-square error (RMSE) between the modelled and observed TB(19, V) and TB(37, V). As in Brucker et al. (2011), only the vertical polarization is used because of its high sensitivity to snow SSA and reduced sensitivity to density changes. TOA brightness temperatures are then simulated over nearly 2 years of validation (from 1 January 2010 to 4 October 2011) using the optimized SSA5 m and ϕ parameters. RMSEs are defined by the following equations:
where n is the number of observations, and the observed and modelled brightness temperatures at ν frequency α polarization, and p=4 the number of polarizations and frequencies used.
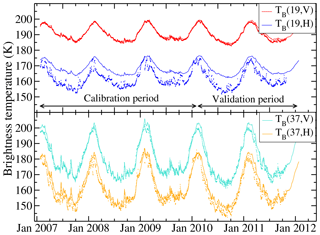
Figure 2Time series of modelled (lines) and observed (dots) brightness temperatures, at 19 and 37 GHz and at vertical and horizontal polarizations – TB(19, V), TB(19, H), TB(37, V) TB(37, H) – at Dome C, Antarctica, during the calibration period (2007–2009) and the validation period (2010–2011).
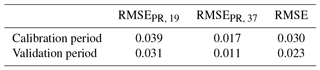
The time series of observed and modelled brightness temperatures are shown in Fig. 2. The optimized SSA5 m and ϕ parameters are, respectively, equal to 10.1 m2 kg−1 and to 2.5, which is in the range of those found by Brucker et al. (2011) and Picard et al. (2014), respectively, 2.8 and 2.3, with an RMSE of 1.6 K. Observed brightness temperatures are well reproduced by the DMRT-ML model both in terms of absolute value and evolution, except for 19 GHz at horizontal polarization. The RMSE calculated by excluding TB(19, H) is indeed 2.6 K, whereas RMSE 19, h is 7.4 K. Table 1 summarizes all errors between observed and modelled TB's. The RMSE during the calibration and validation periods are very close, showing the high performance of the optimization. We also found a slight improvement in the modelled TB(19, H) compared to Brucker et al. (2011) with an RMSE 19, h of 7.4 K instead of 8–10 K. These results confirm the representativeness of the in situ measurements for the satellite pixel encompassing Dome C (25 km × 25 km).
Table 1Errors between modelled and observed brightness temperatures (K) for the calibration and validation periods.
The polarization ratio evolution, calculated from the simulated brightness temperatures, does not reproduce the observed variations, and the 5-year average of modelled PR19 overestimates the observations by 0.033 (Fig. 3). This represents around 46 % of the maximum amplitude of observed PR19 variations. On the other hand, mean PR37 is well modelled. The simulated mean PR37 is indeed 0.904, whereas the observed mean PR37 is 0.896. The difference represents only 11 % of the maximum amplitude of observed PR37 variations. Table 2 summarizes all errors between observed and modelled PRs.
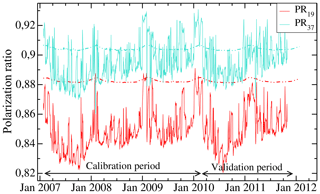
Figure 3Time series of modelled (lines) and observed (dots) polarization ratios at 19 and 37 GHz (PR19 and PR37) at Dome C, Antarctica, during the calibration period (2007–2009) and the validation period (2010–2011).
The poor simulation of the mean PR19 comes from an incorrect simulation of TB(19, H) which, as explained in Arthern et al. (2006), is mainly due to the stratification of the snowpack. Because PR37 is well reproduced, and considering that penetration depth is, respectively, around 5 and 1 m for 19 and 37 GHz (Surdyk, 2002b), the stratification in the first metre of the snowpack is adequately represented. Hence, the discrepancy between observed and modelled PR19 is probably because of a stratification that is too weak below 1 m depth, and further works can address this issue by increasing the stratification deeper into the snowpack. The poor simulation of the mean PR19 is not a major issue in this work since we study the time variations in polarization ratios. However, we decided to exclude 19 GHz data frequency in the following in order to avoid introducing bias in the retrieved density.
Table 2Errors between modelled and observed polarization ratios for the calibration and validation periods.
In contrast to the long-term average, the seasonal and faster variations in the polarization ratio at 37 GHz are not reproduced. We explain this by the fact that the evolution of polarization ratio is mainly governed by variations in the snow density close to the surface, whereas we have considered the snow density profile constant over time in our simulation here.
5.2 Sensitivity analyses
In order to represent the snow evolution close to the surface and thus to simulate PR37 variations, a thin layer (0.03 m thick) is added on the top of the previous snowpack. Then a sensitivity analysis of PR37 to the snow parameters of this top layer is performed using the DMRT-ML model. The PR37 variations that occur due to changes of a single snow parameter of the upper layer (density, temperature, SSA or thickness), by keeping the other variables constant (equal to those of the next layer), are shown in Fig. 4. The simulations are performed for two temperature profiles corresponding to typical summer and winter conditions (1 January and 1 August).
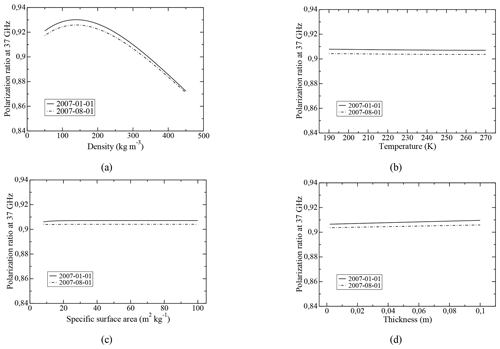
Figure 4PR37 variations caused by changes in the snow properties of the top layer: (a) density, (b) temperature, (c) SSA, and (d) thickness. The two different dates correspond to typical winter and summer temperature profiles.
The results clearly show that only the density of the first layer can significantly change the polarization ratio. For comparison, large variations in SSA from 10 to 100 m2 kg−1, thickness from 0.01 to 0.1 m, and temperature from 190 to 270 K result in small changes of PR37 (respectively, around 2 %, 5 %, and 1.5 % of the PR variations are caused by density changes from 150 to 450 kg m−3). In addition, variations in snow density between 150 to 450 kg m−3 simulate all of the observed range of temporal PR variations between 0.88 and 0.92. Moreover, this simulation shows the weak influence of the temperature profile on polarization ratio. The larger variation due to the different temperature profiles is 0.0043, which represents only 7.25 % of the larger PR variation caused by surface density changes (from 150 to 450 kg m−3). This sensitivity analysis demonstrates the strong relationship between the polarization ratio at 37 GHz and surface snow density and thus shows the possibility of retrieving the density ρsat from the PR37 satellite observations.
5.3 Surface snow density evolution
Surface snow density ρsat is estimated every day by minimizing the RMSE between the observed and modelled PR37 and only changing the snow density of the top layer. The RMSE minimization is done though a Newton approach (scipy.optimize.newton function of Python). This method ensures a quick convergence (typically after 3–5 iterations) with a residual RMSE less than 0.001. That translates into a precision of surface snow density equal to 3.5 kg m−3. We use a constant vertical profile of temperature equal to the 5-year average of the vertical temperature profile measured in the field. This choice is motivated by the fact that no temperature data are available before December 2006. However, the results are weakly affected by this assumption (Sect. 5.5). Because of the 5-year average, the temperature profile is also nearly constant with depth around 218.5 K, which is the mean annual temperature at Dome C between 2006 and 2011 (periods where temperature measurements are available). The SSA and the thickness of the top snow layer are 60.0 m2 kg−1 and 30 mm, respectively (Champollion, 2013; Libois et al., 2015; Leduc-Leballeur et al., 2017). The retrieved density is approximately representative of the mass of snow integrated over 3 times the wavelength, which corresponds to around the top 3 cm of the snowpack (Ulaby et al., 1981, 1982; Tsang et al., 2000b), the wavelengths of AMSR-E being 8.2 mm at 37 GHz in the air. This representativeness can change slightly (between 2 and 5 cm) depending on the type of crystals present on the surface (Leduc-Leballeur et al., 2017).
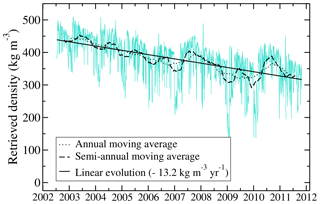
Figure 5Time series of the snow density near the surface ρsat at Dome C, Antarctica, retrieved from AMSR-E passive microwave observations and covering the period from 18 June 2002 to 4 October 2011.
The time series of ρsat from 18 June 2002 to 4 October 2011 shows fast and large variations, an annual cycle and a pluri-annual decrease trend (Fig. 5). The fast variations have a maximum amplitude of about 200 kg m−3 for a typical timescale of few days and are certainly linked to wind and precipitation, which are frequent atmospheric processes with a potentially large impact on snow density (Picard et al., 2012; Champollion et al., 2013; Libois et al., 2014; Brucker et al., 2014; Leduc-Leballeur et al., 2017). Hoar formation on the surface, for a typical duration of 1 week, can also greatly impact surface snow density (Champollion et al., 2013).
The annual cycles have a mean amplitude of about 30 kg m−3, using two extreme years (2007 and 2010, when the amplitude reached nearly 60 kg m−3) that correspond to two summers with low accumulated precipitation and a large increase in the snow grain size in the first 5 cm of the snowpack (Picard et al., 2012). These conditions probably involve intense metamorphism of the snow near the surface during the summer and can potentially result in a longer presence of hoar crystals on the surface or larger hoar crystals (Champollion et al., 2013) that decrease surface snow density (Gallet et al., 2014). The year 2008 is also peculiar, due to its lack of an annual cycle.
A pluri-annual decrease trend of −13.2 kg m−3 yr−1 is observed over the 10 years of AMSR-E observations. This evolution represents a significant change and could result from an increase in precipitation (recent snow being usually less dense than old snow), a decrease in wind speed (wind usually compacts surface snow), or a longer and more frequent presence of hoar and sublimation crystals on the snow surface (hoar and sublimation crystals usually being less dense than small rounded grains, Domine et al., 2006).
5.4 Comparison and validation
5.4.1 Comparison with in situ measurements
Figure 6 shows the time series of ρsat and the three time series of the in situ surface snow density. We obtain a remarkable agreement even if different daily and weekly variations are observed. The range of observed density is 150–425 kg m−3 for in situ measurements and satellite estimation during the overlap period. From February 2010 to October 2011 (when all datasets are available), the mean surface snow density is 339.8±58.8, 304.2±48.7, 346.4±43.9 and 303.4±57.6 kg m−3, respectively, for the satellite, CALVA measurements, PNRA stake, and PNRA pit measurements. The datasets are consistent with one another and the mean values are within the uncertainty range. However, we observe three notable differences: (1) measurements in snow pits are regularly lower by 35–40 kg m−3 than satellite and stake estimates, (2) spatial variability of snow density (41.6 kg m−3) is of the same order of magnitude as the differences between the mean value of datasets (higher difference is 43 kg m−3), and (3) satellite density (standard deviation is 63.5 kg m−3) is generally more variable than the in situ measurements (standard deviations are 43, 40, and 54 kg m−3). The last observation (3) could be the result of the approximative thickness of the retrieved satellite surface snow density (2–5 cm) compared with the in situ measurements (about 5 cm for CALVA measurements and 10 cm for PNRA measurements).
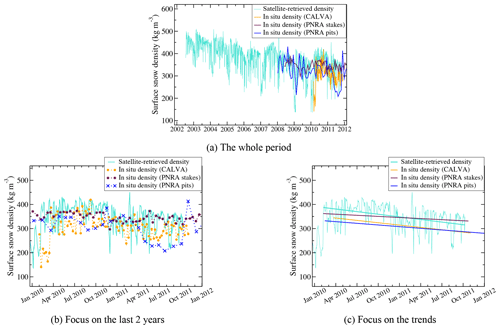
Figure 6Time series of the snow density near the surface at Dome C, Antarctica, retrieved from AMSR-E passive microwave observations and measured in the field (three different datasets) from 18 June 2002 to 4 October 2011 (a). Panel (b) focuses on the last two years, and panel (c) focuses on the trends during the last two years.
The four time series of surface snow density show a pluri-annual decreasing trend. The linear trends during the common period (February 2010 to October 2011) for the four time series are of the same order of magnitude, between −20 and −40 kg m−3 yr−1. The trend over 10 years of the satellite-retrieved density is −13 kg m−3 yr−1 and the trend over 4 years of the two PNRA in situ datasets are −6 and −8 kg m−3 yr−1.
5.4.2 Comparison with existing studies
Gallet et al. (2014) measured the snow density very close to the surface and found a range of density between 125 and 165 kg m−3 for the first centimetre of snow and between 202 and 290 kg m−3 for the second centimetre. In Gallet et al. (2011), the authors sampled the density near the surface in snow pits (at around 2 cm depth) and found a snow density range from 146 to 325 kg m−3. Libois et al. (2014) measured the snow density near the surface between 150 and 360 kg m−3. In a study dedicated to spatial variability, Picard et al. (2014) found a range of snow density from 270 to 520 kg m−3 in the first metre of the snowpack. During the 2010–2011 summer campaign at Dome C, we measured surface snow densities between 270 and 380 kg m−3. We also measured the density of hoar crystals present at the surface. The mean value was 178 kg m−3, in agreement with the measurements of hoar crystal density performed in Greenland of 150 kg m−3 (Shuman et al., 1993). All surface snow density measurements are coherent together, showing lower density values when surface snow is covered by hoar crystals (about 125–178 kg m−3). The surface snow densities retrieved from satellite are between 136 and 508 kg m−3. The average density over the 10 years is 377 kg m−3 and the standard deviation is 63.5 kg m−3. The retrieved densities are slightly higher than those found in existing studies or those measured during the 2010–2011 summer campaign (upper bound is 380 kg m−3). The average of ρsat is close to the mean density of the first 3–5 m of snow at Dome C, which is about 350–360 kg m−3 with a range between 250–260 and 480–490 kg m−3 (Frezzotti et al., 2005; Brucker et al., 2011; Verfaillie et al., 2012; Groot Zwaaftink et al., 2013). The time series of ρsat shows a large range of density and all its values have frequently been observed in previous field studies.
Champollion et al. (2013) linked the presence of hoar crystals on the snow surface and passive microwave observations. We reassess this former study here by examining the variations in the retrieved density during hoar formation and disappearance events from 23 November 2009 to 4 October 2011. Among the 14 hoar formation events observed with an automatic camera in the field, ρsat decreases in 10 of them, with an average amplitude of −49.0 kg m−3 in a single day. For the four remaining events, ρsat slightly increases by 15.0 kg m−3; for the 15 hoar disappearance events observed from the ground, ρsat increases as expected for 14 of them, with an average amplitude of +47.0 kg m−3; for the remaining event, ρsat decreases by −10.0 kg m−3. The good agreement between the quick ρsat variations and hoar evolution confirms the precision of the detection of density changes from AMSR-E. The influence of surface properties on passive microwave observations has also been confirmed in Brucker et al. (2014) and Leduc-Leballeur et al. (2017).
5.4.3 Comparison with active microwave observations
The QuikSCAT 7-year time series of the residual backscatter at vertical and horizontal polarization and the radar polarization ratio are shown in Fig. 7. The time series are smoothed with a 5-day moving window in order to reduce the influence of the QuikSCAT viewing angle variations. The three curves feature quick variations (daily to monthly), an annual cycle (clearly visible only after 2004 for RPR time series), and a pluri-annual trend. The linear trend of vertical polarized backscatter is nearly constant, whereas the time series of horizontal polarization backscatter shows a linear decrease of −0.03 dB yr−1. The RPR time series increases by 0.0042 yr−1, which is comparable to the observed trends of passive microwave observations: 0.0032 yr−1 for PR37, 0.0033 yr−1 for PR19, and 0.0024 yr−1 for PR10. We can conclude from the absence of a trend in the time series that surface roughness has not evolved much between 2002 and 2009 at Dome C, Antarctica. Furthermore, the negative trend of the horizontal backscatter and the positive trend of RPR are certainly associated with a slow decrease in surface snow density since 2002, and thus QuikSCAT observations confirm the density retrieved from AMSR-E satellite.
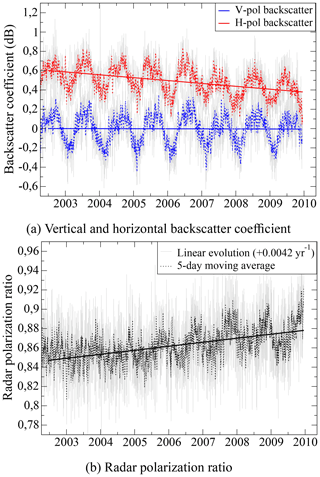
Figure 7Time series of the residual vertical and horizontal backscattering coefficients and the radar polarization ratio from QuikSCAT at Dome C, Antarctica, from 18 June 2002 to 23 November 2009. Grey lines are the original data and red, blue, and black dots are the 5-day moving averages. Note the different vertical axis scales for horizontal polarization (H-pol) and vertical polarization (V-pol)
The ENVISAT–RA-2 time series of the residual backscatter at 13.6 GHz is presented in Fig. 8. The time series shows a superimposition of a negative linear trend of −0.1 dB yr−1, an annual cycle with large amplitude (between 0.4 and 1.2 dB yr−1), and weekly oscillations. These latter variations are residual biases between ascending and descending passes and are removed by smoothing the time series. The annual cycles are caused by changes in the volume echo of the ENVISAT observations (Adodo et al., 2018).
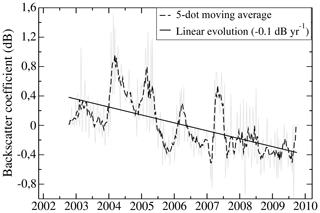
Figure 8Time series of the backscattering coefficient from ENVISAT–RA-2 at Dome C, Antarctica, from 12 March 2002 to 8 April 2012.
The pluri-annual trend of ENVISAT–RA-2 observations of −0.1 dB yr−1 comes mainly from a progressive evolution of surface snow density or surface roughness (Sect. 3.2). Lacroix et al. (2008, 2009) quantified the influence of individual snow parameters on radar backscatter by modelling the waveform of the altimetric signal. We use the relationship found by Lacroix et al. (2008, 2009) to convert backscatter coefficient changes to surface snow density variations: for a smooth surface, a surface snow density increase of 100 kg m−3 results in a backscatter coefficient increase of 0.3 dB at Ku band. It results in an estimation of the surface snow density decrease from ENVISAT–RA-2 observations of around −30 kg m−3 yr−1, which is about 2.3 times larger in amplitude than the trend found from AMSR-E observations.
5.5 Uncertainties and discussion
We first present an assessment of the uncertainties and then discuss the importance of several caveats that may affect the accuracy of ρsat: the effects of using a constant vertical profile of temperature, of variations of the azimuthal viewing angle, and of considering the temporal evolution of the surface roughness and the snow deeper into the snowpack.
5.5.1 Uncertainty assessment
We use here the signal-to-noise ratio (SNR) to characterize the significance of our results. SNR is the ratio between the mean of the observed data over the standard deviation of the background noise. In our time series of surface snow density, we assume that the standard deviation of quick variations to be noise even though part of it may be a natural signal. That gives an upper limit of the noise. We found a SNR of 5.9. This value is high enough to conclude that a real signal emerges from the noise, and thus the negative trend of surface snow density is significant at Dome C. Furthermore, the spatial variability of surface snow density (41.6 kg m−3) was measured near Concordia Station, which is smaller than the standard deviation of the retrieved density (63.5 kg m−3). That indicates that variations in the retrieved density are not only due to the spatial variability. However, the spatial variability is not directly taken into account in the retrieved density. This results in uncertainties in the retrieved density (Brucker et al., 2011; Picard et al., 2014). In the last study, the authors found an alternation every 15–25 m of dense and hard snow and light and loose snow areas. They found smaller density variations at larger scales which indicate that the spatial variability of density exists at smaller scales than the AMSR-E satellite pixel (625 km2). They conclude that changes in emissivity, as observed by Lacroix et al. (2009), might be solely due to changes in the proportion of dense and hard snow features without significant changes in surface properties. In this study, we conclude that the decrease in surface snow density can not be solely due to a decrease in the proportion of dense and hard snow features because the trend is observed in other datasets which have very different spatial scales, from a scale of a few metres for in situ measurements up to hectometre or kilometre scales for active microwave observations.
5.5.2 Caveats affecting the accuracy of the retrieved density
The vertical profile of temperature
Figure 9 shows the time series of ρsat using either the vertical temperature profile of the day or a temperature profile that is constant over time as used in Sect. 5.3 to retrieve the surface snow density. Both curves overlap each other very well which confirms the small influence of the temperature profile on ρsat. This is not surprising, since we already showed the limited influence of temperature changes of the upper layer (Fig. 4). When considering a constant profile of temperature, the standard deviation of the retrieved density is 59.5 kg m−3, slightly higher than when the actual temperature profile of each day is used (57.4 kg m−3). The overall trend of the retrieved snow density is −11.2 and −10.2 kg m−3 yr−1, respectively, when using the vertical temperature profile of each day or a constant profile of temperature.
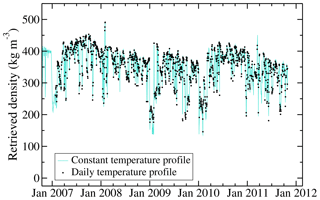
Figure 9Time series of the snow density near the surface ρsat at Dome C, Antarctica, retrieved from AMSR-E passive microwave observations and covering the period from 1 December 2006 to 4 October 2011: (black dots) using the temperature profile of each day and (solid grey line) using a temperature profile that is constant over time.
The azimuthal viewing angle
If satellite observations were performed over an isotropic surface, the azimuth angle would have no effect on the measurements. This is not the case over the Antarctic Plateau, as many studies demonstrated the effect of azimuthal variation on satellite measurements (Fung and Chen, 1981; Tsang, 1991; Shuman et al., 1993; Li et al., 2008; Narvekar et al., 2010). However, this effect is weak in our study because we use daily averaged observations and the first two components of the Stokes vector that minimize the effect of variations in the azimuthal viewing angle (Long et al., 2001; Li et al., 2008; Narvekar et al., 2010). Furthermore, passive microwaves are less sensitive than active microwaves to the azimuth viewing angle of the observations (Ulaby et al., 1981). Lastly, the surface is flat around Dome C, lower than 1 m km−1 (Rémy et al., 1999), and thus the effect of azimuthal variations in the surface roughness on brightness temperature remains limited (Rémy and Parouty, 2009; Narvekar et al., 2010).
The surface roughness
The roughness of the snow surface has a direct influence on passive and active microwave observations (Rémy and Minster, 1991; Shuman et al., 1993; Flament and Rémy, 2012; Rémy et al., 2014; Adodo et al., 2018). Surface roughness ranges from ice sheet topography (100 km wavelength) and large dune fields (1 to 10 km wavelength) to small features on the surface, from millimetre to metre scales (hoar crystals and sastrugi, Shuman et al., 1993; Long and Drinkwater, 2000; Libois et al., 2014). Our method requires the surface roughness to have a negligible effect, and thus we discuss this assumption first for active observations and then for passive observations.
The radar backscatter is often reduced by an increase in the surface roughness. The slopes of the large-scale topography around Dome C are small enough, less than 1 m km −1, to only have a minor impact of the radar backscatter (Flament and Rémy, 2012). The pluri-annual trend can, however, be reduced considering a rough surface (Lacroix et al., 2008; Adodo et al., 2018). Nevertheless, even with a lesser negative trend, ENVISAT and QuikSCAT observations confirm the decrease in the surface snow density observed at Dome C by AMSR-E with completely independent data. QuikSCAT observations also suggest a slow evolution of the surface roughness.
Concerning passive microwave observations, as discussed in Champollion et al. (2013), the surface roughness influence is higher at vertical polarization than at horizontal polarization. The surface roughness tends to increase the polarization ratio and reduce the retrieved density. As a result, the trend of the retrieved surface snow density can be reduced by an increase in the surface roughness with time. The following reasons argue in favour of a small effect of the surface roughness even though we can not conclude this definitively: (1) Long and Drinkwater (2000) found a relatively low sensitivity of the polarization ratio to surface roughness; (2) the surface roughness is mainly governed by wind and, during the last decade, no clear wind evolution was found; and (3) most of the time, the lower the frequency, the higher the sensitivity of active microwave observations to surface roughness. This relationship is unclear for AMSR-E observations due to the difference of zenith viewing angle (Tsang, 1991; Liang et al., 2009). However, we should observe a frequency dependence of the polarization ratio evolution if the surface roughness has evolved with time, at least for small-scale roughness. Yet, the PR trends from AMSR-E are 0.00319 and 0.00326 at, respectively, 37 and 19 GHz, which is thus compatible with a limited evolution of the small-scale roughness. Concerning the large-scale topography around Dome C, the minor impact on satellite observations has been previously discussed.
The snow at depth
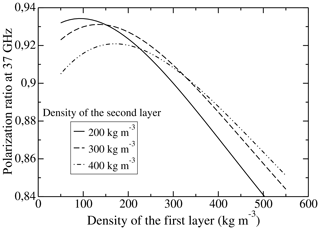
The snow below the top layer up to few metres depth influences the polarization ratio through internal reflections. Changes in volume scattering (due to snow grains), caused by the evolution of snow deeper into the snowpack, certainly have a negligible direct effect on the retrieved density. However, snow evolution can change the penetration depth of the microwave emissions and consequently change the number of snow–snow interfaces caused by abrupt changes in the snow density profile. Interface reflections are nearly independent of the wavelength according to Fresnel coefficients. The influence on ρsat of snow changes deeper into the snowpack should thus be independent of the frequency. We consider an extreme case where the density stratification is always increasing with the decrease in surface snow density, keeping other snow parameters constant. The amount of internal reflections influences the PR more than the amplitude of the density difference between two layers. In addition, surface reflection is at least 4–5 times higher than internal reflections (Fig. 10). The case considered here (increase in density stratification) leads to a decrease in the PR with time and thus an increase in the retrieved surface snow density. As a result, the trend of the retrieved density can be reduced by an increase in the snow density stratification. However, this effect probably remains small because changing the density of the second layer from 200 to 400 kg m−3 involves changes in the relationship between ρsat and PR37 lower than 20 % (Fig. 10). Furthermore, changing the snow density of the third layer results in an influence on the PR slope of less than 10 %. As a result, decreasing the snow density of the second layer by 10 kg m−3 (which is the trend of the retrieved density) has a weak influence on PR at 37 GHz. Finally, modelling the evolution of the density profile is needed to definitively quantify its effect on the retrieved surface snow density. However, the sign of the trend will remain negative and the order of magnitude will probably remain the same.
The snow density near the surface at Dome C on the East Antarctic Plateau has been estimated from passive microwave observations over nearly 10 years. The surface snow density retrieval method is based on the difference of Fresnel reflection coefficients between horizontally and vertically polarized brightness temperatures at the air–snow interface. The brightness temperatures were acquired by AMSR-E from 2002 to 2011. The DMRT-ML model has been used to compute the polarization ratio (the ratio of horizontal on vertical brightness temperature) at the TOA using in situ profiles of snow parameters following Brucker et al. (2011). The comparison between modelled and observed brightness temperatures at 19 and 37 GHz, as well as the polarization ratio sensitivity analyses to parameters of the top snow layer (3 cm thick), has highlighted a relationship between the variations in the polarization ratio at 37 GHz and the variations in the snow density very close to the surface (approximately the top 3 cm of snow).
The main result of this study is the significant negative pluri-annual trend of surface snow density of about −13 kg m−3 yr−1. We have not found a similar trend in the climatic conditions to explain such trend, even though it is likely that the cause is a change of atmospheric origin. This result has important consequences for surface mass balance estimation or regional climate modelling. Snow precipitation over the East Antarctic Plateau is expected to increase during the coming century (Krinner et al., 2007). The time series also show an annual cycle as well as daily to weekly large density variations. The annual cycle could be linked to the amount of precipitation and the growing rate of surface snow crystal size during the summer (Picard et al., 2012). The quick variations are certainly the result of interactions between the wind and the surface snow as well as the formation and disappearance of hoar crystals (Champollion et al., 2013; Libois et al., 2014).
The retrieved time series of surface snow density has been compared to data available in the literature and to in situ measurements. All data agreed on the range of surface density values. Hoar crystals have a density between 125 and 178 kg m−3 and, when absent, surface snow density varies between 150 and 520 kg m−3 according to in situ measurements and between 136 and 508 kg m−3 for satellite-retrieved density. In situ measurements show the same negative trend as the satellite observations of about 10 kg m−3 yr−1. The pluri-annual decrease in surface snow density is also visible in active microwave observations (radar backscatter coefficient extracted from ENVISAT–RA-2 and radar polarization ratio calculated from SeaWinds–QuikSCAT). As a result, SeaWinds–QuikSCAT observations also show a probable absence of evolution of the surface roughness. An overestimation of the decrease in surface snow density can, however, not be totally excluded, especially if surface roughness and/or density stratification in the snowpack increase in parallel with time.
Thanks to the passive microwave observations that are all-weather, daily, and available for more than 30 years, this method can potentially be applied to the whole Antarctic Ice Sheet, after addressing the following issues: (1) the inclusion of surface roughness, which can be more significant in other regions than at Dome C (Adodo et al., 2018), and the snow at depth in the retrieval method; (2) the inclusion of the regions where melt occurs (Picard et al., 2007); and (3) the inter-calibration of the different passive microwave satellites.
References describing the individual satellite datasets are provided in the method section. DMRT-ML model code is available at http://pp.ige-grenoble.fr/pageperso/picardgh/dmrtml/ (last access: 8 April 2019). The snow property profiles, the surface snow density observations, and the retrieved surface snow density are publicly available online through Zenodo at https://doi.org/10.5281/zenodo.2590150 (Champollion, 2019).
GP, MF, LA, and NC conceived the study. NC performed the simulation, collected and interpreted QuikSCAT data, carried out the data analysis, interpreted the results, and wrote the manuscript with the important help of GP. GP collected AMSR-E data and is the main developer of the DMRT-ML model. LA and EL measured the snow temperature profiles. LA performed the measurements devoted to the study of the surface snow density variability. NC, GP, LA, GM, and EL participated to the collection of all other in situ measurements. FR collected and interpreted ENVISAT data. All the co-authors discussed the results and participated in the writing of the manuscript.
The authors declare that they have no conflict of interest.
AMSR-E, RA-2 and QuikSCAT data were, respectively, obtained from the National
Snow and Ice Data Center (NSIDC) at the University of Colorado, the Centre
for Topographic studies of the Ocean and Hydrosphere (CTOH) supported by the
European Space Agency (ESA) ENVISAT–RA-2 programme, and from the NASA-sponsored scatterometer climate
record pathfinder (SCP) at Brigham Young University. We are very grateful to
Ilhan Bourgeois, Sylvain Lafont, and Sébastien Aubin for making snow density
measurements at Dome C during the polar winter. Field measurements around
Concordia Station were made possible by the joint French–Italian Concordia
Program, which established and currently runs the permanent Concordia station
at Dome C. We warmly thank the French polar institute (Institut Paul
Emile Victor, IPEV) and the Italian polar programme (Programma Nazionale di
Ricerca in Antartide, PNRA). Finally, this work was supported by the
Programme National de Télédétection Spatiale (PNTS), the IPEV programmes
(IPEV–CALVA and IPEV–GLACIOLOGIE) and the project MAPME (Monitoring of
Antarctic Plateau by means of Multi-Frequency Microwave Emission) funded by
PNRA. We are grateful to the two reviewers and the editor, whose comments and
discussion improved and clarified the manuscript.
The article processing charges for this open-access
publication were covered by the University of Bremen.
This paper was edited by Martin Schneebeli and reviewed by Zoe Courville and one anonymous referee.
Abdalati, W. and Steffen, K.: Accumulation and hoar effects on microwave emission on the Greenland ice sheet dry snow zones, J. Glaciol., 44, 523–531, 1998. a
Adodo, F. I., Remy, F., and Picard, G.: Seasonal variations of the backscattering coefficient measured by radar altimeters over the Antarctic Ice Sheet, The Cryosphere, 12, 1767–1778, https://doi.org/10.5194/tc-12-1767-2018, 2018. a, b, c, d, e, f
Alley, R. B., Bolzan, J. F., and Whillans, I. M.: Polar firn densification and grain growth, Ann. Glaciol., 3, 7–11, 1982. a
Arnaud, L., Picard, G., Champollion, N., Domine, F., Gallet, J.-C., Lefebvre, E., Fily, M., and Barnola, J.-M.: Instruments and Methods. Measurement of vertical profiles of snow specific surface area with a 1 cm resolution using infrared reflectance: instrument description and validation, J. Glaciol., 57, 17–29, https://doi.org/10.3189/002214311795306664, 2011. a, b, c, d
Arthern, R. J., Winnebrenner, D. P., and Vaughan, D. G.: Antarctic snow accumulation mapped using polarization of 4.3-cm wavelength microwave emission, J. Geophys. Res., 111, 2156–2202, https://doi.org/10.1029/2004JD005667,2006. a, b, c
Arthern, R. J., Vaughan, D. G., Rankin, A. M., Mulvaney, R., and Thomas, E. R.: In situ measurements of Antarctic snow compaction compared with predictions of models, J. Geophys. Res., 115, F03011, https://doi.org/10.1029/2009JF001306, 2010. a
Born, M. and Wolf, E.: Principles of Optics Electromagnetic. Theory of Propagation, Interference and Diffraction of Light, Cambridge University Press, https://doi.org/10.1017/CBO9781139644181, 1999. a
Brucker, L., Picard, G., Arnaud, L., Barnola, J.-M., Schneebeli, M., Brunjail, H., Lefebvre, E., and Fily, M.: Modeling time series of microwave brightness temperature at Dome C, Antarctica, using vertically resolved snow temperature and microstructure measurements, J. Glaciol., 57, 171–182, https://doi.org/10.3189/002214311795306736, 2011. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q
Brucker, L., Dinnat, E., Picard, G., and Champollion, N.: Effect of Snow Surface Metamorphism on Aquarius L-Band Radiometer Observations at Dome C, Antarctica, IEEE T. Geosci. Remote, 52, 7408–7417, https://doi.org/10.1109/TGRS.2014.2312102, 2014. a, b, c
Brun, E., Six, D., Picard, G., Vionnet, V., Arnaud, L., Bazile, E., Boone, A., Bouchard, A., Genthon, C., Guidard, V., Le Moigne, P., Rabier, F., and Seity, Y.: Snow/atmosphere coupled simulation at Dome C, Antarctica, J. Glaciol., 57, 721–736, https://doi.org/doi:10.3189/002214311797409794, 2011. a, b, c
Cavalieri, D., Markus, T., and Comiso, J.: AMSR-E/Aqua Daily L3 25 km Brightness Temperature & Sea Ice Concentration Polar Grids. Version 3, NASA National Snow and Ice Data Center Distributed Active Archive Center, https://doi.org/10.5067/AMSR-E/AE_SI25.003, 2014. a
Champollion, N.: Évolution de la surface de neige sur le plateau Antarctique: observation in situ et satellite, PhD thesis, Université de Grenoble Alpes, Grenoble, 2013. a, b
Champollion, N.: Snow properties measurements (in situ & retrived from satellite) at Dome C, East Antarctica Plateau [Data set], The Cryosphere, Zenodo, https://doi.org/10.5281/zenodo.2590150, 2019. a
Champollion, N., Picard, G., Arnaud, L., Lefebvre, E., and Fily, M.: Hoar crystal development and disappearance at Dome C, Antarctica: observation by near-infrared photography and passive microwave satellite, The Cryosphere, 7, 1247–1262, https://doi.org/10.5194/tc-7-1247-2013, 2013. a, b, c, d, e, f, g, h, i, j, k, l
Conger, S. M. and McClung, D. M.: Comparison of density cutters for snow profile observations, J. Glaciol., 55, 163–169, https://doi.org/10.3189/002214309788609038, 2009. a, b, c
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J., Park, B., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
Domine, F., Salvatori, R., Legagneux, L., Salzano, R., Fily, M., and Casacchia, R.: Correlation between the specific surface area and the short wave infrared (SWIR) reflectance of snow, Cold Reg. Sci. Technol., 46, 60–68, https://doi.org/10.1016/j.coldregions.2006.06.002, 2006. a, b, c
Domine, F., Albert, M., Huthwelker, T., Jacobi, H.-W., Kokhanovsky, A. A., Lehning, M., Picard, G., and Simpson, W. R.: Snow physics as relevant to snow photochemistry, Atmos. Chem. Phys., 8, 171–208, https://doi.org/10.5194/acp-8-171-2008, 2008. a, b
Dupont, F., Picard, G., Royer, A., Fily, M., Roy, A., Langlois, A., and Champollion, N.: Modeling the microwave emission of bubbly ice: Applications to blue ice and superimposed ice in the Antarctic and Arctic, IEEE T. Geosci. Remote, 52, 6639–6651, https://doi.org/10.1109/TGRS.2014.2299829, 2013. a, b, c
Early, D. and Long, D.: Image Reconstruction and Enhanced Resolution Imaging from Irregular Samples, IEEE T. Geosci. Remote, 39, 291–302, https://doi.org/10.1109/36.905237, 2001. a, b
Eisen, O., Frezzotti, M., Genthon, C., Isaksson, E., Magand, O., Van den Broeke, M. R., Dixon, D. A., Ekaykin, A., Holmlund, P., Kameda, T., Karlöf, L., Kaspari, S., Lipenkov, V., Oerter, H., Takahashi, S., and Vaughan, D. G.: Ground-based measurements of spatial and temporal variability of snow accumulation in East Antarctica, Rev. Geophys., 46, 1–39, https://doi.org/10.1029/2006RG000218, 2008. a, b, c
Favier, V., Agosta, C., Genthon, C., Arnaud, L., Trouvillez, A., and Gallée, H.: Modeling the mass and surface heat budgets in a coastal blue ice area of Adelie Land, Antarctica, J. Geophys. Res., 116, F03017, https://doi.org/10.1029/2010JF001939, 2011. a
Favier, V., Agosta, C., Parouty, S., Durand, G., Delaygue, G., Gallée, H., Drouet, A.-S., Trouvilliez, A., and Krinner, G.: An updated and quality controlled surface mass balance dataset for Antarctica, The Cryosphere, 7, 583–597, https://doi.org/10.5194/tc-7-583-2013, 2013. a
Fettweis, X., Franco, B., Tedesco, M., van Angelen, J. H., Lenaerts, J. T. M., van den Broeke, M. R., and Gallée, H.: Estimating the Greenland ice sheet surface mass balance contribution to future sea level rise using the regional atmospheric climate model MAR, The Cryosphere, 7, 469–489, https://doi.org/10.5194/tc-7-469-2013, 2013. a, b
Flament, T. and Rémy, F.: Dynamic thinning of Antarctic glaciers from along-track repeat radar altimetry, J. Glaciol., 58, 830–840, https://doi.org/10.3189/2012JoG11J118, 2012. a, b, c
France, J. L., King, M. D., Frey, M. M., Erbland, J., Picard, G., Preunkert, S., MacArthur, A., and Savarino, J.: Snow optical properties at Dome C (Concordia), Antarctica; implications for snow emissions and snow chemistry of reactive nitrogen, Atmos. Chem. Phys., 11, 9787–9801, https://doi.org/10.5194/acp-11-9787-2011, 2011. a
Fréville, H., Brun, E., Picard, G., Tatarinova, N., Arnaud, L., Lanconelli, C., Reijmer, C., and van den Broeke, M.: Using MODIS land surface temperatures and the Crocus snow model to understand the warm bias of ERA-Interim reanalyses at the surface in Antarctica, The Cryosphere, 8, 1361–1373, https://doi.org/10.5194/tc-8-1361-2014, 2014. a, b
Frezzotti, M., Pourchet, M., Flora, O., Gandolfi, S., Gay, M., Urbini, S., Vincent, C., Becagli, S., Gragnani, R., Proposito, M., Severi, M., Traversi, R., Udisti, R., and Fily, M.: Spatial and temporal variability of snow accumulation in East Antarctica from traverse data, J. Glaciol., 51, 113–124, https://doi.org/10.3189/172756505781829502, 2005. a, b
Frezzotti, M., Scarchilli, C., Becagli, S., Proposito, M., and Urbini, S.: A synthesis of the Antarctic surface mass balance during the last 800 yr, The Cryosphere, 7, 303–319, https://doi.org/10.5194/tc-7-303-2013, 2013. a
Fujita, S., Holmlund, P., Andersson, I., Brown, I., Enomoto, H., Fujii, Y., Fujita, K., Fukui, K., Furukawa, T., Hansson, M., Hara, K., Hoshina, Y., Igarashi, M., Iizuka, Y., Imura, S., Ingvander, S., Karlin, T., Motoyama, H., Nakazawa, F., Oerter, H., Sjöberg, L. E., Sugiyama, S., Surdyk, S., Ström, J., Uemura, R., and Wilhelms, F.: Spatial and temporal variability of snow accumulation rate on the East Antarctic ice divide between Dome Fuji and EPICA DML, The Cryosphere, 5, 1057–1081, https://doi.org/10.5194/tc-5-1057-2011, 2011. a
Fung, A. and Chen, M.: Emission from an innhomogeneous layer with irregular interfaces, Radio Sci., 16, 289–298, https://doi.org/10.1029/RS016i003p00289, 1981. a
Gallet, J.-C., Domine, F., Arnaud, L., Picard, G., and Savarino, J.: Vertical profile of the specific surface area and density of the snow at Dome C and on a transect to Dumont D'Urville, Antarctica – albedo calculations and comparison to remote sensing products, The Cryosphere, 5, 631–649, https://doi.org/10.5194/tc-5-631-2011, 2011. a, b, c
Gallet, J.-C., Domine, F., Savarino, J., Dumont, M., and Brun, E.: The growth of sublimation crystals and surface hoar on the Antarctic plateau, The Cryosphere, 8, 1205–1215, https://doi.org/10.5194/tc-8-1205-2014, 2014. a, b, c, d
Genthon, C., Town, M. S., Six, D., Favier, V., Argentini, S., and Pellegrini, A.: Meteorological atmospheric boundary layer measurements and ECMWF analyses during summer at Dome C, Antarctica, J. Geophys. Res., 115, D05104, https://doi.org/10.1029/2009JD012741, 2010. a
Gergely, M., Schneebeli, M., and Roth, K.: First experiments to determine snow density from diffuse near-infrared transmittance, Cold Reg. Sci. Technol., 64, 81–86, https://doi.org/10.1016/j.coldregions.2010.06.005, 2010. a
Groh, A., Ewert, H., Rosenau, R., Fagiolini, E., Gruber, C., Floricioiu, D., Abdel Jaber, W., Linow, S., Flechtner, F., Eineder, M., Dierking, W., and Dietrich, R.: Mass, Volume and Velocity of the Antarctic Ice Sheet: Present-Day Changes and Error Effects, Surv. Geophys., 35, 1481–1505, https://doi.org/10.1007/s10712-014-9286-y, 2014. a
Groot Zwaaftink, C. D., Cagnati, A., Crepaz, A., Fierz, C., Macelloni, G., Valt, M., and Lehning, M.: Event-driven deposition of snow on the Antarctic Plateau: analyzing field measurements with SNOWPACK, The Cryosphere, 7, 333–347, https://doi.org/10.5194/tc-7-333-2013, 2013. a, b, c, d
Jin, Y.-Q.: Electromagnetic scattering modelling for quantitative remote sensing, World Scientific, 348 pp., https://doi.org/10.1142/2253, 1994. a
Krinner, G., Magand, O., Simmonds, I., Genthon, C., and Dufresne, J.-L.: Simulated Antarctic precipitation and surface mass balance at the end of the twentieth and twenty-first centuries, Clim. Dynam., 28, 215–230, https://doi.org/10.1007/s00382-006-0177-x, 2007. a
Lacroix, P., Dechambre, M., Legrésy, B., Blarel, F., and Rémy, F.: On the use of the dual-frequency ENVISAT altimeter to determine snowpacks properties of the Antarctic ice sheet, Remote Sens. Environ., 112, 1712–1729, https://doi.org/10.1016/j.rse.2007.08.022, 2008. a, b, c, d
Lacroix, P., Legrésy, B., Rémy, F., Blarel, F., Picard, G., and Brucker, L.: Rapid change of snow surface properties at Vostok, East Antarctica, revealed by altimetry and radiometry, Remote Sens. Environ., 113, 2633–2641, https://doi.org/doi:10.1016/j.rse.2009.07.019, 2009. a, b, c, d
Leduc-Leballeur, M., Picard, G., Mialon, A., Arnaud, L., Lefebre, F., Possenti, P., and Kerr, Y.: Modeling L-Band Brightness Temperature at Dome C in Antarctica and Comparison With SMOS Observations, IEEE T. Geosci. Remote, 53, 4022–4032, https://doi.org/10.1109/TGRS.2015.2388790, 2015. a, b, c
Leduc-Leballeur, M., Picard, G., Macelloni, G., Arnaud, L., Brogioni, M., Mialon, A., and Kerr, Y.: Influence of snow surface properties on L-band Brightness temperature at Dome C, Antarctica, Remote Sens. Environ., 199, 427–436, https://doi.org/10.1016/j.rse.2017.07.035, 2017. a, b, c, d, e, f, g
Legrésy, B., Papa, F., Rémy, F., Vinay, G., van den Bosch, M., and Zanife, O.-Z.: ENVISAT radar altimeter measurements over continental surfaces and ice caps using the ICE-2 retracking algorithm, Remote Sens. Environ., 95, 150–163, https://doi.org/10.1016/j.rse.2004.11.018, 2005. a
Lenaerts, J. T. M. and van den Broeke, M. R.: Modeling drifting snow in Antarctica with a regional climate model: 2. Results, J. Geophys. Res., 117, D05109, https://doi.org/10.1029/2010JD015419, 2012. a
Li, L., Gaiser, P., Albert, M. R., Long, D. G., and Twarog, E. M.: WindSat Passive Microwave Polarimetric Signatures of the Greenland Ice Sheet, IEEE T. Geosci. Remote, 46, 2622–2631, https://doi.org/10.1109/TGRS.2008.917727, 2008. a, b
Liang, D., Tse, K., Tan, Y., Tsang, L., and Kung Hau, D.: Scattering and Emission in Snow Based on QCA/DMRT and Numerical Maxwell Model of 3Dimentional Simulations (NMM3D), MicroRad, IEEE Geoscience and Remote Sensing Society, 197–202, https://doi.org/10.1109/MICRAD.2006.1677088, 2006. a
Liang, D., Xu, X., Tsang, L., Andreadis, K. M., and Josberger, E. G.: The Effects of Layers in Dry Snow on Its Passive Microwave Emissions Using Dense Media Radiative Transfer Theory Based on the Quasicrystalline Approximation (QCA/DMRT), IEEE T. Geosci. Remote, 46, 3663–3671, https://doi.org/10.1109/TGRS.2008.922143, 2008. a
Liang, D., Xu, P., Tsang, L., Gui, Z., and Chen, K.: Electromagnetic scattering by rough surfaces with larges heights and slopes with applications to microwave remote sensing of rough surface over layered media, Prog. Electromagn. Res., 95, 199–218, https://doi.org/10.2528/PIER09071413, 2009. a, b
Libois, Q., Picard, G., France, J. L., Arnaud, L., Dumont, M., Carmagnola, C. M., and King, M. D.: Influence of grain shape on light penetration in snow, The Cryosphere, 7, 1803–1818, https://doi.org/10.5194/tc-7-1803-2013, 2013. a
Libois, Q., Picard, G., Arnaud, L., Morin, S., and Brun, E.: Modeling the impact of snow drift on the decameter-scale variability of snow properties on the Antarctic Plateau, J. Geophys. Res., 119, 11662–11681, https://doi.org/10.1002/2014JD022361, 2014. a, b, c, d, e, f, g, h
Libois, Q., Picard, G., Arnaud, L., Dumont, M., Lafaysse, M., Morin, S., and Lefebvre, E.: Summertime evolution of snow specific surface area close to the surface on the Antarctic Plateau, The Cryosphere, 9, 2383–2398, https://doi.org/10.5194/tc-9-2383-2015, 2015. a
Long, D. and Daum, D.: Spatial Resolution Enhancement of SSM/I Data, IEEE T. Geosci. Remote, 36, 407–417, https://doi.org/0196-2892(98)00550-6, 1998. a
Long, D., Drinkwater, M., Holt, B., Saatchi, S., and Bertola, C.: Global Ice and Land Climate Studies Using Scatterometer Image Data, EOS T. Am. Geophys. Un., 82, 503–518, https://doi.org/10.1029/01EO00303, 2001. a, b
Long, D. G. and Drinkwater, M. R.: Azimuth Variation in Microwave Scatterometer and Radiometer Data Over Antarctica, IEEE T. Geosci. Remote, 38, 1857–1870, https://doi.org/10.1109/36.851769, 2000. a, b, c
Löwe, H. and Picard, G.: Microwave scattering coefficient of snow in MEMLS and DMRT-ML revisited: the relevance of sticky hard spheres and tomography-based estimates of stickiness, The Cryosphere, 9, 2101–2117, https://doi.org/10.5194/tc-9-2101-2015, 2015. a
Macelloni, G., Brogioni, M., Pampaloni, P., and Cagnati, A.: Multifrequency Microwave Emission From the Dome-C Area on the East Antarctic Plateau: Temporal and Spatial Variability, IEEE T. Geosci. Remote, 45, 2029–2039, https://doi.org/10.1109/TGRS.2007.890805, 2007. a, b
Markus, T., Neumann, T. A., Martino, A., Abdalati, W., Brunt, K., Csatho, B., Farrell, S., Fricker, H., Gardner, A., Harding, D., Jasinski, M., Kwok, R., Magruder, L., Lubin, D., Luthcke, S., Morison, J., Nelson, R., Neuenschwander, A., Palm, S., Popescu, S., Shum, C. K., Schutz, B., Smith, B., Yang, Y., and Zwally, J.: The Ice, Cloud and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation, Remote Sens. Environ., 190, 260–273, 2017. a
Matzl, M. and Schneebeli, M.: Measuring specific surface area of snow by near-infrared photography, J. Glaciol., 52, 558–564, https://doi.org/10.3189/172756506781828412, 2006. a
Mätzler, C., Aebischer, H., and Schanda, E.: Microwave dielectric properties of surface snow, IEEE J. Oceanic Eng., 9, 366–371, https://doi.org/10.1109/JOE.1984.1145644, 1984. a
McMillan, M., Shepherd, A., Sundal, A., Briggs, K., Muir, A., Ridout, A., Hogg, A., and Wingham, D.: Increased ice losses from Antarctica detected by CryoSat-2, Geophys. Res. Lett., 41, 3899–3905, https://doi.org/10.1002/2014GL060111, 2014. a
Mittal, S. K., Singh, M., and Garg, P. K.: Development of an instrument to measure density and moisture content of snow, J. Sci. Ind. Res. Ind., 68, 188–191, 2009. a
Narvekar, P. S., Heygster, G., Jackson, T. J., Bindlish, R., Macelloni, G., and Justus, N.: Passive Polarimetric Microwave Signatures Observed Over Antarctica, IEEE T. Geosci. Remote, 48, 1059–1075, https://doi.org/10.1109/TGRS.2009.2032295, 2010. a, b, c
Palerme, C., Kay, J. E., Genthon, C., L'Ecuyer, T., Wood, N. B., and Claud, C.: How much snow falls on the Antarctic ice sheet?, The Cryosphere, 8, 1577–1587, https://doi.org/10.5194/tc-8-1577-2014, 2014. a
Picard, G., Fily, M., and Gallée, H.: Surface melting derived from microwave radiometers: a climatic indicator of Antarctica, Ann. Glaciol., 46, 29–34, https://doi.org/10.3189/172756407782871684, 2007. a
Picard, G., Brucker, L., Fily, M., Gallée, H., and Krinner, G.: Modeling time series of microwave brightness temperature in Antarctica, J. Glaciol., 55, 537–551, https://doi.org/10.3189/002214309788816678, 2009. a, b, c
Picard, G., Domine, F., Krinner, G., Arnaud, L., and Lefebvre, E.: Inhibition of the positive snow-albedo feedback by precipitation in interior Antarctica, Nat. Clim. Change, 2, 795–798, https://doi.org/10.1038/nclimate1590, 2012. a, b, c
Picard, G., Brucker, L., Roy, A., Dupont, F., Fily, M., Royer, A., and Harlow, C.: Simulation of the microwave emission of multi-layered snowpacks using the Dense Media Radiative transfer theory: the DMRT-ML model, Geosci. Model Dev., 6, 1061–1078, https://doi.org/10.5194/gmd-6-1061-2013, 2013. a, b, c, d, e
Picard, G., Royer, A., Arnaud, L., and Fily, M.: Influence of meter-scale wind-formed features on the variability of the microwave brightness temperature around Dome C in Antarctica, The Cryosphere, 8, 1105–1119, https://doi.org/10.5194/tc-8-1105-2014, 2014. a, b, c, d, e, f, g, h
Proksch, M., Rutter, N., Fierz, C., and Schneebeli, M.: Intercomparison of snow density measurements: bias, precision, and vertical resolution, The Cryosphere, 10, 371–384, https://doi.org/10.5194/tc-10-371-2016, 2016. a
Rémy, F. and Minster, J.: A comparison between active and passive microwave measurements of the Antarctic ice sheet and their association with the surface katabatic winds, J. Glaciol., 37, 3–10, 1991. a
Rémy, F. and Parouty, S.: Antarctic Ice Sheet and Radar Altimetry: A Review, Radio Sci., 1, 1212–1239, https://doi.org/10.3390/rs1041212, 2009. a, b, c
Rémy, F., Shaeffer, P., and Legrésy, B.: Ice flow physical processes derived from the ERS-1 high-resolution map of the Antarctica and Greenland ice sheets, Geophys. J. Int., 139, 645–656, https://doi.org/10.1046/j.1365-246x.1999.00964.x, 1999. a
Rémy, F., Flament, T., Michel, A., and Verron, J.: Ice sheet survey over Antarctica with satellite altimetry: ERS-2, EnviSat, SARAL/AltiKa, the key importance of continuous observations along the same repeat orbit, Int. J. Remote Sens., 35, 5497–5512, https://doi.org/10.1080/01431161.2014.926419, 2014. a, b, c
Rosenkranz, P.: Rough-sea microwave emissivities measured with the SSM/I, IEEE T. Geosci. Remote, 30, 1081–1085, https://doi.org/10.1109/36.175345, 1992. a, b
Roy, A., Picard, G., Royer, A., Montpetit, B., Dupont, F., Langlois, A., Derksen, C., and Champollion, N.: Brightness temperature simulations of the Canadian seasonal snowpack driven by measurements of snow specific surface area, IEEE T. Geosci. Remote, 51, 4692–4704, https://doi.org/10.1109/TGRS.2012.2235842, 2012. a, b, c, d
Schwank, M. and Naderpour, R.: Snow Density and Ground Permittivity Retrieved from L-Band Radiometry: Melting Effects, Radio Sci., 10, 354, https://doi.org/10.3390/rs10020354, 2018. a
Shuman, C. A. and Alley, R. B.: Spatial and temporal characterization of hoar formation in central Greenland using SSM/I brightness temperatures, Geophys. Res. Lett., 20, 2643–2646, https://doi.org/10.1029/93GL02810, 1993. a
Shuman, C. A., Alley, R. B., and Anandakrishnan, S.: Characterization of a hoar-development episode using SSM/I brightness temperatures in the vicinity of GISP2 site, Greenland, Ann. Glaciol., 17, 183–188, https://doi.org/01/1993;17:183-188, 1993. a, b, c, d, e, f
Sommer, C. G., Wever, N., Fierz, C., and Lehning, M.: Investigation of a wind-packing event in Queen Maud Land, Antarctica, The Cryosphere, 12, 2923–2939, https://doi.org/10.5194/tc-12-2923-2018, 2018. a
Spencer, M., Wu, C., and Long, D.: Improved Resolution Backscatter Measurement with the SeaWinds Pencil-Beam Scatterometer, IEEE T. Geosci. Remote, 38, 89–104, https://doi.org/0196-2892(00)00017-6, 2000. a
Surdyk, S.: Using microwave brightness temperature to detect short-term surface air temperature changes in Antarctica: An analytical approach, Remote Sens. Environ., 80, 256–271, https://doi.org/10.1016/S0034-4257(01)00308-X, 2002a. a
Surdyk, S.: Low microwave brightness temperatures in central Antarctica: observed features and implications, Ann. Glaciol., 34, 134–140, https://doi.org/10.3189/172756402781817464, 2002b. a, b
Tedesco, M.: Remote Sensing of the Cryosphere, Cryosphere Science Series, John Wiley & Sons, Ltd, https://doi.org/10.1002/9781118368909, 2015. a
Tsang, L.: Polarimetic Passive Microwave Remote Sensing of Random Discrete Scatterers and Rough Surfaces, J. Electromagnet. Wave., 5, 41–57, https://doi.org/10.1163/156939391X00464, 1991. a, b
Tsang, L., Chen, C.-T., Chang, A. T., Guo, J., and Ding, K.-H.: Dense media radiative transfer theory based on quasicrystalline approximation with application to passive microwave remote sensing of snow, Radio Sci., 35, 741–749, https://doi.org/10.1029/1999RS002270, 2000a. a
Tsang, L., Kong, J., and Ding, K.: Scattering of Electromagnetic Waves, Theory and Applications, vol. 1, Wiley Interscience, 2000b. a, b
Tsang, L., Xu, P., and Chen, K. S.: Third and fourth stokes parameters in polarimetric passive microwave remote sensing of rough surfaces over layered media, Microw. Opt. Techn. Let., 50, 3063–3069, https://doi.org/10.1002/mop.23892, 2008. a
Ulaby, F. T., Moore, R. K., and Fung, A. K.: Microwave Remote Sensing: Active and Passive, Volume I: Fundamentals and Radiometry, Artech House Publishers, Massachusetts, ISBN ISBN is 978-0890061909, 1981. a, b
Ulaby, F. T., Moore, R. K., and Fung, A. K.: Microwave Remote Sensing: Active and Passive, Volume II: Radar Remote Sensing and Surface Scattering and Emission Theory, Artech House Publishers, Massachusetts, ISBN 978-0890061916, 1982. a, b
Verfaillie, D., Fily, M., Le Meur, E., Magand, O., Jourdain, B., Arnaud, L., and Favier, V.: Snow accumulation variability derived from radar and firn core data along a 600 km transect in Adelie Land, East Antarctic plateau, The Cryosphere, 6, 1345–1358, https://doi.org/10.5194/tc-6-1345-2012, 2012. a, b
Vernon, C. L., Bamber, J. L., Box, J. E., van den Broeke, M. R., Fettweis, X., Hanna, E., and Huybrechts, P.: Surface mass balance model intercomparison for the Greenland ice sheet, The Cryosphere, 7, 599–614, https://doi.org/10.5194/tc-7-599-2013, 2013. a
Walden, V. P., Warren, S. G., and Tuttle, E.: Atmospheric Ice Crystals over the Antarctic Plateau in Winter, J. Appl. Meteorol., 42, 1391–1405, https://doi.org/10.1175/1520-0450(2003)042<1391:AICOTA>2.0.CO;2, 2003. a
Warren, S. G. and Brandt, R. E.: Optical constants of ice from the ultraviolet to the microwave: A revised compilation, J. Geophys. Res., 113, D14220, https://doi.org/10.1029/2007JD009744, 2008. a
Xiie, A., Allison, I., Xiao, C., Wang, S., Ren, J., and Qin, D.: Assessment of air temperatures from different meteorological reanalyses for the East Antarctic region between Zhonshan and Dome A, Sci. China Earth Sci., 57, 1538–1550, 2014. a