the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Impacts of topographic shading on direct solar radiation for valley glaciers in complex topography
Matthew Olson
Summer Rupper
Topographic shading, including both shaded relief and cast shadowing, plays a fundamental role in determining direct solar radiation on glacier ice. However, shading has been oversimplified or incorrectly incorporated in surface energy balance models in some past studies. In addition, no systematic studies have been conducted to evaluate relationships between shading and other topographic characteristics. Here we develop a topographic solar radiation model to examine the variability in irradiance throughout the glacier melt season due to topographic shading and combined slope and aspect. We apply the model to multiple glaciers in high-mountain Asia (HMA) and test the sensitivity of shading to valley aspect and latitude. Our results show that topographic shading significantly alters the potential direct clear-sky solar radiation received at the surface for valley glaciers in HMA, particularly for north- and south-facing glaciers. Additionally, we find that shading can be extremely impactful in the ablation zone. Cast shadowing is the dominant mechanism in determining total shading for valley glaciers in parts of HMA, especially at lower elevations. Although shading can be predictable, it is overall extremely variable between glacial valleys. Our results suggest that topographic shading not only is an important factor contributing to surface energy balance but could also influence glacier response and mass balance estimates throughout HMA.
Valley glaciers are an important resource for many local communities, where summer melt is vital for irrigation and drinking sources (Immerzeel et al., 2010). Additionally, after thermal expansion of oceans, mountain glaciers are expected to be the next-largest contributor to sea-level rise over the next century (Vaughan et al., 2014). Improvement to our understanding of these glacial systems is essential in properly quantifying melt and associated impacts, particularly in remote regions where in situ data are sparse.
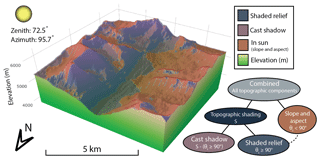
Figure 1Comparing two different shading methods in the Satluj subbasin within the Indus watershed. Shading is calculated for 1 April 2013 at 07:33 GMT+6. Notice the importance of incorporating both methods in order to determine shading in this glacial valley. Both methods, but specifically cast shadows, are most prevalent early in the morning and late in the evenings when the zenith angle is large. Red coloring indicates areas “in sun” that are impacted by a change in irradiance due to the slope and aspect of the surface. Cast shadow, shaded relief, and “slope and aspect” are the three topographic components compared in this paper. Symbols in the flow chart relate to equations in Sect. 2; θi denotes the incidence angle.
During the summer months, net shortwave radiation on a glacier is one of the main components of surface energy balance, often accounting for 75 % or more of available energy at the surface (Gruell and Smeets, 2001; Oerlemans and Klok, 2002). Thus, changes in the amount of solar radiation at the surface will alter the overall global radiation and consequently be a significant influence on surface energy balance. The intensity of solar radiation received at the surface of a glacier is primarily a function of latitude and time of year, with components such as topographic shading, slope, and aspect controlling the distribution of radiation on a local scale.
To facilitate further discussion and analysis, we separate topographic shading into two components: shaded relief and cast shadow. Shaded relief (also referred to as self-shadowing) occurs when a given location is obscured by the sun solely due to the slope and aspect of the terrain. If the angle between the solar position and surface normal at a given location is greater than 90∘, it is treated as “shadow”; if less, it is considered “in sun”, as seen in Fig. 1. This method is also often used as an image enhancing technique for display purposes, also commonly described as a “hillshade” (e.g., ESRI Hillshade Tool).
Cast shadows are the result of shading due to adjacent topography. Nearby features, such as surrounding valley walls, may block the neighboring area from direct solar radiation, as depicted in Fig. 1, particularly in the early and late hours of the day. This effect can be more pronounced near steep terrain and narrow valleys. Because local terrain is unique and solar angles vary constantly, cast shadows must be considered for each sun position over an hourly, daily, and monthly time interval. Additionally, some studies show that direct solar radiation can be obstructed for most of the year on certain steep mountain slopes (Aguilar et al., 2010).
Several glacier-related studies explicitly model topographic shading and allude to the potential importance (e.g., Arnold et al., 2006; Dozier and Frew, 1990; Han et al., 2016; Hock, 1999; Hopkins et al., 2010; Klok and Oerlemans, 2002; Munro and Young, 1982; Williams et al., 1972; and others). Although these studies correctly incorporate topographic shading, most only briefly mention this component. There are, however, a few exceptions that focus some attention on specifying the role of topographic shading. For example, Klok and Oerlemans (2002) show that topographic shading on a glacier in Switzerland can reduce shortwave radiation by more than 10 % at lower elevations, and the combined effect of topography can result in a 37 % overestimation of incoming solar radiation. Munro et al. (1982) also determined that shading is generally greatest at lower elevations in a glacier basin but suggested that the added computational expense may outweigh the overall magnitude of impact on the energy budget for a single Canadian glacier. Alternatively, Arnold et al. (2006) observed a significant effect and general increase in shading with elevation, as well as a large impact near valley walls for an Arctic glacier. Additionally, they suggested that the influence of topography on surface energy balance would be enhanced at higher latitudes. These varying results have created some ambiguity regarding the overall impact of shading on alpine glaciers. In addition, while the above studies demonstrate the influence of shading on solar radiation, these are typically single-glacier case studies, which potentially limits the transferability of the results to other glaciers or broader regions. Further adding to the confusion, numerous other studies claim to incorporate topographic shading in their models but do so incorrectly, leading to erroneous results (Chen et al., 2013; DeBeer and Sharp, 2009; Kumar et al., 1997; Pandey et al., 2016; Plummer and Philips, 2003; Way et al., 2014; Zhang et al., 2015; and others). These studies all overestimate solar radiation by neglecting the influence of cast shadowing, which propagates error throughout calculations of the surface energy balance and glacier melt. In addition, neglecting cast shadowing has led to inaccurate interpretations of the significance of topographic shading and further complicates our understanding of this process. In summary, there has been limited focus on topographic shading on glacier systems, there have been conflicting results from a limited number of case studies, and there are models (still in use) that incorrectly account for shading. Thus, despite recent advances in modeling of incident shortwave radiation, it is still not entirely clear whether topographic shading always has a significant impact on key surface energy terms, or where and when it might be most prevalent. To date, there have been no systematic studies quantifying the magnitude and variability of topographic shading over complex terrain, variable aspect, and differing latitude, which would help address these issues. This study aims to identify the magnitude and spatial patterns of topographic shading on glaciers in complex terrain.
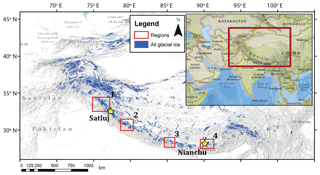
Figure 2High-mountain Asia, showing glacier ice in blue. Two selected glaciers of interest are shown as yellow stars. Four red boxes indicate the areas selected for regional analysis. Regions are centered on the Jammu Kashmir (1), Himachal Pradesh (2), Everest (3), and Bhutan (4) regions. Glacier shapefiles from Arendt et al. (2015), basemap from ESRI (2017).
We select high-mountain Asia (HMA) as our region of interest because of the varied types of complex topography and range of glacier latitudes (Fig. 2). Thus, it is an ideal region in which to assess the role of shading across variable topography, aspect, and latitude. Also, there is little to no previous research regarding the impact of topographic shading on glaciers in this region, so the results will fill in a current knowledge gap. Importantly, improving glacier surface energy and mass balance models is most essential in remote regions where little data exist, such as HMA. However, even where in situ measurements of solar radiation are available, the spatial heterogeneity of energy flux values across the surface of a glacier would require additional topographic information and integrative modeling in order to accurately distribute the point-source solar radiation observations across the glacier. This study focuses on improving the current understanding regarding the impact of both shaded relief and cast shadowing on glaciers in the complex and varied topography of HMA.
In this study, we will use a solar radiation model in conjunction with a topographic model to simulate the distribution of direct solar radiation across glacier surfaces. The models will be used to attribute the change in irradiance due to specific topographic components such as slope and aspect, shaded relief, and cast shadows. Hereafter, “slope and aspect” will refer to a topographic component responsible for changing irradiance values based on the orientation and slope of the surface in unshaded areas of the glacier. In this study, we specifically compare the impact of shaded relief and cast shadows to the collective influence of slope and aspect. We focus on these comparisons in part because slope and aspect are generally assumed to be the dominant topographic factors affecting solar radiation in mountainous terrain (Dozier, 1980). The key inputs to the models will be glacier location and size, and digital elevation models (DEMs).
First, we apply these two models to two individual glaciers in HMA. We then test the sensitivity of each glacier to different valley aspects and latitudes using idealized scenarios. Finally, we evaluate variations in topographic shading across four glacierized basins that represent distinct zones of differing latitude, topography, and climatology within HMA.
2.1 Modeling solar radiation
Accurately determining the position of the sun is essential in order to properly calculate the amount of incoming solar radiation. This is also necessary when considering topographic effects. Assuming a flat plane, the solar position is described by a combination of the zenith (Z) and azimuth angles, which are calculated using standard methods (Iqbal, 1983).
We model potential clear-sky direct solar radiation (Ia), as it passes through the atmosphere, at 15 min time intervals throughout the melt season (1 April–31 September):
where I0 is the solar constant (∼1368 W m−2), R is the sun–earth distance (subscript m refers to mean), ψa is atmosphere clear-sky transmissivity (a constant of 0.75 is used; Hock, 1999), P is atmospheric pressure calculated using a simple lapse rate for dry air, P0 is mean atmospheric pressure at sea level, and Z is local zenith angle (which accounts for the size of air mass that radiation must travel through before arriving at the surface). Equation (1) has been modified from Hock (1999) to exclude the component responsible for attenuation at the surface. This term will be added later in the topographic model.
2.2 Topographic modeling
In alpine terrain, the combination of slope and aspect is generally presumed to be the most influential topographic factor regulating absorbed solar radiation at the surface (Dozier and Frew, 1990). However, some areas surrounded by steep terrain can also be highly influenced by topographic shading (Arnold et al., 2006). Due to the high spatial and temporal variability in the incident angle and topographic shading throughout the day, comparing the impact of these topographic components side by side to assess relative importance can be challenging. Here we present Eqs. (3)–(6) as a means by which to address this issue. We use these equations to calculate the change in irradiance averaged over the course of a day for a given topographic component.
We incorporate two additional terms, incident angle and topographic shading, in conjunction with Eq. (1) to determine the distribution of solar radiation at the surface due to topographic effects. Potential clear-sky solar radiation arriving on an inclined surface is
where Ia is potential atmospheric clear-sky direct solar radiation from Eq. (1); θi is the incident angle; and S is topographic shading, a binary value indicating whether a given cell is in “shade” (0) or “sun” (1). Topographic shading is calculated with a modified ray-tracing algorithm that uses a solar illumination plane perpendicular to the sun's zenith angle in order to determine if a cell is blocked by surrounding cells at a certain zenith and azimuth angle (Corripio, 2003). This method incorporates both self-shading from relief and cast shadows. The incident angle is the zenith angle (Z) modified for a surface with a specific slope and aspect (Iqbal, 1983).
We use variations of Eq. (2) in order to determine the daily mean change in solar radiation from specific topographic components shown in Fig. 1. Equations (3)–(6) show the mean change in solar irradiance due to slope and aspect (incidence angle), shaded relief, cast shadows, and the combined effect of these topographic components:
Figure 3 shows the derivation of these equations with respect to Eq. (2) (model 1) and illustrates the topographic components of interest. In order to determine the influence of each component, a second model is created excluding the component of interest. Equations (3)–(6) calculate the difference between Eq. (2) (model 1) and a model that excludes the topographic component of interest, which is then integrated over the course of a day. The result of these equations is a change in irradiance due to a specific topographic component. Equation (3) shows the daily mean change in solar radiation due to the slope and aspect relative to a flat plane. By incorporating S in this equation, values considered to be in shade are excluded. The mean change in irradiance due to shaded relief is also relative to a flat plane (Eq. 4), as shaded relief also relies on the presence of slope and aspect values. Shaded relief only occurs when the incident angle is greater than or equal to 90∘. Equation (5) shows the mean change in irradiance due to cast shadowing relative to an inclined plane void of cast shadows. This accounts for any change in irradiance due to the slope and aspect, as well as shaded relief. By default, shaded relief is incorporated in both the calculation of the incident angle (θi) and the shading algorithm used to determine topographic shading (S). This allows us to parse out the individual impact from each of these topographic components, for comparison. Finally, Eq. (6) is the combined effect from these three components relative to a flat plane. For each of the equations described above, the mean change in irradiance is equivalent to the integrated difference over the course of a day.
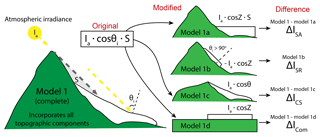
Figure 3Diagram illustrating the derivation of Eqs. (3)–(6). Model 1 (same as Eq. 2) is the base model and incorporates both methods of topographic shading (S) and the effect of slope and aspect (θi). Additional models are also created, each excluding some component of topography. The difference between model 1 and model 1a shows the change in irradiance due to slope and aspect on the surface of the glacier. Model 1b calculates the sum of irradiance that would arrive on a flat surface at locations on the glacier where the incidence angle (θi) is greater than 90∘. Model 1b is the only scenario not dependent on model 1. The difference between model 1 and model 1c shows the change in irradiance due only to cast shadows. Model 1d removes surrounding terrain and assumes the glacier surface is a flat plane, the difference between this and the original model shows the combined effect of removing all topographic information from the DEM.
Our results present a daily mean change in irradiance due to each topographic component, averaged across the entire melt season. For simplicity, we will refer to the daily mean change in irradiance averaged over the melt season as the mean change in irradiance.
2.3 Data
This study utilizes the 30 m resolution Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) global digital elevation model (GDEM) to simulate topographic terrain in the models. Although a 30 m resolution DEM does not fully capture the actual topographic complexity in a glacial valley, it serves as an adequate representation in order to measure the overall effect of surrounding topography on solar radiation within our theoretical framework. DEM resolution is further considered in the discussion in Sect. 4.1 section of this paper.
Glacier boundaries are determined with the latest shapefiles available from the Randolph Glacier Inventory 5.0 and ICIMOD (Arendt et al., 2015; Bajracharya and Shrestha, 2011). Both inventories delineate glacier ice using a variety of techniques to determine glacier boundaries. A buffer of 5 km is generated around the glacier shapefiles in order to include all surrounding topography. Because valley glaciers are constrained by the immediate surrounding topography, only nearby features are able to affect incoming solar radiation. However, at higher glacier elevations, the visible horizon can become much larger, in which case the extent must incorporate topographic features within visibility. For this study, a buffer of 5 km proved to be sufficient. For example, topographic shading was altered by less than 0.01 % when changing DEM extent from 5 to 3 km beyond the boundary of Satluj Glacier.
2.4 Idealized scenarios and regional analysis
We implement two idealized scenarios in order to test the sensitivity of the shaded relief and cast shadows to changes in overall glacier aspect and latitude. The components of topographic shading are calculated for two different glaciers as they are rotated in each of the main cardinal direction (north, east, south, and west). This allows us to observe changes in direct irradiance due to different valley aspects for the two glaciers. We then calculate the relative change in irradiance due to topographic shading across varying degrees of latitude (20–50∘) for the same two glaciers. Glacier size, slope, and surrounding topography are constant in these idealized scenarios, while aspect and latitude are systematically varied.
We also apply our cast shadow model to four glaciated regions across the greater Himalaya, shown in Fig. 2. These regions span multiple latitudes and degrees of topographic relief, and include a larger sampling of glacier geometries throughout HMA. Only glaciers larger than 3 km2 were used in the analysis in order to exclude small cirque glaciers and focus on valley glaciers with a developed tongue. These glaciers are then grouped based on general valley aspect of the ablation zone (ice below mid-elevation), as we are most interested in the cast shadowing effect from the valley walls along lower elevations where melt is dominant. The valley aspect for each glacier is determined based on the mode of pixels of a reclassified aspect value. They are then grouped into two categories: north/south- and east/west-oriented glaciers. Glaciers with less than 10 % majority aspect are manually corrected and labeled based on visual inspection. This introduces some complication as glacier aspect and morphology can be extremely irregular throughout the lower elevation for these HMA glaciers. For this reason, we include a large sample of valley glaciers for each region, ranging from 80 to 117 glaciers. A single mean value of change in solar radiation due to topographic shading is calculated across the defined ablation zone of each glacier. A kernel density estimation is fit to the mean values in each region for both north/south and east/west glaciers in order to see how the distribution of each group varies from one another.
3.1 Topographic impacts on individual glaciers
We selected a glacier in the Panjnad basin of the Indus watershed in the Himachal Pradesh region of the western Himalaya and one located in the eastern Himalaya on the China–Bhutan border for our detailed analysis and idealized scenarios. We refer to the glacier in the western Himalaya as Satluj Glacier, due to the subbasin in which it resides. Similarly, we refer to the glacier in the eastern Himalaya as Nianchu Glacier, after its subbasin name. We chose these two valley glaciers because they both have clear north-facing aspects and well-developed glacier tongues. However, Satluj Glacier is in an area of steep topography and high relief, while Nianchu Glacier spans a slightly higher range of elevation and is surrounded by less topographic relief.
3.1.1 Satluj Glacier
We calculate daily mean change in irradiance due to each topographic component averaged throughout the summer melt season (1 April–31 September). Figure 4 shows a smoothing spline of the mean change in irradiance due to each topographic component and their totals across elevation for Satluj Glacier. The spatial variability across the glacier surface is also included for visual aid (Fig. 4a–d). The mean change in irradiance for all combined topographic components is greatest at the lowest elevations (<4800 m), where cast shadowing is the largest, and at higher elevations (5600 m), where the impact of slope and aspect is largest. Cast shadowing only plays a significant role where the surrounding terrain is steep, close in proximity, and large enough to cast a significant shadow over the valley. For this particular glacier, this occurs at the lower elevations of the ablation zone. By comparison, slope and aspect tend to be important across all elevations but become slightly more significant as elevation increases. The effects of shaded relief on irradiance also increase with increasing elevation.
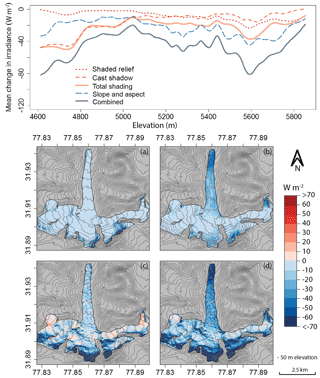
Figure 4Satluj Glacier. Mean change in irradiance throughout the summer melt season due to shaded relief (a), cast shadowing (b), slope and aspect (c), and combined topographic components (d). A smoothing spline was fit to the irradiance change values along the elevation profile of the glacier. The effect of cast shadowing appears to be more significant than that of shaded relief and slope and aspect at lower elevations where ablation dominates during the melt season.
Above 5050 m, the glacier cirque spreads out to incorporate various aspects. These aspects receive more direct solar radiation than their north-facing counterparts (Fig. 4c–d). Additionally, the mean change in irradiance from cast shadowing significantly decreases in both the east- and west-facing aspects, but not on a small south-facing tributary (Fig. 4b – right side). Change in irradiance on glacier ice less than 5050 m is clearly dominated by cast shadowing. This result is critical, as an overestimation of net shortwave radiation in the ablation zone (i.e., where the energy budget is frequently already positive) will have a larger effect on glacier mass balance than an overestimation in the accumulation zone (i.e., where the energy budget is usually negative enough that a small increase in incoming energy likely will not result in significant melt). Furthermore, Fig. 4 shows that the influence of topographic shading is also more significant than the mean change in irradiance from slope and aspect throughout the ablation zone. However, this is not true when comparing the effects of slope and aspect with shaded relief alone. These results emphasize the importance of correctly incorporating both methods of topographic shading when modeling solar radiation or surface energy balance, particularly for north-facing valley glaciers in areas of high relief.
3.1.2 Nianchu Glacier
Figure 5 shows an overall increasing mean change in irradiance from combined topographic components with increasing elevation for Nianchu Glacier. Both shaded relief and slope and aspect follow a similar trend of increasing mean change in irradiance with elevation, similar to Satluj Glacier. However, in contrast to Satluj Glacier, cast shadowing on Nianchu Glacier tends to have only a slightly larger effect than slope and aspect at elevations below 5500 m.
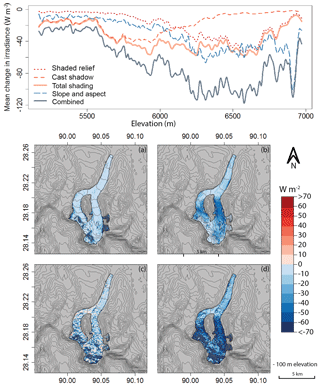
Figure 5Nianchu Glacier. Mean change in irradiance throughout the summer melt season due to shaded relief (a), cast shadowing (b), slope and aspect (c), and combined topographic components (d). A smoothing spline was fit to the irradiance change values along the elevation profile of the glacier. The effect of cast shadowing is largest at mid-elevations and occurs once Nianchu Glacier becomes more directly north-facing and is constricted between steep valley walls.
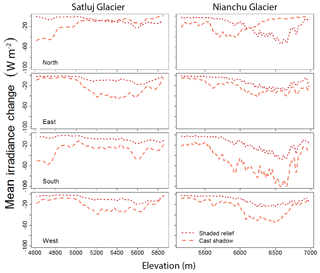
Figure 6Idealized scenarios for Satluj and Nianchu glaciers. Mean change in irradiance throughout the summer melt season due to shaded relief and cast shadows. Glaciers have been rotated in the four main cardinal directions to observe how shading changes with differing valley aspect. The difference between shaded relief and cast shadows is largest at lower and mid-elevations for the north and south valley direction. Also note that shaded relief is only greater than cast shadowing in the upper elevations of the north-facing direction for both glaciers.
The lower impact from cast shadows on the lower elevations for Nianchu Glacier is due to lower relief from the surrounding valley walls alongside the glacier toe, as well as the slightly northeastern direction of the valley. Sunrise occurs further northeast during the summer months than during the rest of the year; if the valley faces this direction and is surrounded by lower relief, the effect from cast shadowing can be minimal. Once above 5500 m, cast shadowing increases dramatically (Fig. 5) and then gradually decreases again at higher elevations. This shadowing can be seen in Fig. 5b, at the point at which the glacier divides into two tributaries and becomes more north-facing. Although Nianchu Glacier shows how variable topographic shading can be, shading is still a significant influence on the overall mean change in irradiance at the surface, even surpassing the impact of slope and aspect at certain elevations. However, because topography is highly variable and differs significantly from one basin to the next, the effects of topographic shading are equally heterogeneous.
3.2 Idealized scenarios
We perform idealized scenarios in order to quantify how topographic shading changes over different valley aspects and latitudes. In particular, we rotate Satluj and Nianchu glaciers in each of the main cardinal directions and move each glacier across varying degrees of latitude.
Only slight changes in the shaded relief occur when Satluj Glacier is rotated in each cardinal direction. On the other hand, cast shadowing shows a significant mean decrease in irradiance at lower elevations for both north and south valley aspects, compared to east and west (Fig. 6). This is expected, as shading is largest when the sun is low in the sky and nearby topography is oriented such that it blocks direct solar rays. This occurs during the early and late hours of the day when large terrain features are situated to the east and west. East and west valley aspects lose the orientation of steep adjacent topography able to cast significant shadows; thus the impact is greatly reduced. However, we see an increase in cast shadowing in the upper elevations for east and west aspects, as the upper tributaries in Fig. 4 are now predominantly facing north and south.
Nianchu Glacier shows a less clear pattern in aspect sensitivity; however, some differences are notable. Cast shadowing appears to be most significant for lower and mid-elevations with north and south valley aspects (Fig. 6). Additionally, the upper elevations for the south direction show a large increase in cast shadows. Shaded relief also shows a larger mean change in upper elevations for north and south directions. One interesting point when comparing both glaciers side by side is that the impact of shaded relief only surpasses cast shadowing in the north-facing direction. Additionally, in these scenarios, cast shadows and combined shading are largest when the glaciers are in a south-facing valley.
In general, we see that topographic shading is more significant on glaciers with a north or south valley aspect, particularly in the lower elevations of valley glaciers. This is of particular interest for regions like the Himalayas where valley glaciers are dominantly north- or south-facing. Although we continue to see variability in shading specific to each glacier, this general result can be a useful proxy to determine how impactful shading might be on a given glacier.
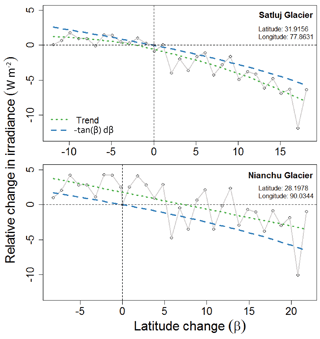
Figure 7Idealized scenarios for Satluj and Nianchu glaciers. Relative change in mean irradiance due to topographic shading as glacier is moved up and down in latitude, both spanning latitude from 20 to 50∘. Mean values are connected (grey) to show stochasticity. The overall trend (green dotted line) shows that the effects of shading increase with increasing latitude (β). The relative change mirrors the function −tan(β)dβ (blue dashed), which underestimates the relative change for Satluj Glacier and overestimates that for Nianchu Glacier.
When moving these same glaciers across varying degrees of latitude, we see a relative decrease in mean irradiance with increasing degree of latitude for both Satluj and Nianchu glaciers (Fig. 7). The trend of relative change in mean irradiance for each glacier closely follows a simple mathematical trend of negative tangent of the change in degree latitude (β), −tan(β)dβ. This mathematical trend arises from a simple trigonometric relationship between the zenith angle (Z) and length of cast shadows (S) for topography of a given height (H). As the zenith angle increases, the length of shadows cast also increases; . Apart from variation over the course of a day, zenith angles increase proportionally to an increase in latitude (Iqbal, 1983). As such, we assume that the change in irradiance from cast shadows across changing latitude, for a glacier with fixed topography, is largely a function of −tan(β)dβ, with variation based on changes in the intersection of azimuth angles and surrounding topography. While this simple mathematical trend captures the overarching changes in irradiance at differing latitudes, it overpredicts for Satluj Glacier and underpredicts for Nianchu Glacier.
3.3 Regional analysis
Outside of latitude and aspect, the impact of topographic shading is determined by combined characteristics of the immediate surrounding topography. As such, unique basin morphology gives rise to significant variability in the impacts of shading on direct solar radiation across glaciated regions. We apply the topographic models to the full Satluj basin including the surrounding glacial valleys, seen in Fig. 8. This expanded view offers a variety of valley aspects and different morphologies, and a means to explore the spatial variability in the shading components. A hillshade is used to visually enhance topography.
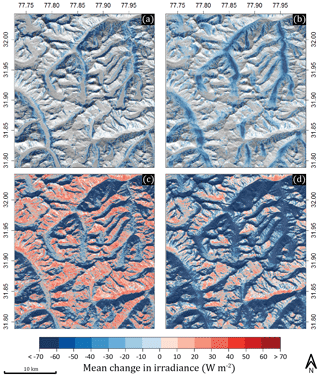
Figure 8Expanded view of the Satluj basin including surrounding glacial valleys of various orientation and aspect. Mean change in irradiance due to shaded relief (a), cast shadows (b), slope and aspect (c), and combined topographic components (d) is compared. Cast shadows show to be most influential in north- and south-facing valleys and can even offset the increase in irradiance due to slope and aspect for some south-facing valleys. Changes less than ±10 W m−2 are not shown.
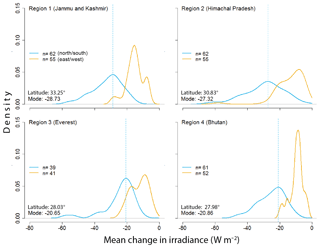
Figure 9Regional analysis spanning glaciated basins throughout the greater Himalaya of HMA. A mean value for change in irradiance due to cast shadowing is calculated for the ablation zone of each glacier within each region. We see that the distribution for north/south glaciers are more impacted by cast shadowing than east/west glaciers. Only values below mean glacier elevation were used to calculate the mean change for each glacier. Additionally, we see that the peak value for mean change in irradiance is greater in regions of higher latitudes (regions 1 and 2).
Shaded relief (Fig. 8a) appears to be significant only on extremely steep terrain that is not south-facing. Although this may be a significant topographic component in the upper cirques of some glaciers, the impact is minimal in glacier valleys and does not play a large role in the ablation zones where differences in solar irradiance can impact the mass balance. Cast shadows (Fig. 8b), on the other hand, are most pronounced in low-elevation north- and south-facing valleys, as predicted in our aspect sensitivity tests. Interestingly, although the mean change in irradiance increases due to slope and aspect for some south-facing valleys (Fig. 8c), this effect is offset, and in some cases overwhelmed, by cast shadows (Fig. 8d). By calculating the influence of these topographic components on a larger scale, we are able to confirm the results from our aspect sensitivity analysis in Fig. 6. Spatial patterns throughout the basin show that cast shadows significantly impact mean daily irradiance along deep north and south valley aspects.
We also apply these models to four glaciated regions spanning large portions of the greater Himalaya (Fig. 2), to further test our idealized scenarios and assess the degree of spatial variability in shading on valley glaciers. Again, we see that north/south-facing glaciers are more impacted by cast shadowing than east/west-facing glaciers (Fig. 9). Additionally, we see that the peak values in our north/south distributions (mode) of solar irradiance changes show a greater change in regions of higher latitude and relief (regions 1 and 2), fluctuating from a mean glacial change of −28.7 W m−2 at the highest latitude to −20.7 W m−2 at the lowest. Although we see significant variability between regions, there is generally less spread for east/west- than north/south-facing glaciers. Our regional model validates the findings in our idealized scenarios, confirming that the impact of topographic shading is more prominent on north- and south-facing valleys with a general increase in the mean change in irradiance between regions located at higher latitudes.
The results of our topographic shading model highlight the important role of topography on the direct clear-sky solar radiation. However, because our results rely heavily on simulating topography from digital elevation models, we are limited by the accuracy and resolution of these DEMs. Although this does not diminish our results, we recognize the value in assessing the variability and uncertainty associated with using differing DEM products and higher resolution. Additionally, our results motivate further investigation into the relationship between topography and additional components of both global radiation and energy balance. Finally, the results here are potentially relevant for quantifying the sensitivity of glacier mass balance to climate change.
4.1 DEM accuracy and resolution
ASTER GDEM, used in this study, builds surface elevation using orthorectification of two ASTER images, producing a product near 30 m resolution. Although ASTER provides greater detail and generally good elevation accuracy, orthorectification tends to fail in completely snow-covered regions as orthoimages become difficult to align. These issues, along with the resolution, introduce some inaccuracy as flat surface features become exaggerated and ridgelines are smoothed, which can artificially increase or lower the effects of shading from topographic features (Arnold et al., 2006). It should also be noted that, although the sampling interval of the GDEM is 30 m resolution, the spatial resolution may be up to 3 times coarser in some regions (Hengl and Reuter, 2011). Despite the shortcomings of this DEM product, the findings in this study still demonstrate clearly the impacts of DEM resolution on incoming shortwave radiation.
Hopkins et al. (2010) found a linear increase in modeled glacier melt as DEM resolution decreases from 1 to 1000 m. This is due to decreased textural relief as DEM resolution is reduced. In certain scenarios, Hopkins et al. found that total melt increased with DEM resolution by 4 %. In order to illustrate the potential impact of DEM resolution on topographic shading, we calculate a mean glacial change in irradiance as we systematically decrease the ASTER GDEM resolution. Figure 10 shows a significant decrease in accurately calculating topographic shading as resolution declines for Satluj and Nianchu glaciers. As resolution coarsens, the modeled mean glacial change in irradiance abruptly decreases (a nearly 17 % loss for Nianchu Glacier as resolution increases from 30 m to ∼100 m) and continues to steadily decrease for both glaciers until the modeled change in irradiance is nearly 50 % below the initial level. Topographic shading, particularly from cast shadowing, relies on the ability to simulate a change in energy based on detailed features of the surrounding topography. As detail degrades, so does the true effect of topographic shading. Higher-resolution and higher-accuracy DEMs, therefore, will significantly improve the accuracy of the shading models. This begs the question as to whether the impact of modeled shading would continue to increase at the same rate when using DEM resolutions higher than 30 m.
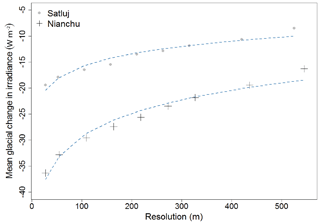
Figure 10The effect of decreasing resolution on the change in irradiance due to topographic shading for Satluj and Nianchu glaciers. The mean change in irradiance appears to decrease with the natural log of resolution (blue line). Although this does not fully describe the relationship observed, it aids in highlighting the non-linear change in irradiance with respect to resolution. This is due to smoothing topography as resolution decreases.
4.2 Diffuse and terrain-reflected radiation
We focus specifically on direct solar radiation in this study, which is the major component of the global radiation. However, other global radiation terms are also impacted by topography. While surrounding topography decreases the amount of direct clear-sky irradiance received at the surface, diffuse sky radiation (Ds) and reflected radiation from surrounding terrain (Dt) can also alter the net global radiation. For example, Arnold et al. (2006) calculates the total diffuse radiation as
where reflected radiation from surrounding topography (Dt) is calculated as
where αt is the mean albedo of the surrounding terrain, Fs is the sky-view factor, and Qglobal is measured global radiation. From Eqs. (7) and (8), it is apparent that diffuse sky and terrain-reflected radiation have an inverse relationship with the sky-view factor, which is directly related to the height of the surrounding topography. As such, we would expect the effects of these two components of global radiation to somewhat offset one another in the presence of topography. In Eq. (2), daily mean direct solar radiation decreases in the presence of higher topography; diffuse sky will also decrease as the view factor decreases, and terrain-reflected radiation will increase the radiation received at the surface.
Depending on the orientation of topography, local meteorological conditions, and the mean albedo of the surrounding terrain, terrain-reflected radiation could significantly offset the effects of topographic shading on global radiation received on a glacier surface. The relationship between direct, diffuse sky, and terrain-reflected radiation should be further investigated, especially for valley glaciers in steep terrain.
4.3 Glacier response to climate change
Most glaciers, under current trends of increasing global temperature, are expected to thin and retreat in response. As they do so, they will thin and retreat into varying amounts of topographic shading. For example, Satluj Glacier will likely thin and retreat up-valley. However, this response may be dampened somewhat by the decrease in incoming solar radiation as a portion of the ablation zone resides in the area of maximum shading (Fig. 4). Ultimately, once the glacier tongue has receded beyond the most shaded region in Fig. 4, the ablation zone will receive a higher amount of direct solar radiation and the mass loss will increase. The link between climate, glacier dynamics, and shading is also relevant for Nianchu Glacier. As the ablation zone moves up-valley into regions of increased shading, the surface will be less affected by direct solar radiation throughout the day, reducing the melt rate and dampening the response to changes in climate. These scenarios suggest that shading may not only be a useful tool for improving our understanding of the current mass balance of valley glaciers throughout HMA but could also likely improve our understanding of the magnitude of glacier response to climatic change under future-climate scenarios. Similarly, the variability in shading on a glacier surface over time is likely to play a role in explaining glacier sensitivity to historical climate changes. Future work should focus on quantifying the role of topographic shading in glacier response to climate changes.
Topographic shading is comprised of two components: shaded relief and cast shadows. Shaded relief is due to slope and aspect and occurs when a surface is blocked from the sun's rays due to its own relief. Cast shadows occur when solar rays project shadows from one topographic feature onto another, which occurs commonly in valleys surrounded by steep valley walls.
We create a topographic solar radiation model in order to quantify the effects of topographic shading on valley glaciers with a variety of aspects and latitudes, and within a range of terrain settings. We find that potential direct clear-sky solar radiation on a glacier surface can be significantly affected by shading in regions of steep topography and high relief such as is common in HMA. Overall, there is an increase in shaded relief with increasing elevation, as slope angles generally become steeper. In contrast, cast shadowing does not show any clear trend with elevation; rather, it appears to be controlled by the distance and direction of the immediate surrounding topography, as well as size of nearby terrain. This makes cast shadowing extremely variable along and between glacier valleys. Importantly, we see that cast shadowing can account for a significant decrease in irradiance in the glacier ablation zone. Indeed, cast shadowing is typically the dominant mechanism contributing to total shading in all but the steepest of slope angles; as such, it should be incorporated in energy balance models.
We find that glaciers with north and south valley aspects are generally more influenced by cast shadowing. Additionally, we see a general increase in shading with increasing latitude. This suggests that parameters such as latitude, aspect, and slope may be useful in predicting the overall effect of shading for a particular glacier. This could be useful in estimating the impact of shading on a regional scale in order to incorporate the full impact of topography in large-scale models. Furthermore, DEM spatial resolution noticeably alters the modeled accuracy of topographic shading on a glacier's surface.
We show that topographic shading results in a significant mean change in irradiance, particularly in the ablation zone of north- and south-facing valley glaciers. This implies that topographic shading has the potential to greatly impact the surface energy balance of Himalayan glaciers during the summer melt season and could also be useful in understanding different glacier mass balance estimates throughout HMA.
All input data are publicly available. Model code can be found at https://doi.org/10.5281/zenodo.1948620 (Olson, 2018).
Both authors defined the problems and motivation for this study. MO developed the code and performed the analysis. The paper was prepared by MO with contributions and edits from SR.
The authors declare that they have no conflict of interest.
We acknowledge the support for this research through funding awarded to
Summer Rupper (NSF EAR 1600587 and NASA 15-HMA15-0030). We also acknowledge
the valuable constructive feedback from Rick Forster and Simon Brewer, as
well as Eric Johnson, Jewell Lund, and others from the University of Utah.
Edited by: Christian Haas
Reviewed by: Geoff Evatt and one anonymous referee
Aguilar, C., Herrero, J., and Polo, M. J.: Topographic effects on solar radiation distribution in mountainous watersheds and their influence on reference evapotranspiration estimates at watershed scale, Hydrol. Earth Syst. Sci., 14, 2479–2494, https://doi.org/10.5194/hess-14-2479-2010, 2010.
Arendt, A., Bolch, T., Cogley, G., Gardner, A., Hagen, J. O., Hock, R., Kaser, G., Paul, F., Radic, V., Bliss, A., Fountain, A., Mercer, A., Negrete, A., Giffen, B., Menounos, B., Kienholz, C., Mayer, C., Nuth, C., Burgess, D., Hall, D., Kriegel, D., Berthier, E., Burgess, E., Cawkwell, F., Wyatt, F., Hartmann, G., Wolken, G., Frey, H., Brown, I., Howat, I., Lund, J., Rich, J., Fil- bert, K., Andreassen, L., Copland, L., Beedle, M., Koenig, M., Sharp, M., Moelg, N., Sigurdsson, O., Rastner, P., Forester, R., LeBris, R., Pettersson, R., Wheate, R., Herreid, S., Voro- gushin, S., Winsvold, S., Chinn, T., Hagg, W., and Manley, W.: Randolph Glacier Inventory 1.0: a Dataset of Global Glacier Outlines, Global Land Ice Measurements from Space, Boulder Colorado, USA Digital Media, 2015.
Arnold, N. S., Rees, W. G., Hodson, A. J., and Kohler, J.: Topographic controls on the surface energy balance of a high Arctic valley glacier, J. Geophys. Res., 111, F02011, https://doi.org/10.1029/2005JF000426, 2006.
Bajracharya, S. R. and Shrestha, B. R.: The status of glaciers in the Hindu Kush-Himalayan region. International Centre for Integrated Mountain Development (ICIMOD), 2011.
Chen, X., Su, Z., Ma, Y., Yang, K., and Wang, B.: Estimation of surface energy fluxes under complex terrain of Mt. Qomolangma over the Tibetan Plateau, Hydrol. Earth Syst. Sci., 17, 1607–1618, https://doi.org/10.5194/hess-17-1607-2013, 2013.
Corripio, J. G.: Vectorial algebra algorithms for calculating terrain parameters from DEMs and solar radiation modelling in mountainous terrain, Int. J. Geogr. Inf. Sci., 17, 1–23, 2003.
DeBeer, C. M. and Sharp, M. J.: Topographic influences on recent changes of very small glaciers in the Monashee Mountains, British Columbia, Canada. J. Glaciol., 55, 691–700, 2009.
Dozier, J.: A clear-sky spectral solar radiation model for snow-covered mountainous terrain, Water Resour. Res., 16, 709–718, 1980.
Dozier, J. and Frew, J.: Rapid calculation of terrain parameters for radiation modeling from digital elevation data, IEEE T. Geosci. Remote Sens., 28, 963–969, 1990.
ESRI Basemap: National Geographic, Esri, DeLorme, HERE, UNEP-WCMC, TomTom, Intermap, Increment p Corp., GEBCO, USGS, NASA, ESA, METI, FAO, NPS, NRCAN, NOAA, iPC, GeoBase, IGN, Kadaster NL, Ordinance Survey, Esri Japan, Esri China (Hong Kong), March 2017.
Greuell, W. and Smeets, P.: Variations with elevation in the surface energy balance on the Pasterze (Austria), J. Geophys. Res., 106, 31717–31727, 2001.
Han, C., Ma, Y., Chen, X., and Su, Z.: Estimates of land surface heat fluxes of the Mt. Everest region over the Tibetan plateau utilizing ASTER data, Atmos. Res., 168, 180–190, 2016.
Hengl, T. and Reuter, H., : How accurate and usable is the GDEM? A statistical assessment of the GDEM using LiDAR data, Geomorphometry, 2, 45–48, 2011.
Hock, R.: A distributed temperature-index ice-and snowmelt model including potential direct solar radiation, J. Glaciol., 45, 101–111, 1999.
Hopkinson, C., Chasmer, L., Munro, S., and Demuth, M. N.: The influence of DEM resolution on simulated solar radiation-induced glacier melt, Hydrol. Process., 24, 775–788, 2010.
Immerzeel, W. W., Van Beek, L. P., and Bierkens, M. F.: Climate change will affect the Asian water towers, Science, 328, 1382–1385, 2010.
Iqbal, M.: An introduction to solar radiation, Academic Press Inc., New York, NY, 14–16, 1983.
Klok, E. J. and Oerlemans, J.: Model study of the spatial distribution of the energy and mass balance of Morteratschgletscher, Switzerland, J. Glaciol., 48, 505–518, 2002.
Kumar, L., Skidmore, A. K., and Knowles, E.: Modelling topographic variation in solar radiation in a GIS environment, Int. J. Geogr. Inf. Sci., 11, 475–497, 1997.
Munro, D. S. and Young, G. J.: An operational net shortwave radiation model for glacier basins, Water Resour. Res., 18, 220–230, 1982.
Oerlemans, J. and Klok, E. J.: Energy balance of a glacier surface: analysis of automatic weather station data from the Morteratschgletscher, Switzerland, Arct. Antarct. Alp. Res., 34, 477–485, 2002.
Olson, M.: mattols/TopoSol: First release of topographic forcing model (Version v1.0), Zenodo, https://doi.org/10.5281/zenodo.1948620, 2018.
Pandey, P., Ali, S. N., Ramanathan, A. L., and Venkataraman, G.: Regional representation of glaciers in Chandra Basin region, western Himalaya, India, Geosci. Front., 8, 841–850, 2017.
Plummer, M. A. and Phillips, F. M.: A 2-D numerical model of snow/ice energy balance and ice flow for paleoclimatic interpretation of glacial geomorphic features, Quaternary Sci. Rev., 22, 1389–1406, 2003.
Vaughan, D. G., Comiso, J. C., Allison, I., Carrasco, J., Kaser, G., Kwok, R., Mote, P., Murray, T., Paul, F., Ren, J., Rignot, E., Solomina, O., Steffen K., and Zhang, T.: Observations: Cryosphere, in: Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, UK and New York, NY, USA, 2014.
Way, R. G., Bell, T., and Barrand, N. E.: An inventory and topographic analysis of glaciers in the Torngat Mountains, northern Labrador, Canada, J. Glaciol., 60, 945–956, 2014.
Williams, L. D., Barry, R. G., and Andrews, J. T.: Application of computed global radiation for areas of high relief, J. Appl. Meteorol., 11, 526–533, 1972.
Zhang, S., Li, X., and Chen, Y.: Error assessment of grid-based direct solar radiation models, Int. J. Geogr. Inf. Sci., 29, 1782–1806, 2015.





