the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Version 2 of the EUMETSAT OSI SAF and ESA CCI sea-ice concentration climate data records
Atle Macdonald Sørensen
Stefan Kern
Rasmus Tonboe
Dirk Notz
Signe Aaboe
Louisa Bell
Gorm Dybkjær
Steinar Eastwood
Carolina Gabarro
Georg Heygster
Mari Anne Killie
Matilde Brandt Kreiner
John Lavelle
Roberto Saldo
Stein Sandven
Leif Toudal Pedersen
We introduce the OSI-450, the SICCI-25km and the SICCI-50km climate data records of gridded global sea-ice concentration. These three records are derived from passive microwave satellite data and offer three distinct advantages compared to existing records: first, all three records provide quantitative information on uncertainty and possibly applied filtering at every grid point and every time step. Second, they are based on dynamic tie points, which capture the time evolution of surface characteristics of the ice cover and accommodate potential calibration differences between satellite missions. Third, they are produced in the context of sustained services offering committed extension, documentation, traceability, and user support. The three records differ in the underlying satellite data (SMMR & SSM/I & SSMIS or AMSR-E & AMSR2), in the imaging frequency channels (37 GHz and either 6 or 19 GHz), in their horizontal resolution (25 or 50 km), and in the time period they cover. We introduce the underlying algorithms and provide an evaluation. We find that all three records compare well with independent estimates of sea-ice concentration both in regions with very high sea-ice concentration and in regions with very low sea-ice concentration. We hence trust that these records will prove helpful for a better understanding of the evolution of the Earth's sea-ice cover.
Satellite-retrieved records of Arctic and Antarctic sea-ice concentration differ widely in their estimates of a specific sea-ice concentration on a given day in a given region (e.g. Ivanova et al., 2015; Comiso et al., 2017a). Integrated over the entire Arctic, these differences accumulate up to a 20 % uncertainty in the long-term trends of sea-ice extent and sea-ice area (Comiso et al., 2017b), which hinders a robust evaluation and bias correction of climate models, and in particular hinders a robust estimate of the future evolution of the Arctic sea-ice cover. For example, Niederdrenk and Notz (2018) found that observational uncertainty is the main source of uncertainty for estimating at which level of global warming the Arctic will lose its summer sea-ice cover. This is because both the bias correction of large-scale climate models and the extrapolation of observed relationships between forcing and sea-ice coverage can only be carried out robustly if observational uncertainty is sufficiently small. In this contribution, we introduce three new climate data records of gridded global sea-ice concentration that address some of the shortcomings of existing records, and in particular provide additional information that allows users to judge the robustness of the sea-ice concentration estimates.
Our focus on sea-ice concentration is to a substantial degree driven by the fact that information on sea-ice concentration is key to the vast majority of approaches for understanding the changing sea-ice cover of our planet. This importance of sea-ice concentration derives both from the availability of a long, continuous record of the underlying passive-microwave data and from the central importance of sea-ice concentration for many physical processes connected to the sea-ice cover. For example, the albedo of the polar oceans is strongly influenced by sea-ice concentration (e.g. Brooks, 1925), as is much of the heat and moisture transfer between the ocean and the atmosphere (e.g. Maykut, 1978).
Information on sea-ice concentration is also used to derive total sea-ice area or extent. In the Arctic the latter has been found to be linearly related to global-mean temperature (e.g. Gregory et al., 2002; Niederdrenk and Notz, 2018), atmospheric CO2 concentration (e.g. Johannessen, 2008; Notz and Marotzke, 2012) and anthropogenic CO2 emissions (Zickfeld et al., 2012; Herrington and Zickfeld, 2014; Notz and Stroeve, 2016). These linear relationships allow one to estimate the future evolution of Arctic sea ice directly from the observational record (e.g. Notz and Stroeve, 2016; Niederdrenk and Notz, 2018), to evaluate the sea-ice evolution in coupled climate models, and to bias correct estimates from climate models for improved projections of the future sea-ice cover (e.g. Mahlstein and Knutti, 2012; Screen and Williamson, 2017; Sigmond et al., 2018). For any of these applications, the reliability of the underlying sea-ice concentration record is crucial.
This importance of a reliable sea-ice concentration record is also reflected in the definition of sea-ice essential climate variables (ECVs) by the Global Climate Observing System (GCOS), a body of the World Meteorological Organization (WMO). In their most recent update (GCOS-IP, 2016), they request that reliable observational records of sea-ice concentration are made available to the climate research community. However, the reliability and long-term stability of existing records is often not clear. This is, for example, reflected by substantial differences between existing estimates of sea-ice concentration from various algorithms (e.g. Ivanova et al., 2015; Comiso et al., 2017b).
With our three new climate data records of sea-ice concentration we aim to provide the users with new reference data sets that have three clear advantages over most existing records. First, all our three records provide quantitative information on uncertainty and access to filtered as well a raw values at every grid point and every time step. Second, they are based on dynamic tie points, which capture the time evolution of surface characteristics of the ice cover and help to minimize the impact of sensor drift and change in satellite sensor. Third, they are produced in the context of sustained services offering committed extension, documentation, traceability, and user support.
The first of our three climate data records (CDRs) is referred to as OSI-450. It is based on coarse-resolution (30–60 km) passive microwave (PMW) satellite data that are available from October 1978 onwards. These data are also at the heart of the two currently most widely used sea-ice concentration algorithms, namely the NASA Team algorithm (Cavalieri et al., 1984) and the bootstrap algorithm (Comiso et al., 2017b). OSI-450 has been released by the European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT) Ocean and Sea Ice Satellite Application Facility (OSI SAF, http://www.osi-saf.org/, last access: 15 June 2018) and is a fully revised version of its predecessor OSI-409 (Tonboe et al., 2016). The second and third CDRs are called SICCI-25km and SICCI-50km. They are based on medium-resolution (15–25 km) PMW satellite data available from June 2002 onwards. These two SICCI CDRs are released by the European Space Agency (ESA) Climate Change Initiative (CCI, http://cci.esa.int/, last access: 15 June 2018) programme.
Table 1Summary of the three SIC CDRs presented in this paper. The values entered in the table are all described in the course of the paper.
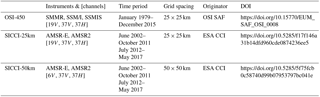
Table 2Platform, instrument, and time period for input brightness temperatures used in the sea-ice data records. All frequencies listed have both horizontal and vertical polarization channels.
All three sea-ice concentration (SIC) CDRs share the same algorithms, processing chains, and data format. In particular, they were all developed with their primary application as climate-data records in mind, putting very narrow constraints on the permissible long-term drift of the records. As such, the underlying algorithms are based on earlier work by the European sea-ice remote-sensing community (Andersen et al., 2007; Tonboe et al., 2016) and provide sea-ice concentration estimates with (a) low sensitivity to atmospheric noise including liquid water content and water vapour, (b) low sensitivity to surface noise including wind roughening of the ocean surface, and variability of sea-ice emissivity and temperature, (c) the capability to adjust to the climatological changes in the above-mentioned noise sources, and (d) a quantification of the remaining noise at each time step for each pixel. Together, the three new climate-data records are a unique joint contribution of the two leading European Earth Observation agencies for addressing the requirements of the climate research community and climate information services. The three CDRs are summarized in Table 1, and the satellite data used as input are in Table 2. The values in Tables 1 and 2 will all be introduced in the course of the paper.
In this contribution, we outline the underlying algorithms and the philosophy behind them. We also provide an evaluation of the resulting climate-data records. We start in Sect. 2 by describing the satellite and ancillary data used as input. Section 3 describes the algorithms and processing steps implemented to process the data records. Afterwards, Sect. 4 is devoted to the resulting data records, their evaluation results, and known limitations. Discussion, outlook, and conclusions are covered in Sect. 5.
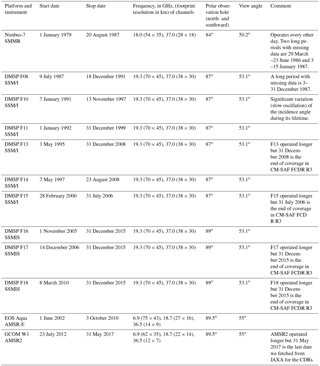
This section summarizes the satellite as well as the numerical weather prediction (NWP) data used in the climate data records. Each of these data sources are fully described in dedicated technical documentation, web resources, and scientific literature, so that we provide only the key information directly relevant to the discussion in this paper. Figure 1 shows the temporal coverage of the data sources entering the three SIC CDRs. Two ESA CCI data records (grey box marked “ESA CCI (2×)”) are based on the Advanced Microwave Scanning Radiometer – Earth Observing System (AMSR-E) and AMSR2 instruments (orange and dark-orange horizontal bars), while the EUMETSAT OSI SAF data record (grey box marked “OSI SAF (OSI-450)”) is based on the Scanning Multichannel Microwave Radiometer (SMMR, purple bar), Special Sensor Microwave/Imager (SSM/I, dark-blue bars), and Special Sensor Microwave Imager / Sounder (SSMIS, light-blue bars) instruments on board the Defense Meteorological Satellite Program (DMSP) satellites. ERA-Interim reanalysis weather data from the European Centre for Medium-Range Weather Forecasts (ECMWF) are also used throughout the period (not shown). Overlap of satellite missions and the 9-month data gap between AMSR-E and AMSR2 operations are clearly visible from Fig. 1. Although there was always at least one satellite mission carrying a relevant passive microwave instrument after October 1978, a few data gaps exist in the satellite data record that are too short to appear in Fig. 1. The most prominent are documented in the “comments” column of Table 2 and extensive lists of missing dates are in the product user guides (PUGs) of the CDRs. These PUGs are always accessible from the data set landing pages (see DOIs in Table 1). Figure 1 also shows other related satellite missions that do not enter the new CDRs, but might be relevant for their future extension in a compatible Interim Climate Data Record (grey box marked “OSI SAF ICDR”). They are discussed in our Outlook, Sect. 5.2.
Figure 1Time-coverage diagram for the new ESA CCI and EUMETSAT OSISAF SIC CDRs. The ESA CCI CDR is based on medium-resolution AMSR-E and AMSR2 sensors, while the EUMETSAT OSISAF CDR uses the coarse-resolution SMMR, SSM/I, and SSMIS instruments. Other current and future passive microwave instruments, as well as the OSI SAF ICDRs, are discussed in our Outlook, Sect. 5.2.
2.1 Input satellite data
More details about the satellite instruments and platforms are given in Table 2. It lists the satellite platforms, sensors, and time periods for brightness temperatures (TB) used as input for the SIC CDRs. Some specific instrument characteristics like channel frequencies, spatial resolution, view angle and area covered by the polar observation hole are also documented there. Table 2 documents that the instrument series might have quite different characteristics (e.g. channel frequencies or incidence angle). Building a consistent data record requires methodologies that carefully intercalibrate and tune the algorithms to yield similar results when using all these sensors. This is the essence of the dynamic tuning approaches adopted in Tonboe et al. (2016) and further developed for the new CDRs (Sect. 3).
Building CDRs from this suite of satellite sensors is best achieved if the selected algorithms only use channels that are consistently available throughout the period. Slight changes in incidence angle or wavelengths between the sensor series can be compensated for by the algorithms, but it is harder or even impossible to achieve temporal consistency in the event of sudden loss of channels. In that respect, it is noteworthy that the 23.0 GHz channels of the SMMR instrument have been highly unstable since their launch, and eventually ceased to function on 11 March 1985 (Njoku et al., 1998). There is thus no continuous data record of brightness temperatures in the vicinity of the water vapour absorption line (22.235 GHz). Such a wavelength is typically used in filtering weather effects in other SIC CDRs (e.g. Meier et al., 2017). Our algorithms do not rely on such a channel (Sect. 3.4.2).
Although not identical, the spatial resolution of the channels needed for the SIC algorithms is similar for the three coarse-resolution sensor series (SMMR, SSM/I, and SSMIS) with about 70×45 km instantaneous field-of-view (iFoV) diameters for the 19 GHz frequency channels, and 38×30 km for the 37 GHz ones (Table 2). The two medium-resolution radiometers AMSR-E and AMSR2 have finer resolutions at these channels (27×16 km and 14×9 km), accompanied by increased sampling (10×10 km instead of 25×25 km for SSM/I). It is noteworthy that iFoV diameters, as reported in Table 2 and at several online resources, such as the WMO OSCAR Space-based Capabilities database, are not a measure of the true footprint of an individual measured pixel. This is because the iFoV takes into account neither the motion of the antenna (scan direction) nor the motion of the spacecraft (along its orbit) during the integration period needed to acquire a single pixel. The effective field-of-view (eFoV) diameter includes the two effects and is a better measure of the true footprint of the instrument. For example, the eFoV of the SSM/I 19 GHz channels is closer to 70×75 km. The dimensions of the iFoV and eFoV are referred to as the resolution of the channels. The sampling is how close in space the FoVs are acquired. Most channels are thus oversampled.
Two of the differences between the instrument series are the width of their observation swaths, and the inclination of their orbits. This translates into different extents of the polar observation hole, and no data are available for sea-ice monitoring north of 84∘ (SMMR), 87∘ (SSM/I), 89∘ (SSMIS), and 89.5∘ (AMSR-E and AMSR2).
For our data records, a newly reprocessed version of the SMMR, SSM/I, and SSMIS data into a Fundamental Climate Data Record (FCDR, L1) was accessed from the EUMETSAT Climate Monitoring Satellite Application Facility (CM-SAF, Fennig et al., 2017). In the FCDR, the TB are recomputed from Antenna Temperatures (TA), screened and corrected for known artefacts like solar intrusion, and intercalibrated between missions. The AMSR-E data we use are the NSIDC FCDR AE_L2A V003 FCDR by Ashcroft and Wentz (2013), covering the full lifetime of the mission from 1 June 2002 to 4 October 2011. For AMSR2, we use recalibrated (version 2) L1R data that we accessed directly from the Japan Aerospace Exploration Agency (JAXA), covering 23 July 2012 until 15 May 2017, that is the end of the SICCI-25km and SICCI-50km CDRs. For both AMSR-E and AMSR2, the TB are available both at their nominal resolution (documented in Table 2), and post-processed at lower resolution matching those of other channels (e.g. the 36.5 GHz TB at the resolution of the 6.9 GHz channel). We use the nominal resolution of the TB, not the resolution-matched ones. It is noteworthy that the AMSR2 data are not from an FCDR, but rather from an archive of an operational data stream. We use the data as they are provided by JAXA, without applying extra calibration towards AMSR-E (thus unlike Meier and Ivanoff, 2017) since our algorithms do not require such stringent calibration thanks to using dynamic tuning (Sect. 3.3).
2.2 ERA-Interim data
The microwave radiation emitted by the ocean and sea ice travels through the Earth's atmosphere before being recorded by the satellite sensors. Scattering, reflection, and emission in the atmosphere add or subtract contributions to the radiated signal, and challenge our ability to accurately quantify sea-ice concentration. An initial step in our processing is thus the explicit correction of the TBs for the atmospheric contribution to the top of the atmosphere radiation (see Sect. 3.4.1). For this purpose, we accessed the global 3-hourly fields from ECMWF's ERA-Interim reanalysis (Dee et al., 2011). Fields of 10 m wind speed, 2 m air temperature, and total column water vapour are used. The ERA-Interim reanalysis starts in January 1979 and is available throughout the time period of our CDRs. Unavailability of ERA-Interim data prior to 1979 made it impractical to use the earliest period of SMMR data (October to December 1978).
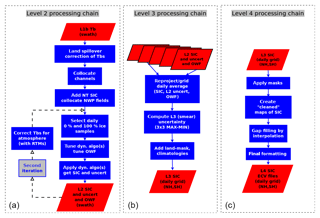
Figure 2From (a) to (c), the three main elements (Level 2, Level 3, and Level 4) in the sea-ice concentration (SIC) processing workflow. The red boxes depict data files, the blue boxes correspond to individual steps (a.k.a. algorithms) in the processing. The files that exit a processing chain (e.g. the “L2 SIC and uncert and OWF” at the bottom of the Level 2 processing chain) are the input for the next level of processing. Acronyms: NT is the Nasa Team algorithm, OWF is open-water filter, RTM is radiative transfer model, uncert stands for uncertainty, L2 is Level 2, L3 is Level 3, L4 and is Level 4.
This section introduces the algorithms and some processing elements that are used in the making of the SIC CDRs. In many cases, these algorithms are evolutions of those already applied in the previous version of the EUMETSAT OSI SAF CDR (OSI-409, Tonboe et al., 2016).
3.1 Overview of the processing chain
Figure 2 gives an overview of the processing chain for the three CDRs. The red boxes are data (stored in data files) and the blue boxes are processing elements that apply algorithms to the data. The whole process is structured into three chains, at Level 2 (left-hand side), Level 3 (middle), and Level 4 (right-hand side). The input Level 1 (L1) data files hold the fields observed by the satellite sensors at the top of the atmosphere, in satellite projection: the brightness temperatures (TB) are structured in swath files. The Level 2 (L2) chain transforms these into the environmental variables of interest, but still on swath projection: the SIC, its associated uncertainties, and flags. The L2 chain holds an iteration (marked by the “2nd iteration” grey box) similar to the workflow in Tonboe et al. (2016) and stemming from the developments of Andersen et al. (2006). This iteration implements two key correction schemes: the atmospheric correction algorithm at low-concentration range (Sect. 3.4.1) and a novel correction for systematic errors at high-concentration range (Sect. 3.4.3). The Level 3 (L3) chain collects the L2 data files and produces daily composited fields of SIC, uncertainties, and flags on regularly spaced polar grids. These fields can and will typically exhibit data gaps, e.g. in case of missing satellite data. The Level 4 (L4) chain fills the gaps, applies extra corrections, and formats the data files that will appear in the CDR.
The next subsections are devoted to giving some more details about the main features of the several algorithms involved.
3.2 A hybrid, self-tuning, self-optimizing sea-ice concentration algorithm
A new sea-ice concentration algorithm was developed during the ESA CCI Sea Ice projects and is used for the three CDRs. It is an evolution of the algorithms used in Tonboe et al. (2016). In this section, we describe both how the algorithm is trained to TB training data sets, and how it is then applied to actual TB measurements recorded by satellite sensors. The process of selecting training TB data is covered in Sect. 3.3.
We call the SIC algorithm a hybrid algorithm because it combines two other SIC algorithms: one that is tuned to perform better over open-water and low-concentration conditions (named BOW for best open water), and one that is tuned to perform better over closed-ice and high-concentration conditions (named BCI for best closed ice). The combination equation is quite simply a linear weighted average of BOW and BCI results, where wow is the open-water weight and SIC is expressed as sea-ice fraction [0; 1]:
OSI-409 already used a hybrid method. It combined the bootstrap frequency mode (BFM) algorithm (Comiso, 1986) as BOW, and the Bristol (BRI) algorithm (Smith and Barrett, 1994; Smith, 1996) as BCI. Andersen et al. (2007) and later Ivanova et al. (2015) confirmed that BFM (BRI) was so far the published algorithm, including NASA-Team and bootstrap, performing best at low (high) SIC conditions, and notably that BRI is more accurate at high concentration than the bootstrap polarization mode (BPM) algorithm. BFM and BPM are widely used for sea-ice monitoring in what is commonly known as the bootstrap algorithm (Comiso and Nishio, 2008). Smith (1996) introduces the BRI algorithm as a generalization of the BFM and BPM algorithms. BFM computes SIC values in the (19V, 37V) TB space and BPM in the (37V, 37H) TB space. BRI uses the three-dimensional (19V, 37V, 37H) TB space, where 19V (19H) is notation for “the channel with a frequency near 19 GHz and with vertical (horizontal) polarization”.
Figure 3 illustrates the functioning of the BFM algorithm. Comiso (1986) recognized that the typical signature of open-water (OW, SIC = 0 %, grey triangles) TB data clusters around an averaged point location (the OW tie point, H) in the (19V, 37V) TB space. Conversely, the closed-ice (CI, SIC = 100 %, grey discs) TB data mostly cluster along a line (the consolidated ice line A–D). Comiso (1986) thus designed a SIC algorithm wherein isolines of constant SIC are parallel to the A–D line and pass through the measured TB at point P. A geometric algorithm using the intersection of the (H, P) and (A, D) lines at point I returns the SIC value (in our example SIC = 68 %). In the same study, similar aggregation of typical TB signatures and a geometric algorithm were also used in the (37V, 37H) TB space (BPM algorithm). For easing later discussion, here we note that in winter Arctic conditions, the typical multi-year sea-ice signature is to the left of the ice line – close to D – while first-year sea ice and young sea ice is to the right – closer to A (Comiso, 2012). The AMSR-E TB samples in Fig. 3 are from Pedersen et al. (2018), the ESA CCI Sea Ice Round Robin Data Package (RRDP).
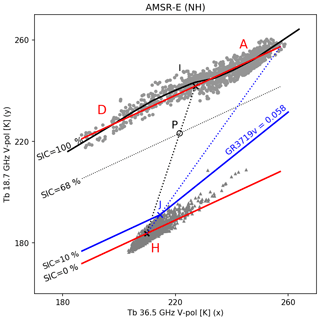
Figure 3Illustration of the bootstrap frequency mode (BFM, Sect. 3.2) and open-water filter (OWF, Sect. 3.4.2) algorithms in a 36.5V (x axis) and 18.7 GHz (y axis) TB space of AMSR-E (Winter NH conditions). The grey symbols are actual AMSR-E TB measurements over SIC = 0 % (triangles) and SIC = 100 % (disks) conditions, from Pedersen et al. (2018). The SIC = 100 % measurements fall generally along a line (the consolidated ice line), while the mean open-water signature is point H. An example measurement P (black circle) falling on the SIC = 68 % isoline illustrates the functioning of BFM. The blue solid and dotted lines illustrate the tuning and functioning of the OWF (as described in Sect. 3.4.2). The black solid curve fitting SIC = 100 % conditions illustrates the ice curve correction (as described in Sect. 3.4.3).
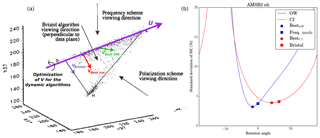
Figure 4(a) Three-dimensional diagram of open-water (H) and closed-ice (ice line between D and A) brightness temperatures in a 19V, 37V, 37H space (black dots). The original figure is from Smith (1996). The direction U (violet, sustained by unit vector u defined in Sect. 3.4.3) is shown, and vectors vBristol (blue), vBest-ice (red), and vBest-OW (green) are added, as well as an illustration of the optimization of the direction of V for the dynamic (self-optimizing) algorithms. (b) Evolution of the SIC algorithm accuracy for open-water (blue) and closed-ice (red) training samples as a function of the rotation angle θ in the range [−90∘; 90∘]. Square symbols are used for the BFM (frequency mode) and BRI (Bristol) algorithms. Disk symbols locate the new, self-optimizing algorithms.
The left-hand panel of Fig. 4 is from Smith (1996) and modified with colours to describe how BFM (frequency scheme), BPM (polarization scheme) and BRI (Bristol algorithm) view the open-water (scatter around H) and closed-ice (scatter along the D–A line) data in the three-dimensional (19V, 37V, 37H) TB space. The view direction of BRI is equivalent to projecting the TB data on a data plane, which Smith (1996) chose to contain both the closed-ice line (D–A) and the open-water point H. Because this particular plane offers the largest dynamic range between the closed-ice and open-water signatures, Smith (1996) states that it is an optimum projection plane. This, however, fails to recognize that the scatter of the closed-ice points around the line and that of open-water TB samples around the point H are anisotropic in the (19V, 37V, 37H) TB space. The open-water scatter has increased variance along the directions resulting from weather effects (including wind speed, cloud liquid water, and water vapour) on the emissivity of water. The closed-ice scatter also has increased variance directions, e.g. due to ice-type and snow characteristics. Because of these anisotropies, the optimal projection plan will generally not be that of BRI.
Our new algorithm is a generalization of BRI. Its principle is also introduced in Fig. 4 (left panel). Like in BRI we seek an optimum “data plane” on which to project the TB data, and we impose that this plane holds the closed-ice line (the D–A line, supported by unit vector u). Vector u is computed by principal component analysis (PCA) and is the direction with highest variance in the CI TB samples. Conversely to BRI, we do not impose H on the projection plane. We rather rotate the plane around u and seek the optimum rotation angle θ that yields best SIC accuracy. On Fig. 4 (left panel), we mark three unit vectors v, corresponding to three different rotation angles and thus projection planes. By convention, θ=0∘ defines the BFM (19V, 37V) plane, and ∘ defines the BPM (37V, 37H) plane. The BRI plane typical has values around ∘. By varying θ the optimization process samples several planes and eventually returns the optimal angles θOW and θCI that respectively define the BOW and BCI algorithms. This optimization step allows us to cope with the anisotropy of the OW and CI TB samples in the (19V, 37V, 37H) TB space. The right-hand panel of Fig. 4 shows the process of such an optimization in a case using AMSR2 data from the Northern Hemisphere. The solid lines plot the variation in the accuracy (measured as standard deviation of SIC, on the y axis) of the SIC algorithms defined by the rotation angle (x axis) against the OW (blue) and CI (red) training TB data. The minimum of the blue and red curves are not achieved at the same angle. This is a clear illustration that there cannot be a single SIC algorithm that performs best both on low-concentration and high-concentration conditions and confirms the strategy already adopted by Comiso (1986), Andersen et al. (2007), and Tonboe et al. (2016) to construct hybrid algorithms.
Figure 4 (right panel) also shows that the optimum rotation angle for OW cases is generally not exactly at θ=0∘ (BFM). Likewise, the optimum rotation angle for CI cases is generally not the same as that corresponding to the BRI plane. θOW (blue disc) and θCI (red disc) thus indeed define more accurate algorithms than BFM and BRI. In that particular example, the improvement is mostly for OW conditions and limited for CI conditions. The values of θOW and θCI will vary with the exact frequencies, calibration, or viewing angle of the instrument (Table 2), as well as with the OW and CI signatures that exhibit regional, seasonal, and interannual variations. The new hybrid, self-optimizing algorithms described in this section can always be tuned to available training data (see Sect. 3.3) and deliver optimum and time-consistent performance.
We can draw some additional information from the right-hand panel of Fig. 4. First, we seem to confirm the findings of Smith (1996) that BRI performs better than BPM (that corresponds to ∘). Indeed, the red curve increases all the way to ∘ and shows poor algorithm accuracy for the (37V, 37H) projection plane. Second, we observe that both the blue and red curves hit a maximum standard deviation (minimum accuracy) somewhere around ∘ (the peak value is outside the y range of the plot). This quite simply corresponds to the worst possible choice of projection plane, for which the OW TB data are projected onto the CI ice line, resulting in the smallest dynamic range between OW and CI signatures.
The geometric descriptions above were all carried out in a (19V, 37V, 37H) space. The same reasoning can, however, be carried within other 3-D TB spaces, as long as such spaces offer a clustering of the CI conditions along an ice line and sufficient dynamic range between the OW signature and the CI line. In the new CDRs, we use two different TB spaces: the OSI-450 and SICCI-25km CDRs use the (19V, 37V, 37H) space, while the SICCI-50km CDR uses the (6V, 37V, 37H) space. Both TB spaces feature two higher-frequency channels with same wavelength but alternate polarization (37 GHz in both cases), and a lower-frequency vertically polarized channel (19V or 6V). The role of the higher frequencies is to ensure a significant spread of the CI TB samples along the ice line and thus offer a good base for computing vector u with PCA. They also bring a higher spatial resolution to the retrieved SIC, since higher-frequency channels achieve higher spatial resolution (Table 2). The role of the lower vertically polarized channel is to ensure a sufficient dynamic range between OW and CI signatures and thus aim to reduce retrieval noise. This is at the cost of bringing a coarser spatial resolution into the algorithm.
This section has so far covered how the new algorithms are designed and tuned to training data. At the end of the tuning process, the unit vector u defining the closed-ice line, the two angles θOW and θCI, and the TB coordinates of the OW and CI mean tie points are recorded and stored to disk for later use. These values are the tuned parameters needed to apply the algorithms. Applying the algorithm to a set of new TB data (e.g. a new swath of instrument data) is then straightforward. Each TB triplet – (19V, 37V, 37H) or (6V, 37V, 37H) – is projected onto the two optimal planes (defined by u and each of the θ angles), and a BFM-like geometric SIC algorithm is applied in both planes (like in Fig. 3 but the x axis and y axis are now along directions in the projection plane), yielding two values: SICBOW and SICBCI. The two SIC values are combined using Eq. (1) to yield the final SIC estimate.
3.3 Dynamical tuning of the SIC algorithm
As described in the previous section, tuning the algorithms requires two sets of training data: one from OW areas (SIC = 0 %) and one from areas we assume have fully CI cover (SIC = 100 %). As in Tonboe et al. (2016), the training of the algorithms is performed separately for each instrument and for each hemisphere. In addition, the training is updated for every day of the data record and is based on a [−7; +7 days] sliding window worth of daily samples (where Tonboe et al., 2016 used a [−15; +15 days] sliding window). Our sliding window is made shorter so that tie points react more rapidly to seasonal cycles, e.g. onset of melting.
The dynamic training of our algorithms allows us to (a) adapt to interseasonal and interannual variations of the sea-ice and open-water emissivity, (b) cope with different calibration of different instruments in a series, or between different FCDRs, (c) cope with slightly different frequencies between different instruments (e.g. SMMR, SSM/I, and AMSR-E all have a different frequency around 19 and 37 GHz; see Table 2), (d) mitigate sensor drift (if not already mitigated in the FCDR), (e) compensate for trends potentially arising from the use of NWP reanalysed data to correct the TB (see Sect. 3.4.1).
As in Tonboe et al. (2016), the CI training sample is based on the results of the NASA Team (NT) algorithm (Cavalieri et al., 1984): locations for which the NT value is greater than 95 % are used as a representation of 100 % ice (Kwok, 2002). Recent investigations, e.g. during the ESA CCI Sea Ice projects, confirmed that NT was an acceptable choice for the purpose of selecting closed-ice samples. The tie points for applying the NT algorithm to SMMR, SSM/I, and SSMIS are taken from Appendix A in Ivanova et al. (2015). The same tie points are used for AMSR2 (not covered by Ivanova et al., 2015) as for AMSR-E. To ensure temporal consistency between the SMMR and later instruments, the closed-ice samples for NH are only used for algorithm tuning if their latitude is less than 84∘ N, which is the limit of the SMMR polar observation hole (Table 2).
The selection of the OW tie-point samples has been revised since Tonboe et al. (2016), which used fixed ocean areas at middle to high latitudes. The training areas now vary on a monthly basis, and follow the sea-ice cover more closely. In practice, the OW locations are those falling in a 150 km wide belt just outside the monthly varying maximum ice extent climatology (which is itself described in Sect. 3.6).
3.4 Strategies to further reduce systematic errors and random noise
The algorithms described in Sect. 3.2 are self-optimizing so that they yield the highest accuracy at high- and low-concentration ranges. Nevertheless, all TB triplets with a departure from the mean CI or OW signatures will yield a departure from 0 % and 100 % sea-ice concentration. Random departures that do not have apparent spatial or temporal structures are often referred to as “random noise”, while departures that are somewhat stable (correlated) in space and time are referred to as “systematic errors”. Analysis of time series of sea-ice concentration maps retrieved from the algorithm from Sect. 3.2 reveal that the departure at low-concentration range (open water) is typically random noise, while more systematic errors are observed at high-concentration range (closed ice). This is explained by the different nature of the error sources playing a role at these two ends of the sea-ice concentration range: weather-related effects at synoptic scales over open water, and surface emissivity variability (due to ice type, temperature of the emission layer, snow depth, etc.) over closed ice. In this section, we describe strategies implemented in the processing chain to further reduce random noise over open water, and systematic errors over closed ice. Both correction steps are applied during the second iteration of the L2 chain (Fig. 2) and we note SICucorr (uncorrected), the uncorrected SIC value, before the start of the second iteration.
3.4.1 Radiative transfer modelling for correcting atmosphere influence on brightness temperatures
As described in Andersen et al. (2006) and confirmed in Ivanova et al. (2015), the accuracy of retrieved sea-ice concentration can be greatly improved when the brightness temperatures are corrected for atmospheric contribution by using a radiative transfer model (RTM) combined with surface and atmosphere fields from NWP reanalyses. The correction using NWP data is only possible in combination with a dynamical tuning of the tie points, so that trends from the NWP model are not introduced into the sea-ice concentration data set. The correction scheme implemented in the new CDRs is based on a double-difference scheme, similar (but not identical) to that described in Andersen et al. (2006) or Tonboe et al. (2016).
The scheme evaluates the correction offsets δTB (one per channel), the difference between two runs of the RTM: TBnwp uses estimates from NWP fields (in our case ERA-Interim), while TBref uses a reference atmospheric state with the same air temperature as TBnwp, but zero wind, zero water vapour, and zero cloud liquid water. δTB is thus an estimate of the atmospheric contribution at the time and location of the observation.
For TBnwp, the RTM function F simulates the brightness temperature emitted at view angle θ0 by a partially ice-covered scene with sea-ice concentration SIC, and with surface and atmospheric states described by Wnwp (10 m wind speed, m s−1), Vnwp (total columnar water vapour, mm), Lnwp (total columnar liquid water content, mm), and TS (2 m air temperature). θinstr is the nominal incidence angle of the instrument series (see Table 2). Our double-difference scheme is thus both a correction for the atmosphere influence on the TB (as predicted by the NWP fields) and a correction to a nominal incidence angle. The latter is required to stabilize the DMSP SSM/I F10 signal, the view angle of which varied significantly: the peak-to-peak daily average incidence angle variation due to the platform's orbital drift was 52.6–53.7∘ according to Colton and Poe (1999). The typical values of δTB range from about 10 K over open water to few tenths of a kelvin over consolidated sea-ice. The liquid water content (L) fields from global NWP fields (and ERA-Interim in particular) were found to not be accurate enough to be used in our atmospheric correction scheme (Lu et al., 2018). The TB are thus not corrected for L (L=0 in both TBnwp and TBref), and the induced remaining noise transfers into uncertainty in SIC.
We use the remote sensing systems (RSSs) RTM, for which the tuning to different instruments is documented in Wentz (1983) for SMMR, Wentz (1997) for SSM/I and SSMIS, and Wentz and Meissner (2000) for AMSR-E and AMSR2. It is a parameterized, fast RTM optimized for the frequencies and view angles covered by the passive microwave sensors at hand. It originally allowed ocean and atmosphere simulations and was later extended to cover sea-ice surface conditions (Andersen et al., 2006). Since the RTM is used in the double-difference scheme described above, accurate calibration of the RTM simulation with the measured brightness temperatures is not critical since such offsets cancel out. The atmospheric correction step has more impact over open-water and low-concentration values than over closed-ice conditions. This is because of (1) a generally drier atmosphere above the consolidated ice pack, (2) the effect of wind speed on ocean (and not sea-ice) emissivity, and (3) the low emissivity and high reflectivity of water at the frequencies we use in SIC algorithms (Andersen et al., 2006).
3.4.2 Open-water filtering
The weather filters (WFs) of Cavalieri et al. (1992) have been used in basically all available SIC CDRs except the earlier EUMETSAT OSI SAF data sets (Andersen et al., 2007; Tonboe et al., 2016). WFs are algorithms that combine TB channels to detect when rather large SIC values (sometimes up to 50 % SIC) are in fact noise due to atmospheric influence (mainly wind, water vapour, cloud liquid water effects) and should be reported as open water (SIC = 0 %). The concept of WFs is very different from the atmospheric correction of TB described in the previous section: the atmospheric correction reduces noise in the resulting SIC fields (but does not yield exactly SIC = 0 % over open water), while the WF is a binary test that decides whether a pixel should be set to exactly SIC = 0 % or left unaffected. In the new CDRs, we combine both approaches as we apply the WFs after the atmospheric correction.
While WFs are effective at removing false sea ice in open-water regions, they will always falsely remove (detect as open water) some amount of low-concentration (and/or thin) sea ice, especially along the ice edge (Ivanova et al., 2015). This is why the OSI SAF SIC CDRs have so far not adopted WFs and why the effect of WFs can be fully reverted in our new SIC CDRs on an ad-hoc basis by using status flags in the product files (see Sect. 4.1).
The WF by Cavalieri et al. (1992) detects (and consequently forces SIC to 0 %) all observations with either GR3719v > 0.050 and/or GR2219v > 0.045 as open water. The GR notation stands for gradient ratio and this quantity is computed, e.g. as GR3719v = (). Many investigators have re-used these thresholds unchanged, while they should really be adapted to the different wavelengths and calibration of the different instruments. For example, Spreen et al. (2008) adapted the GR3719v threshold to 0.045 and GR2219v to 0.040 when processing sea-ice concentration with AMSR-E data. The NOAA/NSIDC sea ice concentration CDR uses the Cavalieri et al. (1992) thresholds, with the exception of Southern Hemisphere processing for SSMIS F17, where the GR3719v threshold is set to 0.053 (Algorithm Theoretical Basis Document for Meier et al., 2017).
Following Lu et al. (2018), we use a WF computed from TB that has been corrected for atmospheric influence and features a test for GR3719v only. There are two reasons for not using GR2219v: (1) a near 22 GHz channel is not available throughout the satellite time series (Sect. 2.1); and (2) the correction of water vapour using ERA-Interim data is effective enough in polar regions so that very limited additional screening is triggered by GR2219v when applied after TB correction. Indeed, GR2219v is mostly effective at detecting water vapour effects, while GR3719v is effective at screening cloud liquid water and wind-roughening effects (Cavalieri et al., 1995).
The functioning of the WF is illustrated in Fig. 3. In the (19V, 37V) diagram of Fig. 3, the GR3719v =T isolines are steeper than the consolidated ice line (A–D). For selected values of T, the isoline intersects the regions of typical open-water and low-concentration ice (the solid blue isoline GR3719v = 0.058 is plotted as an illustration). All TB data falling below the GR3719v isoline will result in GR3719v > T and will thus be flagged as OW (SIC = 0 %) by the GR3719v test. Most of the OW TB data (grey triangle symbols) are thus flagged as OW, as expected. Some low-concentration TB data (not shown, but falling between H and (A–D), closer to H) will also be detected as OW by the GR3719v test. This is an illustration of how WFs based on this gradient ratio will not only successfully detect false sea ice as open water, but also wrongly result in ice-free conditions where some true sea ice should have been observed. The greediness of the GR3719v filter is controlled by the threshold T, the tuning of which is of paramount importance for the temporal consistency of the climate data record. The varying signature of sea-ice and ocean emissivity with time and hemisphere, the different frequencies of the 19 and 37 GHz channels for different instruments, and the varying effects of atmospheric correction all prevent the adoption of fixed thresholds. Instead, we adopt a dynamic approach to tune the threshold. Our WF is tuned to avoid removing true ice with concentration larger than 10 %, on average. The tuning is shown in Fig. 3. First, the coordinates for the point J are computed: J falls where the SIC = 10 % isoline (thick blue line) crosses the (blue, dotted) line between the OW signature point H and a point at the rightmost end of the line A–D. Then, the GR3719v value corresponding to J is computed and used as a threshold T. Since the exact locations of H, A, and D vary for each instrument, hemisphere, and day in the data record, our threshold T will change (although slightly) during the whole data record, without the need for prescribed values (such as T=0.05 for the Cavalieri, 1992 WF). The value of 10 % SIC is chosen to be below the threshold commonly used for defining the sea-ice extent (15 % SIC) to ensure that the weather filter does not interfere when computing the sea-ice extent.
We note finally that the name “weather filter” can be misleading as the non-expert could understand that it is meant for filtering out weather effects (false sea ice) from calm open-water and low-ice-concentration conditions. As seen in Fig. 3, this is not how the GR3719v filter works, as it will remove true sea ice as well, even in calm weather conditions (OW samples below J). In addition, GR3719v contains information on sea-ice type (Cavalieri et al., 1984) and it is desirable that the filter should work equally for first-year and multi-year sea ice. For these reasons, we refer to such a filter as an “open-water filter” (OWF) and include a test for the SIC value. The OWF implemented in the new CDRs is thus defined by the following two tests (corresponding to the thick solid blue line in Fig. 3):
Notably, we compute OWFs in swath projection, in the Level 2 chain (Fig. 2). As a result, each FoV observation at Level 2 is attached to a binary flag corresponding to OWF detection. This binary flag is combined during gridding and daily averaging to yield Level 3 fields of OWFs. This is a better approach than computing WFs from daily averaged gridded TB data, which will smooth and smear the sea-ice edge region, as well as rapidly changing weather effects such as cloud liquid water content or wind roughening. Computing OWFs at Level 2 can also help to mitigate the potential impacts of changes in satellite crossing time between different missions. The impact of the dynamic tuning of the OWF is evaluated in Sect. 4.2.1.
3.4.3 Reducing systematic errors at high-concentration range
Wintertime, monthly averaged maps of SICucorr exhibit systematic errors at high-concentration ranges, which are especially visible in the central Arctic Ocean. A novel correction scheme is implemented as part of the second algorithm iteration (Fig. 2) that effectively mitigates most of these systematic errors over the basin.
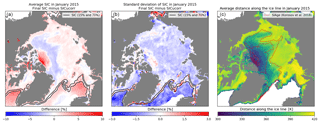
Figure 5(a, b) Difference maps between the January 2015 mean (a) and temporal variability (b) of the final SIC and the uncorrected SIC (SICucorr) in the Arctic Ocean. Black solid lines are at the 15 % and 70 % SIC levels (marginal ice zone). (c) January 2015 mean distance along the ice line (DAL) values, red lines are transitions between first-year sea ice, second-year sea ice, and older sea ice from Korosov et al. (2018).
By construction, SIC algorithms BFM, BPM, BRI, and our new dynamic algorithms consider that the SIC is exactly 100 % when the input TB falls on the consolidated ice line (Fig. 3). The concept of an ice line has sustained the development of SIC algorithms for decades, since it allows algorithms to return SICs close to 100 % for all consolidated ice conditions, whatever the type of sea ice (multi-year ice, first-year ice, mixture of types). However, careful analysis of the spread of consolidated ice samples along the ice line reveals that systematic deviations exist and are stable with time. These systematic deviations draw a consolidated sea-ice curve, as illustrated with the solid black curve around the 100 % SIC samples. These deviations are best shown in a coordinate system in which abscissae are computed as u.T (dot product of u the unit vector sustaining the consolidated ice line, and T a 3-D TB triplet in TCI, Fig. 4) and the ordinate as BCI(T) (the result of the best ice SIC algorithm for a given TB triplet). We refer to the quantity u.T as the distance along the ice line (DAL). Since u points from multi-year ice to first-year sea ice (Sect. 3.2, and Fig. 4), older ice have lower DAL values than younger ice. In winter Arctic conditions, it is typical to observe that BCI(T) values are consistently lower than 100 % (down to 85 %–90 %) for old ice (low values of DAL) and consistently higher than 100 % (up to 105 %–110 %) for new and first-year ice (high values of DAL). In between these two extremes, the BCI(T) values oscillate between being below and over the SIC = 100 % line. Our novel correction scheme moves the concept of an ice line to an ice curve that more closely follows the BCI(T) samples along the u axis. A new ice curve is tabulated for each day in the record by binning the BCI(T) values by their DAL values. This consolidated ice curve defines the SIC 100 % isoline during the second iteration of Level 2, and – conversely to the atmospheric correction described in Sect. 3.4.1 – has the greatest effect on consolidated ice regions. It is noteworthy that the sea-ice curve shown in Fig. 3 is for illustration purpose. As part of the processing, the consolidated ice curve is not used in the two-dimensional BFM space, but in the three-dimensional data plane of the dynamic SIC algorithm (see Sect. 3.2). The amplitude of the sea-ice curve around the sea-ice line can be different in shape in the SIC algorithm plane. In addition, the ice curve in Fig. 3 is fitted through the consolidated ice points from the ESA CCI Sea Ice RRDP (Pedersen et al., 2018) that spans several years and winter months and thus illustrates an average sea-ice curve. The consolidated sea-ice samples we extract dynamically for [−7; +7 days] sliding windows (Sect. 3.3) will typically exhibit more variability due to shorter-term changes in sea-ice signatures.
Figure 5 (left and middle panels) show the spatial distribution of the total correction for January 2015 (SIC minus SICucorr), thus including both the effect of the correction based on the consolidated ice curve and the effect of the RTM-based correction of the TB. Black solid lines show the mean sea-ice edge region (at 15 % and 70 % SIC values) during the same period. The left panel shows the average total correction (daily maps of SIC minus SICucorr averaged over the month of January 2015), while the centre panel shows the effect of the total correction on SIC variability (variability is the standard deviation of daily SICucorr maps throughout the month minus the same variability of daily SIC maps after correction).
Over closed-ice conditions (inside the 70 % SIC isoline), the regional patterns of the correction are clearly visible and seem to match variations in sea-ice age: a large positive correction (increased SIC) north of the Canadian Arctic Archipelago and Ellesmere Island (intense red colour) where the ice is oldest in the Arctic, moderate negative correction over a large part of the central basin (extending from the central Beaufort Sea, over to the North Pole, and to northern Greenland, light-blue colour, second-year ice), and a slightly positive correction again over large parts of the Siberian Arctic (light-red colour, first-year ice). The mean January 2015 DAL is shown in Fig. 5 (right) (blue, green, and yellow colours).
On Fig. 5 (right) we observe an overall increase of the DAL value from the Canadian Arctic Archipelago (multi-year ice) across the pole and towards the Laptev and Kara seas (first-year ice). To confirm the link between DAL and sea-ice age, we overlay contours ≥1 year, ≥2 years, and ≥3-year-old sea ice for January 2015 from Korosov et al. (2018) on the right panel. Korosov et al. (2018) developed an improved Lagrangian-based sea-ice age tracking algorithm using the sea-ice drift product of the EUMETSAT OSI SAF (Lavergne et al., 2010). The correspondence in the transitions of DAL values with the contour lines of sea-ice age is very good, indicating that a combination of DAL (right panel) and ice curve correction (left panel) could be used for sea-ice type (if not age) classification studies. This is outside the scope of our study, which is focused on SIC algorithms and the new data records.
Figure 5 (centre) shows the result of the ice curve correction on SIC variability. In the regions covered with sea-ice (>=70 % SIC), the shades of light blue indicate that the variability at high concentration is rather consistently reduced by about 1 %–2 % SIC by the ice curve correction: the SIC after correction is a more accurate description of a nearly 100 % ice cover. A limited number of regions show no improvement (white colour) or slight degradation. This reduction in the variability comes in addition to the correction for the systematic errors (e.g. underestimation north of Canadian Arctic Archipelago; see left panel for which the ice curve correction was designed). The analysis of the closed-ice (>=70 % SIC) region in Fig. 5 thus confirms that the ice curve correction works as expected at high-concentration range and is potentially linked to the age of sea ice.
In the open-water regions of Fig. 5 (outside the 15 % SIC contour), the reduction in variability (centre panel) is even larger (3 %–4 % SIC) than over closed-ice regions. This reduction is the result of the atmospheric correction step, described in Sect. 3.4.1. From the left panel, it appears that the atmospheric correction step on average increases SIC (shades of red) over open-water regions close to the sea-ice edge, e.g. in East Greenland Sea, Barents Sea, and in Labrador Sea. These regions generally present negative SICs before correction and are brought closer to 0 % SIC by the process of atmospheric correction. This is due to the training OW samples being selected in lower-latitude conditions (ocean surface, atmosphere conditions) rather than prevailing closer to the ice edge and is also discussed in Sect. 4.2.3 when evaluating uncertainties.
Still in Fig. 5 (centre panel), the increased variability (red tones) between the 15 % and 70 % isolines follows logically from the two above-mentioned reductions: the corrections enable more accurate retrievals of SICs; thus the ice edge is more sharply defined in the daily SIC fields, and this results in higher variability on a monthly basis.
In this section, we described the strategies we implemented to improve the accuracy of the SIC algorithms. In the next section, we discuss how the remaining noise is quantified and reported to the users of the data records in the form of uncertainties.
3.5 Uncertainties
Spatially and temporally varying uncertainty estimates for each and every SIC value are required of state-of-the-art CDRs (GCOS-IP, 2016). Uncertainties are needed as soon as the data are compared to other sources (e.g. other similar data records) or when data are assimilated into numerical models. However, there is no unique way to derive nor to present uncertainties in EO data (Merchant et al., 2017).
The approach to derive and present uncertainties in the new SIC CDRs is mostly similar to that of Tonboe et al. (2016): we make the assumption that the total uncertainty σtot is given by two uncertainty components. That is,
where σalgo is the inherent uncertainty of the SIC algorithm (algorithm uncertainty) including sensor noise and the residual geophysical noise quantified as variability around the OW and CI mean signatures, and σsmear is the representativeness uncertainty due to resampling from satellite swath to a grid (smearing uncertainty) and the mismatch between footprints at different channels.
The derivation of σalgo is to a large extent similar to that described in Tonboe et al. (2016). This term is derived from the accuracy (estimated as statistical variance) of the algorithm for retrieving 0 % (100 %) when applied onto the OW (CI) training data samples (Sect. 3.3). This uncertainty term is computed at Level 2 (Fig. 2). Each Level 2 SIC estimate in the data record has an associated σalgo value.
The uncertainty term σsmear is a representativeness uncertainty. It measures the increase in uncertainty due to mismatching spatial dimensions such as when (a) the satellite sensor footprint potentially covers a larger area than that of a target grid cell, or when (b) the imaging channels used by the SIC algorithms do not have the same FoV diameter. Table 2 lists the dimensions relevant for discussion of these two effects. Effect (a) is that the size of the footprint of the 19 GHz channels of the SMMR, SSM/I, and SSMIS instruments is larger than the resolution of the grid used to present the SIC field (25×25 km; see Table 1). Effect (b) is that the footprint of the 37 GHz channels is smaller than that of the 19 GHz ones, so that the two frequencies entering the SIC algorithms do not cover the same area of the Earth's surface. Intuitively, both effects should have no or limited impact where the sea-ice cover is homogeneous (fully consolidated sea ice or open water). It should be at a maximum where sharp spatial gradients occur, typically at the sea-ice edge. The smearing contribution σsmear is difficult to derive analytically and we carry on the approach of Tonboe et al. (2016) to parameterize σsmear as a function of a proxy. For the three new CDRs we parameterize σsmear as a function of the ( value, that is the difference between the highest and lowest SIC values in a 3×3 grid cell neighbourhood around each location in the grid. Specifically,
where K is a scalar with a value that depends on the FoV diameter of the instrument channels used for the SIC computation and the spatial spacing of the target grid. Several other proxies for the local variability of the SIC field (among others the 3×3 standard deviation, the Laplacian, and power-to-mean-ratio) were tested and this one was selected for its simplicity and robustness. Values of K were tuned using a footprint simulator and selected cloud-free scenes of the marginal ice zone imaged by the Moderate-Resolution Imaging Spectroradiometer (MODIS) as described in Tonboe et al. (2016). The MODIS images are first classified as water and ice at full resolution. Two sets of coarser-resolution SIC fields are then prepared: (1) the footprint simulator is applied to prepare a synthetic sea-ice concentration field at the resolution of the frequency channels, and (2) the high-resolution classified pixels are binned into regular grid cells, e.g. at the target resolution of the CDR (e.g. 25×25 km). The mismatch between the two fields is what we call the smearing uncertainty and is parameterized against proxies such as (MAX−MIN)3×3. A value of K=1 was found to yield good results for all three CDRs. The value for σsmear is computed as part of the Level 3 chain (Fig. 2), after gridding and daily averaging. The total uncertainty σtot is finally computed using Eq. (4). In the data files, the total, the algorithm, and the smearing uncertainty fields are made available.
3.6 Other relevant algorithms and processing steps
This section introduces some other algorithms and processing steps that are important to the generation of the data records, but are either less critical for prospective users of the data or have undergone little evolution since Tonboe et al. (2016).
Due to the coarse resolution of the sensors used, especially SMMR, SSM/I, and SSMIS (Table 2), the TB data are influenced by land emissivity several tens of kilometres away from the coastline. The emissivity of land is comparable to sea-ice emissivity and much higher than water emissivity. This means that sea-ice concentration will be consistently overestimated in coastal regions. In Tonboe et al. (2016), a statistical method similar to Cavalieri et al. (1999) was implemented as post-processing to the daily-gridded sea-ice concentration maps. Such a method showed limitations and the new SIC CDRs now introduce explicit land spillover correction of the TB at all used channels and on swath projection. The correction algorithm is described in detail in Maass and Kaleschke (2010). The basic principle is that a fine-resolution land mask is used together with the antenna viewing geometry to estimate (and correct for) the simulated contribution of land emissivity to the observed TB. The algorithm of Maass and Kaleschke (2010) was adopted with some modification and tuning, including (a) the computation of the fraction of land in each FoV in the view geometry of the antenna (not after projection to a map), (b) the approximation of the antenna pattern functions as Gaussian (normal distribution) shapes indexed on the aperture angle from the central view direction, instead of distance on a projection plane. At the end of this step, TB of FoV that overlap land and ocean are corrected for the contribution by land and can enter the Level 2 sea-ice concentration algorithms. Note that, although this swath-based correction step is quite efficient at reducing land spillover contamination, a statistical method similar to that of Cavalieri et al. (1999) still had to be applied at Level 3; this is further discussed in Sect. 5.2.
The land masks and climatology for the new SIC CDRs have been revised since Tonboe et al. (2016). New land masks for the target 25×25 km grids (one for NH and one for SH) were computed based on the Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) 0.05×0.05∘ land mask (Donlon et al., 2012). This mask was re-used in the ESA CCI sea surface temperature (SST) L4 data records and was selected as the input mask for the new SIC CDRs to increase cross-ECV consistency. The masks are tuned to closely match that of the NSIDC SIC CDR (the NSIDC “SSM/I” 25 km Polar Stereographic mask). On average, in the NH, this corresponds to setting all 25×25 km grid cells with a fraction of land lower than 30 % to water (and these cells can thus potentially be covered with sea ice). There is no right or wrong binary land mask at such coarse resolution, and the decision to tune to the NSIDC SIC CDR land mask is to help an intercomparison of data records. By the same token, the monthly varying maximum sea-ice extent climatology implemented in Meier et al. (2017) was used as a basis for our own climatology. The modifications included manual editing of some single pixels based on US National Ice Center, Canadian Ice Service, and Norwegian Ice Service ice charts (e.g. along the coast of northern Norway, for some summer months in the vicinity of Nova Scotia). The climatology of peripheral seas and large freshwater bodies (e.g. Bohai and Northern Yellow Seas, Great Lakes, Caspian Sea, and Sea of Azov) was also revisited. The cleaned climatologies were then expanded with a buffer zone of 150 km in the NH and 250 km in the SH. The larger expansion in SH is to cope with the positive trends in the SH sea-ice extent (Hobbs et al., 2016). The expanded monthly sea-ice climatology is used both to mask the final product and for defining the monthly varying area where the open-water training samples were selected (Sect. 3.3).
As described in the sections above, all the geophysical processing is performed on swath projection (Level 2 processing). Gridding (using Gaussian weighting of distance) and daily averaging (equal weights) of the swath data are tackled as an initial step of the Level 3 chain (Fig. 2). The methodology is mostly similar to that of Tonboe et al. (2016) as swath data from all available instruments of similar spatial resolution are combined into daily maps of the NH and SH polar regions. It is noteworthy that full advantage of the overlap of satellite missions (see Fig. 1 and Table 2) was taken in order to reduce the occurrence of missing data areas as much as possible in the daily composited fields. This contrasts with the SIC CDR method of Meier et al. (2017), which uses one SSM/I or SSMIS sensor at a time.
Despite using all the sensors, some data gaps still appear in the daily SIC maps, especially in the early part of the data record (late 1970s to mid-1990s). These data gaps are filled by interpolation (both spatially and temporally) to yield a more user-friendly data record. The polar observation gap (largest for SMMR and SSM/I; see Table 2) is filled by interpolation as well. All interpolation of missing data is performed with basic isotropic schemes using Gaussian weighting in the space domain, and equal weighting in temporal domain. No model data or advanced methods (among others Strong and Golden, 2016) were implemented. All interpolated data are clearly marked in the product files using status flags. Days with fully missing input data (e.g. every other day in the SMMR period) are not created by interpolation, and the files are missing.
4.1 The data records and selected examples
The SIC CDR released by the EUMETSAT OSI SAF (OSI-450) extends from January 1979 through to December 2015. It uses data from SMMR, all SSM/I (F08, F10, F11, F13, F14, F15), and three SSMIS (F16, F17, and F18). It is delivered on two Equal Area Scalable Earth 2 (EASE2) grids with 25×25 km spacing (Brodzik et al., 2012, 2014), one for the Northern Hemisphere and one for the Southern Hemisphere. SMMR data for the period October to December 1978 are not included in the CDR because of the unavailability of ERA-Interim data for a correction of the atmospheric influence on TB (Sect. 2.2). OSI-450 has the following digital object identifier (DOI): https://doi.org/10.15770/EUM_SAF_OSI_0008. Data are freely available to any users from the EUMETSAT OSI SAF web pages (http://www.osi-saf.org/, last access: 15 June 2018).
The two SIC CDRs released by the ESA CCI Sea Ice project (SICCI-25km and SICCI-50km) extend over two disjointed periods and process data from AMSR-E (June 2002 to October 2011) and AMSR2 (July 2012 to May 2017). SICCI-25km (DOI: https://doi.org/10.5285/f17f146a31b14dfd960cde0874236ee 5) is delivered on the same EASE2 25×25 km grids as the OSI SAF CDR. SICCI-50km (DOI: https://doi.org/10.5285/5f75fcb0c58740d99b07953797bc04 1e) is delivered on an EASE2 50×50 km grid, with cells that cover exactly four 25×25 km cells of the SICCI-25km and OSI-450 grids. Both SICCI-25km and SICCI-50km are freely available to any user from the ESA CCI Data Portal (http://cci.esa.int/data/, last access: 15 June 2018). Figure 6 shows the OSI-450 (top-left panel), SICCI-25km (top right), and SICCI-50km (bottom left) SIC fields over the Weddell Sea region on 25 September 2015. The two SIC fields on the top row are rather similar except in the marginal ice zone, where the higher resolution of the AMSR2 instrument (SICCI-25km) with respect to that of the SSMIS (OSI-450) leads to resolving finer details. The SICCI-50km SIC has increased granularity due to the lower resolution of the 6 GHz channels compared to the 19 GHz channels.
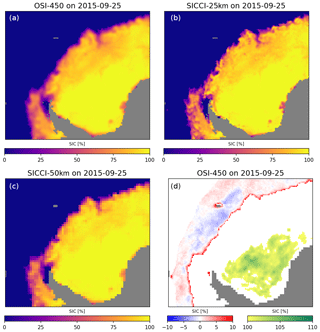
Figure 6Example SIC fields on 25 September 2015 from the three CDRs (a: OSI-450, b: SICCI-25km, c: SICCI-50km) over the Weddell Sea. Panel (d) shows the content of variable raw_ice_conc_values from the OSI-450 file for the same date and area. Note the two discontinuous colour scales for (d).
All three data records share the same data format, which is Network Common Data Format (NetCDF) version 4 (classic format). Files abide by the Climate and Forecast (CF) convention (CF-1.6) and the Attribute Convention for Data Discovery (ACDD-1.3). The variables inside the files enable a flexible use of the data. The main variable is named ice_conc and holds a SIC field where all the filters (among others the open-water filter, Sect. 3.4.2) and correction steps (among others the statistical coastal correction scheme, Sect. 3.6) are applied. This is the entry point for most prospective users of these new SIC CDRs and is the variable plotted in the top row and bottom-left panel of Fig. 6. In addition, a variable named raw_ice_conc_values gives access to the original (raw) values of sea-ice concentration before filtering is applied.
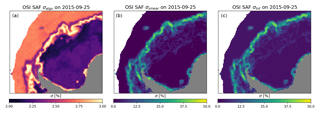
Figure 7Example fields of uncertainties on 25 September 2015 from the EUMETSAT OSI SAF CDR over the Weddell Sea. The component σalgo (a), σsmear (b), and the total uncertainty σtot (c) are shown. σtot is dominated by the σsmear contribution.
The bottom-right panel in Fig. 6 shows the content of variable raw_ice_conc_values that holds values as nominally returned by the SIC algorithm of the OSI-450 CDR on the same date and location as the three other panels. A blue–red colour scale is used for the low-range of SIC values. Both negative (blue) and positive (red) values appear that correspond to the intrinsic retrieval noise level of the SIC algorithm before the OWF is applied. All these values are indeed set to exactly 0 % by the OWF in variable ice_conc. Note how the belt of low SIC values is bordered by a dark-red region. This is very probably true low-concentration or thin sea ice that is removed by the OWF at the marginal ice zone. Removal of true sea ice by the OWF was discussed in Sect. 3.4.2. Still on the bottom-right panel, a yellow–green colour scale is used to plot large off-range SIC >100 % values. These raw values are non-physical (like the blue-shaded SIC <0 % values) and are set to exactly 100 % in variable ice_conc. They might be interesting for advanced users interested in accessing the full probability distribution function (PDF) of retrieved SIC values, for example for data assimilation (DA) applications. The off-range SIC values are also needed to compute temporal averages (e.g. monthly means) to avoid introducing biases if only SIC >=0 % or SIC =<100 % values enter the averaging. In each file, a status_flag variable indicates which flags (OWF, maximum extent climatology, etc.) or corrective steps (land spillover correction) were applied in each grid cell.
Example fields of uncertainties from the OSI-450 CDR are shown in Fig. 7. The two uncertainty components σalgo (left panel) and the smearing uncertainty σsmear (centre) are shown, as well as the total uncertainty σtot (right). The algorithm uncertainty is typically between 2 % and 3 % SIC. It is lower for sea ice than for open water because the global variability of closed sea ice is lower than the SIC variability over open water. It is noted that this variability is not due to real SIC variability but rather to ice and open-water signature variability reflected in the estimated SIC; thus it is an uncertainty. The smearing uncertainty is largest, up to 40 % SIC, at the ice edge and low, near 0 % SIC, in areas where all contributing satellite footprints cover the same SIC (e.g. open water). The total uncertainty, which is the sum (in variance) of σalgo and σsmear (Sect. 3.5), is dominated by σsmear. The patterns seen in Fig. 7 are representative of the uncertainties of all three CDRs for both hemispheres during winter. During summer, σalgo is larger by a few percent, and the increased variability inside the ice pack yields higher σsmear, leading to larger σtot.
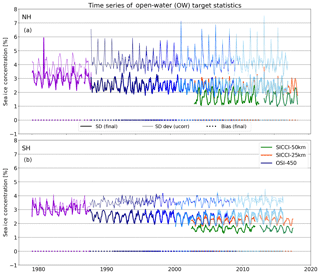
Figure 8Time series of performance statistics for the three CDRs (blue: OSI-450, red: SICCI-25km, green: SICCI-50km) over the open-water target for the Northern Hemisphere (a) and Southern Hemisphere (b). For OSI-450 and SICCI-25km, the colour of the lines is for individual satellites, as used in Fig. 1. For OSI-450, the thick (thin) solid lines plot the OW standard deviation of SIC (SICucorr). The thin solid lines are only plotted for OSI-450 so as not to clutter the plot area. The bias of SIC is plotted with a dotted line.
4.2 Evaluation results
The evaluation of a CDR needs to cover three aspects. The first is to demonstrate consistency of the methods used to derive the CDR. Key elements of our new suite of algorithms are (i) their application to different sensors (various SSM/I, AMSR-E, and AMSR2), (ii) a self-optimizing algorithm which dynamically tunes tie points to minimize SIC errors at 0 % and 100 %, and (iii) a dynamic open-water filtering (OWF) to mitigate spurious SIC values caused by residual weather influences while keeping actual low SIC. For the three SIC CDRs published here we investigate time-series plots of the optimized skills of the SIC algorithms and the temporal stability of the OWF (Sect. 4.2.1). The second aspect is to evaluate the SIC CDRs with independent SIC values. In the present paper we focus on an evaluation at 0 % and 100 % SIC; results of the evaluation at intermediate SIC with various independent SIC will be published elsewhere. The methodology used and the results are given in Sect. 4.2.2. The third aspect is to evaluate the uncertainty estimates provided with the SIC CDRs. The uncertainties should provide the range within which the SIC CDRs values are allowed to vary around the true value, and this is evaluated at 0 % and 100 % SIC in Sect. 4.2.3.
4.2.1 Monitoring stability and internal consistency
Many time-series plots can be produced to illustrate the stability and internal consistency of the three CDRs. As an example, Fig. 8 shows the time series of the algorithm training statistics at the open-water target. As described in Sect. 3.2 and 3.3, the algorithms implemented in the three CDRs dynamically tune their parameters to yield zero bias and minimum standard deviation of the computed SICs (a.k.a. best accuracy) over the open-water (OW) and closed-ice (CI) training targets. Figure 8 shows the Northern Hemisphere (NH, top) and Southern Hemisphere (SH, bottom) temporal evolution of the standard deviation (solid lines) and bias (dotted lines) of the SIC algorithms over OW target areas. Prior to further describing Fig. 8, it is important to note that the biases and standard deviations discussed here are internal to the processing chains, not an evaluation of the CDRs against independent observations of SICs. An evaluation of the CDRs against independent ground-truth observations is the topic of Sect. 4.2.2.
From Fig. 8, it is easy to see that the algorithms implemented in the three CDRs achieve zero bias (dotted lines along the y=0 axis) for all instruments and both hemispheres on a daily basis. Achieving zero bias despite the changes in central wavelengths and calibrations from one satellite to the next is one of the key advantages of using dynamically tuned algorithms (Sect. 3.3).
The impact of the explicit correction of brightness temperature for atmospheric noise effects is also clearly visible in Fig. 8, since the standard deviations resulting from uncorrected TB data (thin solid lines) are consistently above those for corrected data (thick solid lines) by about 3 % to 4 % on average, depending on the season and hemisphere. The seasonal variability is also larger from the uncorrected data, especially in the NH. It is noteworthy that the atmospheric noise reduction step does not much improve the OW standard deviation in the SH at the beginning of the OSI-450 period for the SMMR instrument (1979–1987). As noted at the end of Sect. 3.4.1, OSI-450 uses the Wentz (1983) RTM for SMMR, and the Wentz (1997) RTM for SSM/I and SSMIS. The parameterizations implemented in the SMMR RTM are probably less developed than in the SSM/I and SSMIS RTM, which might explain why the impact on our standard deviation is more limited for SMMR. Another plausible explanation is that the reanalysed fields for wind speed and water vapour from ERA-Interim are less accurate in the SMMR era than in the SSM/I and SSMIS era. We note that clear-sky radiances from SSM/I and SSMIS were directly assimilated in ERA-Interim over the ocean (Dee et al., 2011) but not SMMR radiances (P. Poli, personal communication, 2018). This can especially have an impact in the SH, where other sources of conventional observations are scarcer. Even if not as large as later in the time series, atmospheric correction does yield a positive impact on the accuracy of OW SICs during the SMMR era.
The SICCI-25km and SICCI-50km standard deviations are also plotted in Fig. 8 (only those after atmospheric correction so as not to clutter the plot area). SICCI-25km (red) achieves roughly the same OW standard deviation as OSI-450. Since SICCI-25km uses very similar frequency channels to those of OSI-450 (Table 1), it is not surprising that they achieve similar accuracy. The central frequency of the AMSR-E and AMSR2 channels (18.7 GHz) is slightly further away from the water vapour absorption line (∼22 GHz) than the SSM/I and SSMIS channels (19.3 GHz). This difference in frequency yields better accuracy for SICCI-25km than OSI-450 when using uncorrected TB data (not shown) but this effect is mostly cancelled after atmospheric correction (though not fully in SH, bottom panel). The same effect is observed for the standard deviations resulting from uncorrected SMMR TB data (purple thin line), which is consistent with a central frequency of 18.0 GHz (Table 2).
SICCI-50km (green) is more accurate than both SICCI-25km and OSI-450, by nearly 1 % in NH and 0.5 % in SH. This is expected from the choice of frequency channels, since SICCI-50km uses a C-band (6.9 GHz) channel, while SICCI-25km and OSI-450 use Ku-band (∼19 GHz). Three effects lead to better accuracies of SIC retrievals at low frequencies: (1) the atmosphere is more transparent, yielding better accuracy over OW; (2) the noise sources, such as sea-ice type, snow depth, and snow scattering, have less impact at low frequencies; and (3) the permittivity (and hence TB) of sea ice and water are more different, resulting in a larger dynamic range for sea-ice concentration retrievals. SICCI-50km is designed to be the most accurate of the three SIC CDRs. However, it achieves a coarser spatial resolution (50 km) due to the limited size of the AMSR-E and AMSR2 antenna. The time series in Fig. 8 illustrate that the algorithms behave as expected across instruments and are effectively tuned to achieve zero bias and a small retrieval noise for each instrument in the time series.
The role of open-water filters (OWFs) is to detect and remove weather-induced false sea ice over open water while ideally preserving the true low-concentration values (typically at the ice edge). As introduced in Sect. 3.4.2, the threshold of the OWF is tuned dynamically against the daily updated training data samples (thus by instrument and by hemisphere) to preserve true SIC values down to 10 %. A water–ice separation limit at 10 % SIC is an ambitious goal but is necessary to ensure that time series of sea ice extent (SIE, usually defined with a threshold of 15 % SIC) are not influenced by the OWF and only by the evolution of true SIC. Figure 9 shows time series of NH (solid lines) and SH (dashed lines, almost coinciding with NH lines) of the 1 % percentile value of all ice_conc values (thus after all filters including the OWF is applied) that are strictly positive and below 30 % SIC for the OSI-450 (blue), SICCI-25km (red), and SICCI-50km (green) CDRs. These are thus time series of the typical minimum detected SIC that are preserved by the OWFs. A solid horizontal line is drawn at 15 % SIC value, the threshold commonly chosen for SIE computations. The OSI-450 curves are very stable with time and increase only slightly from around 9 % SIC at the beginning of the period to around 10.5 % SIC at the end. Seasonal variations are visible especially at the beginning of the time series for NH cases, when typical winter values are around 7.5 % SIC and peak to 10 % SIC in summer. They are in any case well below the 15 % threshold throughout the data record and very little change is observed when transitioning between sensors. The seasonal cycles are limited to few tens of a percent at the end of the period (few percent at the beginning). The SICCI-25km curves are close to the OSI-450 ones, but at a slightly larger value of 11 %, with a seasonal variation range of about 2 %. The SICCI-25km curves are also well below 15 %. The SICCI-50km curves are those showing the largest variation. The average value for SICCI-50km is at about 10 %, but the seasonal variations are much larger, ranging from 5 % to 15 %. The temporal stability of the time series in Fig. 9 documents that the tuning of the OWFs at values close to 10 % SIC is successful for the two data records that rely on the 19 and 37 GHz for computing their SICs (OSI-450 and SICCI-25km) and is not as good for SICCI-50km, which uses the 6 and 37 GHz channels to compute the SIC values. Although SICCI-50km does not compute SICs from 19 and 37 GHz channels, its OWF is still based on the GR3719v threshold (Sect. 3.4.2). The mismatch in frequency and resolution between the channels used to compute the OWF and those used to compute SIC explains the larger variability in the SICCI-50km time series in Fig. 9.
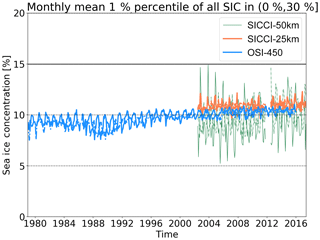
Figure 9Time series of the monthly mean 1 % percentile value of all strictly positive SICs that are below 30 % (variable ice_conc) for the three CDRs (blue: OSI-450, red: SICCI-25km, green: SICCI-50km). Solid lines are for NH; dashed lines are for SH. This time series plot investigates whether the dynamic tuning of the open-water filters results in temporal consistency of the minimum detected true SIC across all satellites.
We note in addition that both the OSI-450 and SICCI-25km CDRs dynamically tune their optimal data planes for low-concentration range θOW in the (19V, 37V, 37H) 3-D TB space, while the OWF is only tuned in the (19V, 37V) TB plane. The departure of the optimal SIC plane from the OWF plane (by convention at θ=0∘; see right-hand panel in Fig. 4) could be the cause for the slight increase of the 1 % percentile curves of OSI-450 during the time period (via an improvement of the reanalysis data entering the atmosphere correction step over time), and the different value obtained with SICCI-25km. Ideally, the OWF should be tuned in the same 3-D TB space as used for the SIC algorithms. Such 3-D-based filters do not exist at present and this is addressed as future work in Sect. 5.2. All in all, we note that all three CDRs achieve a rather stable detection of true SIC mostly below the 15 % SIC threshold commonly used to define SIE. To the best of our knowledge the temporal consistency of the minimum detected SIC has not been documented for other available CDRs, although all use OWFs.
4.2.2 Evaluation against ground truth
For the evaluation of the SIC CDRs, we used a temporal extension of the Round Robin Data Package (RRDP) by Ivanova et al. (2015) to study the strengths and weaknesses of more than 30 published SIC algorithms. Among other data sets, the RRDP v2 holds ground-truth locations for open-water cases (OW, 0 % SIC) for the period 2002–2015, as well as ground-truth locations for closed ice (CI, 100 % SIC) for the period 2007–2016. The OW locations are situated just outside the climatological mask delineating maximum sea-ice extent but well inside the buffer zone added to it in Sect. 3.6. They are distributed as evenly as possible in longitude. The CI locations are selected in areas of high sea-ice concentration and after 24 h of convergent sea-ice motion, as computed from a highly accurate SAR-based sea-ice drift product from the Copernicus Marine Environment Monitoring Service (CMEMS, http://marine.copernicus.eu, last access: 15 June 2018). The OW and CI data sets of the RRDP are described in more detail in Ivanova et al. (2015) and in Pedersen et al. (2018).
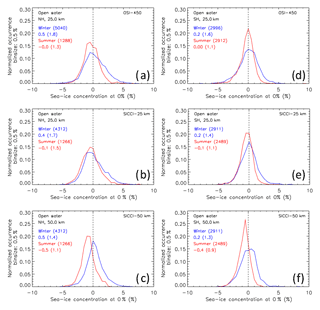
Figure 10SIC distribution around SIC = 0 % at the selected open-ocean locations for, from top to bottom, OSI-450, SICCI-25km, and SICCI-50km in the Arctic (a–c) and the Antarctic (d–f). The unfiltered distribution is shown (no OWF) by combining ice_conc and raw_ice_conc_values variables. Blue (red) curves and numbers refer to results from winter (summer); the numbers in parenthesis behind the season denote the count of cases used. Numbers below the season denote the mean SIC and 1 standard deviation (in parenthesis) in percent SIC. Bin size is 0.5 %. Distributions are normalized to give a total of 1.
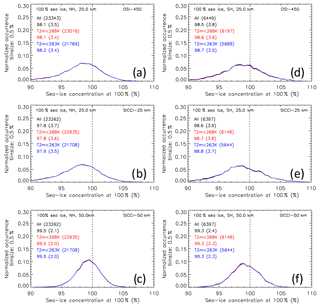
Figure 11SIC distribution around SIC = 100 % from the RRDP-2 data set for, from top to bottom, OSI-450, SICCI-25km and SICCI-50km in the Arctic (a–c) and the Antarctic (d–f). The unfiltered distribution is shown (no threshold at 100 % SIC) by combining ice_conc and raw_ice_conc_values variables. Black, red and blue curves and numbers refer to all data and data limited to ERA-Interim 2 m-air temperatures <−5 and <−10 ∘C respectively. The numbers behind the limitation text (e.g. “all”) denote the count of data used; the numbers below denote the mean SIC and 1 standard deviation (in parenthesis) in percent SIC. Bin size is 0.5 %. Distributions are normalized to give a total of 1.
For the evaluation of the SIC CDRs over open water, we extracted OSI-450, SICCI-25km, and SICCI-50km CDR SIC (variable raw_ice_conc_values) and total uncertainty σtot data at the grid cell closest to the OW locations in the RRDP v2 from 2 months in summer (August and September in the Arctic and January and February in the Antarctic) and from 3 months in winter (January to March in the Arctic and July to September in the Antarctic). For the evaluation at 100 % SIC conditions, we collocated the SIC CDRs with the SAR-based CI locations in the RRDP v2 for months November to March (Arctic) and May to September (Antarctic) in the same way as we did for open water; no spatial or temporal interpolations are performed. We note that CI ground-truth data from East Antarctica are missing completely, however, because of a lack of SAR image acquisitions. Using the status_flag variable, any SIC contaminated by land spillover effects or with high air temperatures were discarded.
For open water, we find quite similar SIC distributions around 0 % for all three CDRs for both hemispheres (Fig. 10). During winter (blue curves) OSI-450 and SICCI-25km are skewed a bit towards negative SIC in the Arctic but not in the Antarctic. During summer (red curves) we find SIC distribution to be skewed to negative SIC for all CDRs except OSI-450 in the Antarctic. Distributions are generally more narrow for SICCI-50km than for the other two CDRs. Figure 12 (a and b, black crosses) illustrates the very similar accuracies for OSI-450 and SICCI-25km with a mean SIC of 0 % or −0.2 % during summer and of ∼0.5 % during winter in both hemispheres. For SICCI-50km, the accuracy varies more than for the other two CDRs: summer is % and winter is 0.2 % to 0.5 %. The standard deviation of the mean SIC (black bars), i.e. the precision, ranges between 1 % and 2 % for all three CDRs. Without exception the precision is better (smaller standard deviation) in summer than winter. For both hemispheres, we find that the precision of OSI-450 and SICCI-25km SIC CDRs are similar to each other and poorer than for SICCI-50km, which is in line with the findings in Fig. 8.
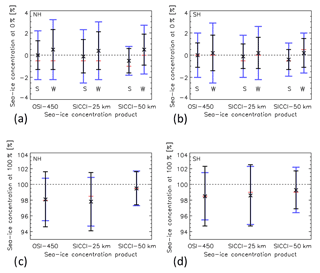
Figure 12Summary of histogram statistics from Figs. 10 and 11 for SIC = 0 % (a, b) and SIC = 100 % (c, d) for the Arctic (a, c) and the Antarctic (b, d). Crosses and black bars denote the mean SIC ± 1 standard deviation of the standard error. Red horizontal bars denote the modal SIC. Blue bars denote the range covered by the mean SIC ± 1 standard deviation of the total uncertainty. Letters S and W in (a) and (b) refer to summer and winter.
For sea ice, we find almost identical SIC distributions around 100 % for OSI-450 and SICCI-25km for both hemispheres (Fig. 11a, b, and d, e). Distributions for SICCI-50km are considerably narrower (Fig. 11c, f) and, in comparison to OSI-450 and SICCI-25km, have a modal value closer to 100 %. All three CDRs exhibit a negative bias, i.e. a modal SIC <100 %. Figure 12c, d further illustrate that SICCI-50km provides the smallest bias (best accuracy) in both hemispheres with mean SICs of 99.5 % and 99.3 % for the Arctic and Antarctic. In addition, SICCI-50km also offers the smallest SIC standard deviation of the mean (black bars), i.e. the best precision, of ∼2 % and ∼3 % for the Arctic and Antarctic. OSI-450 and SICCI-25km provide a slightly larger bias with a mean SIC of ∼98 % in the Arctic and ∼98.5 % in the Antarctic, which also comes with a higher SIC standard deviation of the mean: 3.5 % to 4.0 %.
4.2.3 Evaluation of the uncertainties
We computed the mean SIC total uncertainty σtot for OSI-450, SICCI-25km, and SICCI-50km for exactly the same set of grid cells as used in Sect. 4.2.2 (Fig. 12, blue bars).
For open water, SIC = 0 % (Fig. 12a, b), we find that mean SIC total uncertainties differ by less than 0.3 % between OSI-450 and SICCI-25km and take values of ∼2 % during summer and of ∼2.5 % during winter. For SICCI-50km, the mean SIC total uncertainty is smaller than for the other two CDRs – particularly during summer in the Northern Hemisphere, with ∼1.5 % compared to ∼2 % in winter. Without exception mean SIC total uncertainties exceed 1 standard deviation of the retrieval errors (compare black and blue bars in Fig. 12a, b). Also without exception, mean SIC total uncertainties are smaller than 2 standard deviations of the retrieval errors (not shown).
For sea ice, SIC = 100 % (Fig. 12c, d), we find that mean SIC total uncertainties for OSI-450 (∼3 %) are smaller than those for SICCI-25km (∼3.5 %) in both hemispheres. For SICCI-50km mean SIC total uncertainties are smaller than for the other two CDRs – particularly in the Northern Hemisphere, at ∼2 % (Fig. 12c). For OSI-450 and SICCI-25km, mean SIC total uncertainties are smaller than 1 standard deviation of the retrieval errors. For SICCI-50km, mean SIC total uncertainties are comparable to (Fig. 12c) or larger than (Fig. 12d) 1 standard deviation of the retrieval errors. These results are in agreement with those introduced in Sect. 4.2.1 and are mainly explained by the frequency channels used in the three CDRs: 18.7 GHz for SICCI-25km, instead of 19.3 GHz for OSI-450 (less noise contribution from atmospheric water vapour content), and 6.9 GHz for SICCI-50km (lower sensitivity to atmosphere and surface snow and sea-ice property variations).
Thus, the results summarized in Fig. 12 indicate that the uncertainty σtot provided with the three CDRs are slightly underestimated, especially for OSI-450 for the high sea-ice concentration range (SIC = 100 %), and are slightly overestimated for the low sea-ice concentration range (SIC = 0 %). The SIC total uncertainty σtot has contributions from the algorithm uncertainty σalgo and the smearing uncertainty σsmear. Because the locations for ground-truth estimates are generally not at the ice edge, the smearing uncertainty term is close to zero and σalgo dominates the evaluation results summarized in Fig. 12. As introduced in Sect. 3.5, the algorithm uncertainty is computed as the standard deviation of the retrieval error at the dynamically selected training data samples. For SIC = 100 % cases, the dynamically selected training samples are spread mostly all over the high sea-ice concentration regions, and there are thus good odds that the training samples are representative of the geophysical conditions in the ground-truth data set, and that in turn the reported uncertainties are in agreement with the retrieval errors for SIC = 100 % cases. For SIC = 0 %, the ground-truth open-water locations are selected just outside the maximum sea-ice climatology, while we used an expanded version of this climatology for the selection of the open-water training data samples (Sect. 3.3 and 3.6). The OW training samples thus generally correspond to lower-latitude conditions (ocean surface, and atmosphere conditions) than the ground-truth locations. For example, training samples may be selected in regions of more frequent synoptic low-pressure paths than the conditions that really prevail at the ice edge and where the ground-truth estimates used in the section are located. A more developed sea state as well as a wetter atmosphere contribute to the overestimation of σalgo (hence σtot) by at maximum 1 % SIC (1 standard deviation) in SIC = 0 % conditions. Finally, we note that the results from Fig. 12 cover the end of the time period (the AMSR-E and AMSR2 years), while the maximum ice extent climatology driving the selection of training samples is computed for almost the whole of 40 years of the sea-ice data record. Trends in sea-ice decline (in the NH, especially summer) might thus have an amplification effect on the overestimation of the uncertainties, as the location for selecting training samples is increasingly further away from the sea-ice edge as decades pass.
4.3 Caveats and known limitations
Known limitations of the SIC CDR are listed in this section. All the aspects listed below apply generally to the other existing SIC data records based on PMW satellite data. Not all of these limitations are reflected in the uncertainty fields of the CDR, as presented below.
The open-water filter (a.k.a. weather filter) implemented in the new SIC CDR is based on a combination of the frequency channels around 19 and 37 GHz (Sect. 3.4.2). Although the filter is efficient at detecting and removing weather-induced noise (false ice) over open water, it also has the effect of removing some amount of true low-concentration ice, especially in the marginal ice zone. Although dynamic tuning strategies were developed for these new CDRs, users are explicitly warned to pay close attention to filtered conditions, especially close to the ice edge. The unfiltered (raw) SIC values can always be accessed in the field raw_ice_conc_values (Sect. 4.1, Fig. 6). The effect of the OWF is not included in the uncertainty variables, which pertain to the unfiltered (raw) ice concentration values. See also the discussion on the temporal consistency of the OWF for the three CDRs in Sect. 4.2.1.
All SIC algorithms based on the passive microwave data are very sensitive to melt-pond water on top of the ice (Kern et al., 2016). The radiation emitted at the wavelengths of the frequency channels comes from a very thin layer at the surface of the melt pond, which does not enable ocean water (in leads and openings) and meltwater (in ponds) to be distinguished. The ice_conc variable of the SIC CDRs should thus hold an estimate of 1 minus the open-water fraction in each grid cell, irrespective of whether this water is from lead and openings or ponds. The misinterpretation of meltwater on top of sea ice as open water is not included in the uncertainty variables (Q. Yang et al., 2016). The uncertainties embedded in the files are those for 1 minus the open-water fraction.
Due to many factors (including smooth surface, absence of snow, brine content) concentration of thin sea-ice (<30 cm) is underestimated by most of the PMW SIC algorithms (Cavalieri, 1994). A complete, 100 % cover of thin sea ice will be retrieved with a lower concentration, depending on the thickness (Ivanova et al., 2015). The effect of thin sea ice is not included in the uncertainty fields of the SIC CDRs.
The SIC data records aim to address needs from a wide range of users, from the interested general public to climate modellers and climate services. It was decided to provide interpolated sea-ice concentration values in places where original input satellite data were missing, aiming to produce the most complete daily maps possible. Both temporal and spatial interpolations are used (Sect. 3.6). The locations where interpolation is used are clearly identified in the status_flag layer. These interpolated sea-ice concentration values should generally be used with caution for scientific applications, especially the values obtained from spatial interpolation. The uncertainty variables are not interpolated where data were missing. Days on which no satellite data were available, e.g. every other day in the SMMR time period, are not interpolated and corresponding files are missing from the data records.
OSI-450 is presented at 25 km grid spacing. However, a spatial sampling of 25 km does not fully represent the true spatial resolution of the product since the footprints of the SMMR, SSM/I, and SSMIS channels used by the algorithms are coarser (Table 2). The mismatch of grid spacing to the true resolution of the instrument footprint is taken into account in the uncertainty model of the OSI SAF CDR and is a key contribution to the smearing uncertainty (Sect. 3.5). The footprint of the AMSR-E and AMSR2 channels used in the ESA CCI CDRs (SICCI-25km and SICCI-50km) are much more compatible with the 25×25 km (SICCI-25km) and 50×50 km (SICCI-50km) target grids, so that their grid spacing is closer to the true resolution. The true resolution of the SICCI-25km CDR might be slightly better than 25×25 km, but this grid spacing was retained to ease uptake by users and comparison with OSI-450.
The radiometric signature of land is similar to that of sea ice at the wavelengths used for estimating the SIC. Because of the large footprints and the relatively high brightness temperatures of land and ice compared to water, the land signature “spills” into the coastal zone open water and it will falsely appear as intermediate concentration ice. This land-spillover effect is corrected for as described in Sect. 3.6. However, coastal correction procedures are not perfect, and some false sea-ice remains along some coastlines, especially for OSI-450 and SICCI-50km because of the larger footprint of the instruments. By the same token, some true coastal sea ice might be removed by the coastal correction scheme. Users are advised to check the values in the raw_ice_conc_values variable where the SIC estimates before the final coastal correction step are available. The uncertainty variables have larger values in the coastal regions where land spillover effects are detected. See also Sect. 5.2.
Ice resulting from freezing of fresh and brackish waters does not have the same emissivity as that from seawater. The retrieval of ice area fraction in these conditions would call for dedicated tie points (e.g. Ghaffari et al., 2011), which we did not implement here. In addition to the difficulty of computing dynamic tie points over such small areas, it is unclear if such dedicated tie points would make a large difference in the end, because of the combination of many error sources in these closed water bodies (land spillover, thin sea-ice, larger atmospheric influence, etc.). A layer in the status_flag variable indicates fresh and brackish water bodies.
5.1 Discussion
This paper documents three new sea ice concentration (SIC) Climate Data Records (CDR). One is from EUMETSAT OSI SAF (OSI-450) and two are from ESA CCI (SICCI-25km and SICCI-50km). All three share the same algorithm baseline, which is both a continuation of the EUMETSAT OSI SAF SIC approach (Andersen et al., 2006; Tonboe et al., 2016) and a series of innovations contributed to mostly by the ESA CCI activities. The three CDRs are a family of data records that aim to address the GCOS Requirements for the sea-ice essential climate variables (ECVs) (GCOS-IP, 2016). The improvements with respect to earlier versions of the CDRs include (1) using high-quality Fundamental Climate Data Records (FCDR) as input data (Sect. 2.1), (2) a new family of self-tuning, self-optimizing SIC algorithms that dynamically adjust to the input TB data (Sect. 3.2, and 3.3), (3) novel noise reduction and filtering approaches (Sect. 3.4), and (4) per-pixel uncertainty estimates (Sect. 3.5). The product data files are designed so that interested users can revert some of the filtering steps and access the raw output of the SIC algorithms (Sect. 4.1).
The three CDRs are designed to ensure temporal continuity throughout the almost 40 years of passive microwave data records. The OSI-450 data set currently covers 1979 to 2015 with a consistent set of frequencies at 19 and 37 GHz. Conversely to other CDRs (e.g. Meier et al., 2017 and its two algorithm components bootstrap and NasaTeam), the channels around 22 GHz are not used for filtering water vapour contamination. The 23.0 GHz channels of the SMMR instrument have been highly unstable since their launch and eventually ceased to function in March 1985. This is one of the reasons why the Meier et al. (2017) data set only starts with SSM/I F08 on 9 July 1987 as a fully qualified CDR (according to https://nsidc.org/data/g02202, last access: 1 June 2018). A key asset of the algorithms we adopted is that they are self-tuning and self-optimizing to the data, which greatly helps temporal consistency to be achieved between different satellite missions, both in the past and future (discussed later in Outlook, Sect. 5.2).
The self-tuning and self-optimizing algorithms also allowed consistent processing of SIC CDRs from the AMSR-E and AMSR2 instruments. The SICCI-25km is an attempt at closing the gap in spatial resolution between what can be achieved from coarse-resolution sensors like SMMR, SSM/I and SSMIS and the requirements of GCOS for 10–15 km spatial resolution (GCOS-IP, 2016). The almost 15-year record of brightness temperature observations from these two instruments is a key complement to OSI-450.
The decision to produce distinct CDRs, one with SMMR, SSM/I, and SSMIS and the other two with AMSR-E and AMSR2 data, is mainly based on the difference in spatial resolution. Mixing the two types of sensors (coarse resolution with medium resolution) into a single CDR would require careful consideration of the mismatch in spatial resolution and possibly advanced enhanced resolution methods (e.g. Long and Daum, 1998; Long and Brodzik, 2016), which are not used here. It is in any case doubtful whether the resulting single CDR would meet the temporal consistency requirements of many climate applications.
An evaluation of the three CDRs and their uncertainties is reported upon in Sect. 4.2. Time-series plots document that the dynamic tuning of the SIC algorithms and of the OWF perform as expected, and that temporal consistency is mostly achieved despite the changes of channel frequencies and calibration between sensors. Based on similar frequency channels at 19 and 37 GHz, the OSI-450 and SICCI-25km CDRs achieve similar accuracies, both in the time-series plots of internal tuning parameters (Sect. 4.2.1) and when validated against ground-truth (Sect. 4.2.2). Over open water, the retrieval accuracy of these two CDRs is as good as 1.5 % to 2 % SIC (1 standard deviation) and without biases. Over consolidated sea ice, the retrieval accuracy is somewhat poorer (3.5 % to 4 % SIC) and has limited low bias (2 % SIC in NH, 1 % in SH). The SICCI-50km uses a 6 GHz frequency channel instead of 19 GHz. Theoretically 6 GHz is a better channel for estimating sea-ice concentration since the atmosphere is more transparent, the influence of error sources like sea-ice age or snow processes have less influence, and the contrast between ocean and ice is larger. This is confirmed in our evaluation results. Over open water, the retrieval accuracy of SICCI-50km is as good as 1 % to 1.5 % SIC (1 standard deviation). Over consolidated sea ice, the accuracy is better than 2.5 % SIC and the bias is limited to below 1 %. The SICCI-50km is thus the most accurate of our three new CDRs but also has the coarsest spatial resolution due to the large footprint of the 6 GHz channels.
Our evaluation results reveal very similar accuracies in the northern and southern hemispheres, even though the sea-ice conditions can be very different. Regarding algorithm performance, the Arctic is more challenging at first glance. At least two radiometrically different ice types, multi-year ice and first-year ice, and a pronounced seasonal cycle of sea-ice and snow properties during summer with regular widespread occurrence of melt ponds on the ice surface need to be accommodated by the algorithm. Antarctic multi-year ice has a less well-studied and different radiometric signature than Arctic multi-year ice, resulting from other summer melt processes, e.g. melt ponds occur rarely; one could say it differs less from that of first-year ice on the one hand. On the other hand, direct and indirect weather influences, causing an unwanted variation in the retrieved sea-ice concentration, have been quite regional in extent in the Arctic Ocean (largely encompassed by land masses), while these have been a common, widespread phenomenon on Antarctic sea ice (bordered by oceans and at lower latitudes). Therefore, a very similar algorithm performance in both hemispheres is not a surprise and agrees with earlier findings (e.g. Ivanova et al., 2015). We note that, because they automatically tune their coefficients (tie points, plane angle θ, etc.) to the training data specific for each hemisphere, our new algorithms can best adapt to radiometric properties of sea ice being different in both hemispheres.
An analysis of the temporal consistency of the open-water filter (Sect. 4.2.1) also revealed that our dynamic tuning of the OWF does not perform as optimally on the SICCI-50km CDR than on SICCI-25km and OSI-450. This is explained by the larger mismatch in frequency and resolution between the channels entering the SIC algorithms, and those used in computing the OWF (19 and 37 GHz only). We note that the dynamic tuning of the OWF as implemented here secures a quite stable level for the minimum detectable true SIC, of the order of 10 % SIC, on average well below the 15 % SIC threshold commonly used for defining sea-ice extent.
An evaluation of the uncertainties, a key element of the CDRs, is reported on in Sect. 4.2.3. We compare the uncertainty values reported in the product files with the retrieval error of the SIC field in conditions of known 0 % and 100 % SIC. Over 100 % SIC, there is a close correspondence between the reported uncertainty and the observed retrieval noise for both hemispheres. In open-water conditions, the uncertainties provided in the CDR product files overestimate the observed retrieval noise by a couple of SIC percent (in terms of standard deviation). This slight overestimation is probably due to the use of a buffer zone outside of the monthly maximum ice climatology extent that dynamically selects the data samples used to train the algorithms (Sect. 3.3) and derive uncertainties (Sect. 3.5).
5.2 Outlook
The Climate Data Records presented in this manuscript will be further developed and extended in the context of the EUMETSAT OSI SAF. A full reprocessing of the OSI-450, SICCI-25km, and SICCI-50km CDRs is committed to by OSI SAF (version 3 of the CDRs) and should happen in 2021. It will use updated versions of the FCDRs – if available – and the new ERA5 atmosphere reanalysis from the EU C3S (Hersbach and Dee, 2016). At time of writing, no radical change of algorithms and processing steps is foreseen, but our paper identifies several improvements and evolutions that would be beneficial for these upcoming versions, and these are briefly described below.
Although the ESA Climate Change Initiative Sea Ice projects went far in the characterization of the impact that melting and melt ponds have on sea-ice concentration retrievals from passive microwave data (Kern et al., 2016), the question on how to limit and best convey the increased uncertainty to users will benefit from further efforts. Results of an intercomparison between the data set of melt-pond fraction, sea-ice concentration and net sea-ice surface fraction used in Kern et al. (2016) and the three CDRs presented in this paper as well as other available sea-ice concentration products, including those based on NASA-Team and bootstrap algorithms, will be reported in a forthcoming article.
The uncertainty model presented here is already a significant improvement over that used in the previous version of the SIC CDR (Tonboe et al., 2016). Nonetheless, additional research is needed to better quantify the uncertainties and validate that they are fit for purpose. Since the way we derive uncertainties is directly linked to the way we select training data samples, it could be investigated whether selecting training samples closer to the ice edge would improve the uncertainty values and, for example, reduce the slight overestimation of uncertainties at SIC = 0 % conditions documented in Sect. 4.2.3. Another challenging topic is the quantification of cross-correlation scales (both in the temporal and spatial dimensions) necessary to fully aggregate such CDRs at the scales relevant for evaluation of models or higher-level climate indicators (Bellprat et al., 2017).
Despite being from all seasons and in both hemispheres, the validation results presented in this paper cover 0 % and 100 % SIC conditions, but not the intermediate range found in the marginal ice zone due to the lack of high-quality validation data. Results of the evaluation of the three CDRs with independent data, i.e. ship-based visual observations of sea-ice cover and sea-ice area fraction derived from high-resolution optical satellite imagery, have been reported in the Product Validation and Intercomparison Report (PVIR; available from http://cci.esa.int, last access: 1 September 2018) and will also be published in forthcoming articles. These will also include an intercomparison of time series of the sea-ice area (SIA) and extent (SIE) derived from the three CDRs and from other sea-ice concentration products.
From the early assessment of the new CDRs presented here, we can already outline a number of algorithm developments that have the potential to further improve the accuracy of future SIC estimates based on passive microwave data, both in climate and operational applications. The new self-tuning, self-optimizing algorithms introduced in this paper are currently limited to 3-D TB spaces. This is because the optimization of the projection plane is handled via a rotation angle along a 3-D axis, a geometrical concept that is difficult to upscale to more dimensions. The generalization of this optimization to n-D (where n could be any subset of the channels available on a given passive microwave imager) would open to assess all possible TB channel combinations in a systematic manner and maybe unveil algorithms to achieve even better accuracy than the 3-D ones used here. By the same token, it should be investigated whether the concept of a consolidated ice curve (as opposed to an ice line) could be better embedded in SIC algorithms in the future instead of being a correction step applied a posteriori as is the case in our CDRs. A third algorithm development to be investigated is the generalization of the concept of open-water filters (a.k.a. weather filters) to 3-D or even n-D, so that the OWFs are always tuned and computed using the same TB channels as the SIC. This development has the potential to improve the temporal consistency of the OWF at low SIC values across changes of wavelengths and calibration or when using TB channels other than 19 and 37 GHz. Finally, research is needed to assign a true spatial resolution to SIC fields computed from combinations of n TB channels, which are themselves at different spatial resolutions. Some knowledge is embedded in our parameterization of σsmear, but it is currently not enough to choose and fully justify a grid spacing for SIC data records. In any case and even after almost 40 years of routinely available passive microwave observations of the polar regions, the underlying algorithms can still be improved to yield improved accuracy and there is scope for continued research and development in the field.
Other steps in the processing chain can further be improved upon, e.g. the land spillover correction schemes. In Sect. 3.6 we described how land spillover was corrected for in two steps, first through a physically based algorithm on swath TB data (adapted from Maass and Kaleschke, 2010), followed by a statistically based correction of gridded SICs (adapted from Cavalieri et al., 1999). Several factors can have led to the swath-based correction to not be enough. For example, the method relies heavily on the accurate geolocation of the TB measurements; however its uncertainty for the SSM/I and SSMIS instrument is known to be large (Poe et al., 2008) and is not corrected for in the current version of the FCDR (R3) we used (Fennig et al., 2017). We used approximated iFoVs weighting functions instead of eFoVs (see Sect. 2.1) when convolving antenna pattern with the land mask, thus neglecting the effect of the measurement integration period. Finally, strategies to avoid gridding land-contaminated FoVs when building Level 3 maps might help in the future. It will also be beneficial to use objective high-resolution SIC maps from coastal regions to tune the various thresholds embedded in the statistically based correction. To improve further on the land spillover correction will be an objective for upcoming versions of the CDRs.
Another development for using such SIC CDRs to evaluate models and perform Data Assimilation would be the definition and uptake of observation operators (a.k.a. satellite simulators, e.g. Kaminski and Mathieu, 2017). Once the remaining systematic errors (such as underestimation of very thin ice, impact of melt-pond water) have been described and quantified, the next step is for the Earth observation science community to define observation operators. These operators are typically parametric formulations that express the quantity retrieved from EO techniques (in our case the sea-ice concentration values in the CDR) as a combination of physical variables in the model world (e.g. sea-ice area fraction, thickness of sea-ice categories, and area coverage of melt pond). We advocate these operators to be built in a stepwise, pragmatic manner (Lavergne, 2017). This development should happen in complement to building more end-to-end satellite simulators that aim to link the physical variables in the model world directly to satellite radiances.
Thanks to using the C-band channels (4–8 GHz) the SICCI-50km CDR exhibits outstanding sea-ice concentration retrieval accuracy, both at low- and high-concentration range. The usability of this CDR can, however, be challenged by its rather coarse resolution (the 6 GHz channels of AMSR-E have a iFoV of 75×43 km (Table 2) and the CDR is presented on a 50 km grid), which is a direct consequence of the limited antenna diameter of the AMSR-E (2.0 m) and AMSR2 (2.1 m) instruments. Our results fully support that a passive microwave mission measuring at the C-band frequency, and carrying a large-enough antenna to enable ground resolutions better than 15 km (at C-band) would be a clear asset for all-weather, global, daily covering sea-ice concentration mapping for operational applications. At the time of writing, such a satellite mission is under study as a High Priority Candidate Mission for the European Union's Copernicus Space Component Expansion: the Copernicus Imaging Microwave Radiometer (CIMR, https://cimr.eu, last access: 1 September 2018).
A key requirement of GCOS for addressing the needs of the climate modelling community, as well as the Climate Information Services such as the EU Copernicus Marine Environment Monitoring Service (CMEMS, http://marine.copernicus.eu, last access: 1 November 2018) and Copernicus Climate Change Service (C3S, http://climate.copernicus.eu, last access: 1 November 2018), is the seamless extension of the CDRs in the context of operational services. These operational services aim to have the best temporal consistency with the CDRs, but still may have to rely on different data streams. They are referred to as Interim Climate Data Records (ICDR) because they are meant as a temporary extension until a full reprocessing of the CDRs is performed (W. Yang et al., 2016). For the SIC variable, both the EUMETSAT OSI SAF CDR of Tonboe et al. (2016) and the NOAA/NSIDC CDR (since late 2017, version 3) are extended daily by such ICDR. We are naturally working towards starting an operational ICDR for our new CDRs, tentatively by late 2018, with a 16 days latency. The algorithm developments will also be introduced to the operational stream of sea-ice products from the EUMETSAT OSI SAF.
Aside from the technical aspects of reliably running the CDR processing chains on a daily basis, a major challenge that all SIC CDR data producers now face is the end of life for the U.S. Defense Meteorological Satellite Program (DMSP), which has been the workhorse for virtually all sea-ice CDRs since SSM/I F08 in 1987 (Table 2 and Fig. 1). At the time of writing, the Japanese AMSR2 instrument is already past its design lifetime (5 years, launched mid-2012), with no committed successor. For the continuation of the new OSI SAF SIC CDR, we are investigating the quality of the Microwave Radiation Imager (MWRI) on board China's Feng-Yun 3 (FY3) satellites. Preliminary results are encouraging and, when consolidated, will be presented in a follow-up paper. The first satellite of the European Polar System Second Generation (EPS-SG) series to carry a Microwave Imager (MWI) is scheduled for launch in 2023. It can be used to further extend the SIC CDR up until the late 2040s. It is noticeable that EPS-SG MWI implements quite a different channel frequency for Ka-band (26.5–40 GHz): 31.4 GHz instead of 36–37 GHz for SSM/IS and AMSRs (Table 2). However, because our algorithms self-adapt to the data and their calibration, the implementation with MWI should be possible. The impact of using 31.4 GHz instead of 36–37 GHz for sea-ice concentration mapping still needs to be addressed.
5.3 Conclusions
Long-term consistency, traceability, and an evaluation and documentation of uncertainties are arguably the three major properties of any climate-data record. In this contribution, we have described how these requirements are reflected by the algorithm underlying the three new sea-ice concentration climate-data records OSI-450, SICCI-25km, and SICCI-50km.
Long-term consistency is achieved by developing an algorithm that dynamically adjusts to changing environmental conditions and changing satellite sensors. In particular, applying the same algorithm to microwave products based on different frequencies and satellites allows users to combine the advantages of the length of the record of the OSI-450 product with the high true spatial resolution of the SICCI-25km product and/or the low-noise product SICCI-50km.
Traceability of the algorithm and the resulting climate-data records is achieved by a combination of two approaches. First, the final products contain substantial information on the impact of the various processing steps. For example, at every time step they include per-pixel information on the impact of possible filtering. Second, the algorithm and the products are embedded into an operational context. This guarantees ease of a long-term maintenance of these products, but in particular establishes clear rules on version tagging, documentation and availability of the underlying code, which allows other researchers to easily build on our work and to develop it further.
Uncertainties are systematically documented in the final products and have carefully been evaluated. All products contain per-pixel information on uncertainties arising from the algorithm itself at every time step (e.g. sensor noise or residual geophysical noise) and the smearing uncertainty from spatial remapping. This information is particularly helpful for data-assimilation purposes. The evaluation of uncertainties carried out in this paper provides some initial information on the remaining random per-pixel uncertainty, which can be used as an estimate of observational uncertainty, for example during model evaluation or data assimilation. We find in particular that our product has a long-term stable zero bias arising from the dynamical retuning of the tie points.
We hope that by explicitly addressing the three requirements of a climate-data record, our three new sea-ice concentration records and the underlying algorithm will be a helpful resource for the climate-research community.
The three SIC CDRs presented in this study are publicly available and can be accessed by following the DOIs https://doi.org/10.15770/EUM_SAF_OSI_0008 (Toudal Pedersen et al., 2017a), https://doi.org/10.5285/f17f146a31b14dfd960cde0874236ee5 (Toudal Pedersen et al., 2017b), and https://doi.org/10.5285/5f75fcb0c58740d99b07953797bc041e (Toudal Pedersen et al., 2017c); see also Table 1.
TL led the writing in most sections, with contributions from SK (validation plots and discussion, Sect. 4.2) and DN (in Introduction and Conclusions). All authors contributed to the development, processing, or validation of the SIC CDRs.
The authors declare that they have no conflict of interest.
The authors are grateful to Edward Hanna and Doug Smith for sharing insights and software for the dynamic tuning of the Bristol SIC algorithm. Our gratitude goes to the open-source community at large, and especially the maintainers of the Python language and its modules (numpy, scipy, matplotlib, pytroll, etc.).
The SMMR, SSM/I, and SSMIS FCDR (R3) were accessed from the EUMETSAT CM SAF (http://www.cmsaf.eu/, last access: 1 June 2018). Karsten Fennig and Marc Schröder, both at DWD, helped to make the best use of this data. The AMSR-E FCDR was accessed from NSIDC and the AMSR2 data from JAXA. ECMWF ERA-Interim was accessed from the MARS archive.
This study and the development of the three new SIC CDRs were funded by
EUMETSAT (through the 2nd Continuous Developments and Operation Phase of OSI
SAF) and ESA (through the Climate Change Initiative SeaIce_cci
project).
Edited by: Chris
Derksen
Reviewed by: two anonymous referees
Andersen, S., Tonboe, R., Kern, S., and Schyberg, H.: Improved retrieval of sea ice total concentration from spaceborne passive microwave observations using Numerical Weather Prediction model fields: An intercomparison of nine algorithms, Remote Sens. Environ., 104, 374–392, 2006.
Andersen, S., Toudal Pedersen, L., Heygster, G., Tonboe, R., and Kaleschke, L.: Intercomparison of passive microwave sea ice concentration retrievals over the high concentration Arctic sea ice, J. Geophys. Res., 112, C08004, https://doi.org/10.1029/2006JC003543, 2007.
Ashcroft, P. and Wentz, F. J.: AMSR-E/Aqua L2A Global Swath Spatially-Resampled Brightness Temperatures, Version 3 [2002–2010], NASA National Snow and Ice Data Center Distributed Active Archive Center, Boulder, Colorado, USA, https://doi.org/10.5067/AMSR-E/AE_L2A.003, 2013.
Bellprat, O., Massonnet, F., Siegert, S., Prodhomme, C., Macias-Gómez, D., Guemas, V., and Doblas-Reyes, F.: Uncertainty propagation in observational references to climate model scales, Remote Sens. Environ., 203, 101–108, https://doi.org/10.1016/j.rse.2017.06.034, 2017.
Brodzik, M. J., Billingsley, B., Haran, T., Raup, B., and Savoie, M. H.: EASE-Grid 2.0: Incremental but Significant Improvements for Earth-Gridded Data Sets, ISPRS Int. Geo.-Inf., 1, 32–45, https://doi.org/10.3390/ijgi1010032, 2012.
Brodzik, M. J., Billingsley, B., Haran, T., Raup, B., and Savoie, M. H.: Correction: Brodzik, M. J. et al.: EASE-Grid 2.0: Incremental but Significant Improvements for Earth-Gridded Data Sets, ISPRS Int. Geo.-Inf., 1, 32–45, 2012, ISPRS Int. Geo.-Inf., 3, 1154–1156, https://doi.org/10.3390/ijgi3031154, 2014.
Brooks, C. E. P.: The Problem of Warm Polar Climates, Q. J. Roy. Meteor. Soc., 51, 83–91, 1925.
Cavalieri, D. J., Gloersen, P., and Campbell, W. J.: Determination of Sea Ice Parameters With the NIMBUS 7 SMMR, J. Geophys. Res., 89, 5355–5369, 1984.
Cavalieri, D. J., Crawford, J., Drinkwater, M., Emery, W. J., Eppler, D. T., Farmer, L. D., Goodberlet, M., Jentz, R., Milman, A., Morris, C., Onstott, R., Schweiger, A., Shuchman, R., Steffen, K., Swift, C. T., Wackerman, C., and Weaver, R. L.: NASA sea ice validation program for the DMSP SSM/I: final report, NASA Technical Memorandum 104559, National Aeronautics and Space Administration, Washington, D.C., 126 pp., 1992.
Cavalieri, D. J.: A microwave technique for mapping thin sea ice, J. Geophys. Res., 99, 12561–12572, 1994.
Cavalieri, D. J., St. Germain, K. M., and Swift, C. T.: Reduction of weather effects in the calculation of sea ice concentration with the DMSP SSM/I, J. Glaciol., 41, 455–464, 1995.
Cavalieri, D. J., Parkinson, C. L., Gloersen, P., Comiso, J. C., and Zwally, H. J.: Deriving long-term time series of sea ice cover from satellite passive-microwave multisensor data sets, J. Geophys. Res., 104, 15803–15814, https://doi.org/10.1029/1999JC900081, 1999.
Colton, M. C. and Poe, G. A.: Intersensor calibration of DMSP SSM/Is: F-8 to F-14, 1987–1997, IEEE T. Geosci. Remote, 37, 418–439, 1999.
Comiso, J. C.: Characteristics of arctic winter sea ice from satellite multispectral microwave observations, J. Geophys. Res., 91, 975–994, 1986.
Comiso, J. C. and Nishio, F.: Trends in the sea ice cover using enhanced and compatible AMSR-E, SSM/I, and SMMR data, J. Geophys. Res., 113, C02S07, https://doi.org/10.1029/2007JC004257, 2008.
Comiso, J. C., Gersten, R. A., Stock, L. V., Turner, J., Perez, G. J., and Cho, K.: Positive Trend in the Antarctic Sea Ice Cover and Associated Changes in Surface Temperature, J. Climate, 30, 2251–2267, https://doi.org/10.1175/JCLI-D-16-0408.1, 2017a.
Comiso, J. C.: Large Decadal Decline of the Arctic Multiyear Ice Cover, J. Climate, 25, 1176–1193, https://doi.org/10.1175/JCLI-D-11-00113.1, 2012.
Comiso, J. C., Meier, W. N., and Gersten, R.: Variability and trends in the Arctic Sea ice cover: Results from different techniques, J. Geophys. Res.-Oceans, 122, 6883–6900, 2017b.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, 2011.
Donlon, C. J., Martin, M., Stark, J. D., Roberts-Jones, J., Fiedler, E., and Wimmer, W.: The Operational Sea Surface Temperature and Sea Ice analysis (OSTIA), Remote Sens. Environ., 116, 140–158, https://doi.org/10.1016/j.rse.2010.10.017, 2012.
Fennig, K., Schröder, M., and Hollmann, R.: Fundamental Climate Data Record of Microwave Imager Radiances, Edition 3, Satellite Application Facility on Climate Monitoring, https://doi.org/10.5676/EUM_SAF_CM/FCDR_MWI/V003, 2017.
GCOS-IP: GCOS Implementation Plan 2016, GCOS-200, available at: https://library.wmo.int/opac/doc_num.php?explnum_id=3417 (last access: 1 November 2018), 2016.
Ghaffari, P., Pedersen, L., Eastwood, S., and Lavergne, T.: Sea Ice in the Caspian Sea, Technical Report OSI_AS11_P04, available at: https://osisaf.met.no (last access: 1 November 2018), 2011.
Gregory, J. M., Stott, P. A., Cresswell, D. J., Rayner, N. A., Gordon, C., and Sexton, D. M. H.: Recent and Future Changes in Arctic Sea Ice Simulated by the HadCM3 AOGCM, Geophys. Res. Lett. 29, 2175, https://doi.org/10.1029/2001GL014575, 2002.
Herrington, T. and Zickfeld, K.: Path independence of climate and carbon cycle response over a broad range of cumulative carbon emissions, Earth Syst. Dynam., 5, 409–422, https://doi.org/10.5194/esd-5-409-2014, 2014.
Hersbach, H. and Dee, D.: ERA5 reanalysis is in production, ECMWF Newsletter, Number 147 – Spring 2016, available at: https://www.ecmwf.int/en/newsletter/147/news/era5-reanalysis-production (last access: 1 November 2018), 2016.
Hobbs, W., Massom, R., Stammerjohn, S., Reid, P., Williams, G., and Meier, W.: A review of recent changes in Southern Ocean sea ice, their drivers and forcings, Global Planet. Change, 143, 228–250, https://doi.org/10.1016/j.gloplacha.2016.06.008, 2016.
Ivanova, N., Pedersen, L. T., Tonboe, R. T., Kern, S., Heygster, G., Lavergne, T., Sørensen, A., Saldo, R., Dybkjær, G., Brucker, L., and Shokr, M.: Inter-comparison and evaluation of sea ice algorithms: towards further identification of challenges and optimal approach using passive microwave observations, The Cryosphere, 9, 1797–1817, https://doi.org/10.5194/tc-9-1797-2015, 2015.
Johannessen, O. M.: Decreasing Arctic Sea Ice Mirrors Increasing CO2 on Decadal Time Scale, Atmospheric and Oceanic Science Letters, 1, 51–56, https://doi.org/10.1080/16742834.2008.11446766, 2008.
Kaminski, T. and Mathieu, P.-P.: Reviews and syntheses: Flying the satellite into your model: on the role of observation operators in constraining models of the Earth system and the carbon cycle, Biogeosciences, 14, 2343–2357, https://doi.org/10.5194/bg-14-2343-2017, 2017.
Kern, S., Rösel, A., Pedersen, L. T., Ivanova, N., Saldo, R., and Tonboe, R. T.: The impact of melt ponds on summertime microwave brightness temperatures and sea-ice concentrations, The Cryosphere, 10, 2217–2239, https://doi.org/10.5194/tc-10-2217-2016, 2016.
Korosov, A. A., Rampal, P., Pedersen, L. T., Saldo, R., Ye, Y., Heygster, G., Lavergne, T., Aaboe, S., and Girard-Ardhuin, F.: A new tracking algorithm for sea ice age distribution estimation, The Cryosphere, 12, 2073–2085, https://doi.org/10.5194/tc-12-2073-2018, 2018.
Kwok, R.: Sea ice concentration estimates from satellite passive microwave radiometry and openings from SAR ice motion, Geophys. Res. Lett., 29, 1311, https://doi.org/10.1029/2002GL014787, 2002.
Lavergne, T., Eastwood, S., Teffah, Z., Schyberg, H., and Breivik, L.-A.: Sea ice motion from low-resolution satellite sensors: An alternative method and its validation in the Arctic, J. Geophys. Res., 115, C10032, https://doi.org/10.1029/2009JC005958, 2010.
Lavergne, T.: A step back is a move forward, figshare, 16 October 2017, https://doi.org/10.6084/m9.figshare.5501536.v1, 2017.
Long, D. G. and Daum, D. L.: Spatial resolution enhancement of SSM/I data, IEEE T. Geosci. Remote, 36, 407–417, 1998.
Long, D. G. and Brodzik, M. J.: Optimum Image Formation for Spaceborne Microwave Radiometer Products, IEEE T. Geosci. Remote, 54, 2763–2779, https://doi.org/10.1109/TGRS.2015.2505677, 2016.
Lu, J., Heygster, G., and Spreen, G.: Atmospheric Correction of Sea Ice Concentration Retrieval for 89 GHz AMSR-E Observations, IEEE J-STARS., 11, 1442–1457, https://doi.org/10.1109/JSTARS.2018.2805193, 2018.
Maass, N. and Kaleschke, L. Improving passive microwave sea ice concentration algorithms for coastal areas: applications to the Baltic Sea, Tellus A, 62, 393–410, https://doi.org/10.1111/j.1600-0870.2010.00452.x, 2010.
Mahlstein, I. and Knutti, R.: September Arctic sea ice predicted to disappear near 2 ∘C global warming above present, J. Geophys. Res., 117, D06104, https://doi.org/10.1029/2011JD016709, 2012.
Maykut, G. A.: Energy Exchange over Young Sea Ice in the Central Arctic, J. Geophys. Res.-Oceans, 83, 3646–3658, https://doi.org/10.1029/JC083iC07p03646, 1978.
Meier, W., Fetterer, F., Savoie, M., Mallory, S., Duerr, R., and Stroeve, J.: NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration, Version 3, NSIDC: National Snow and Ice Data Center, Boulder, Colorado, USA, https://doi.org/10.7265/N59P2ZTG, 2017.
Meier, W. N. and Ivanoff, A.: Intercalibration of AMSR2 NASA Team 2 Algorithm Sea Ice Concentrations With AMSR-E Slow Rotation Data, in: IEEE J.-Stars, 10, 1–11, https://doi.org/10.1109/JSTARS.2017.2719624, 2017.
Merchant, C. J., Paul, F., Popp, T., Ablain, M., Bontemps, S., Defourny, P., Hollmann, R., Lavergne, T., Laeng, A., de Leeuw, G., Mittaz, J., Poulsen, C., Povey, A. C., Reuter, M., Sathyendranath, S., Sandven, S., Sofieva, V. F., and Wagner, W.: Uncertainty information in climate data records from Earth observation, Earth Syst. Sci. Data, 9, 511–527, https://doi.org/10.5194/essd-9-511-2017, 2017.
Niederdrenk, A.-L. and Notz, D.: Arctic Sea Ice in a 1.5 ∘C Warmer World, Geophys. Res. Lett., 45, 1963–1971, https://doi.org/10.1002/2017GL076159, 2018.
Njoku, E. G., Rague, B., and Fleming, K.: The Nimbus-7 SMMR Pathfinder Brightness Temperature Data Set, Jet Propulsion Laboratory Publication, Pasadena, USA, 98-4, 1998.
Notz, D. and Marotzke, J.: Observations reveal external driver for Arctic sea-ice retreat, Geophys. Res. Lett., 39, L08502, https://doi.org/10.1029/2012GL051094, 2012.
Notz, D. and Stroeve, J.: Observed Arctic Sea-Ice Loss Directly Follows Anthropogenic CO2 Emission, Science, 354, 747–750, https://doi.org/10.1126/science.aag2345, 2016.
Pedersen, L. T., Saldo, R., Ivanova, N., Kern, S., Heygster, G., Tonboe, R., Huntemann, M., Ozsoy, B., Ardhuin, F., and Kaleschke, L.: Reference dataset for sea ice concentration, https://doi.org/10.6084/m9.figshare.6626549.v3, 2018.
Poe, G. A., Uliana, E. A., Gardiner, B. A., von Rentzell, T. E., and Kunkee, D. B.: Geolocation Error Analysis of the Special Sensor Microwave Imager/Sounder, in: IEEE T. Geosci. Remote, 46, 913–922, https://doi.org/10.1109/TGRS.2008.917981, 2008.
Sigmond, M., Fyfe, J. C., and Swart, N. C.: Ice-Free Arctic Projections under the Paris Agreement, Nat. Clim. Change, 8, 404–408, https://doi.org/10.1038/s41558-018-0124-y, 2018.
Screen, J. A. and Williamson, D: Ice-Free Arctic at 1.5 ∘C?, Nat. Clim. Change., 7, 230–31, https://doi.org/10.1038/nclimate3248, 2017.
Smith, D. M. and Barrett, E. C.: Satellite mapping and monitoring of sea ice, CB/RAE/9/2/4/2034/113/ARE, RSU, University of Bristol, Bristol, UK, 1994.
Smith, D. M.: Extraction of winter total sea ice concentration in the Greenland and Barents Seas from SSM/I data, Int. J. Remote Sens., 17, 2625–2646, 1996.
Spreen, G., Kaleschke, L., and Heygster, G.: Sea ice remote sensing using AMSR-E 89-GHz channels, J. Geophys. Res., 113, C02S03, https://doi.org/10.1029/2005JC003384, 2008.
Strong, C. and Golden, K. M.: Filling the Polar Data Gap in Sea Ice Concentration Fields Using Partial Differential Equations, Remote Sens., 8, 442, https://doi.org/10.3390/rs8060442, 2016.
Tonboe, R. T., Eastwood, S., Lavergne, T., Sørensen, A. M., Rathmann, N., Dybkjær, G., Pedersen, L. T., Høyer, J. L., and Kern, S.: The EUMETSAT sea ice concentration climate data record, The Cryosphere, 10, 2275–2290, https://doi.org/10.5194/tc-10-2275-2016, 2016.
Toudal Pedersen, L., Dybkjær, G., Eastwood, S., Killie, M. A., Lavelle, J., Lavergne, T., Pfeiffer, H., Sørensen, A., and Tonboe, R.: EUMETSAT SAF on Ocean and Sea Ice, Global Sea Ice Concentration Climate Data Record v2.0 – Multimission, OSI SAF, https://doi.org/10.15770/EUM_SAF_OSI_0008, 2017a.
Toudal Pedersen, L., Dybkjær, G., Eastwood, S., Heygster, G., Ivanova, N., Kern, S., Lavergne, T., Saldo, R., Sandven, S., Sørensen, A., and Tonboe, R.: ESA Sea Ice Climate Change Initiative (Sea_Ice_cci): Sea Ice Concentration Climate Data Record from the AMSR-E and AMSR-2 instruments at 25 km grid spacing, version 2.1, Centre for Environmental Data Analysis, https://doi.org/10.5285/f17f146a31b14dfd960cde0874236ee5, 5 October 2017b.
Toudal Pedersen, L., Dybkjær, G., Eastwood, S., Heygster, G., Ivanova, N., Kern, S., Lavergne, T., Saldo, R., Sandven, S., Sørensen, A., and Tonboe, R.: ESA Sea Ice Climate Change Initiative (Sea_Ice_cci): Sea Ice Concentration Climate Data Record from the AMSR-E and AMSR-2 instruments at 50 km grid spacing, version 2.1, Centre for Environmental Data Analysis, https://doi.org/10.5285/5f75fcb0c58740d99b07953797bc041e, 5 October 2017c.
Wentz, F. J.: A model function for ocean microwave brightness temperatures, J. Geophys. Res., 88, 1892–1908, https://doi.org/10.1029/JC088iC03p01892, 1983.
Wentz, F. J.: A well-calibrated ocean algorithm for SSM/I, J. Geophys. Res., 102, 8703–8718, https://doi.org/10.1029/96JC01751, 1997.
Wentz, F. J. and Meissner, T.: AMSR ocean algorithm version 2, RSS Tech, Proposal 121599A-1, Remote Sensing Systems, Santa Rosa, California, 2000.
Yang, Q., Losch, M., Losa, S. N., Jung, T., Nerger, L., and Lavergne, T.: Brief communication: The challenge and benefit of using sea ice concentration satellite data products with uncertainty estimates in summer sea ice data assimilation, The Cryosphere, 10, 761–774, https://doi.org/10.5194/tc-10-761-2016, 2016.
Yang, W., John, V. O., Zhao, X., Lu, H., and Knapp, K. R.: Satellite Climate Data Records: Development, Applications, and Societal Benefits, Remote Sens., 8, 331, https://doi.org/10.3390/rs8040331, 2016.
Zickfeld, K., Arora, V. K., and Gillett, N. P.: Is the climate response to CO2 emissions path dependent?, Geophys. Res. Lett., 39, L05703, https://doi.org/10.1029/2011GL050205, 2012.





