the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Ice island thinning: rates and model calibration with in situ observations from Baffin Bay, Nunavut
Derek Mueller
Gregory Crocker
Laurent Mingo
Luc Desjardins
Dany Dumont
Marcel Babin
A 130 km2 tabular iceberg calved from Petermann Glacier in northwestern Greenland on 5 August 2012. Subsequent fracturing generated many individual large “ice islands”, including Petermann ice island (PII)-A-1-f, which drifted between Nares Strait and the North Atlantic. Thinning caused by basal and surface ablation increases the likelihood that these ice islands will fracture and disperse further, thereby increasing the risk to marine transport and infrastructure as well as affecting the distribution of freshwater from the polar ice sheets. We use a unique stationary and mobile ice-penetrating radar dataset collected over four campaigns to PII-A-1-f to quantify and contextualize ice island surface and basal ablation rates and calibrate a forced convection basal ablation model. The ice island thinned by 4.7 m over 11 months. The majority of thinning (73 %) resulted from basal ablation, but the volume loss associated with basal ablation was ∼12 times less than that caused by areal reduction (e.g. wave erosion, calving, and fracture). However, localized thinning may have influenced a large fracture event that occurred along a section of ice that was ∼40 m thinner than the remainder of the ice island. The calibration of the basal ablation model, the first known to be conducted with field data, supports assigning the theoretically derived value of 1.2×10−5 m2∕5 s ∘C−1 to the model's bulk heat transfer coefficient with the use of an empirically estimated ice–ocean interface temperature. Overall, this work highlights the value of systematically collecting ice island field data for analyzing deterioration processes, assessing their connections to ice island morphology, and adequately developing models for operational and research purposes.
- Article
(11812 KB) -
Supplement
(118 KB) - BibTeX
- EndNote
A nascent “ice island” is currently being monitored as transverse rifts propagate and widen across the floating ice tongue of Petermann Glacier, northwestern Greenland (USGS, 2019). Ice shelves and ice tongues in this region episodically calve these large, tabular icebergs, which are morphologically similar to those common in the Antarctic although thinner and less extensive (Higgins, 1989). Through their drift and deterioration, these ice islands disperse freshwater between Nares Strait and the North Atlantic (Crawford et al., 2018b). Their journey to southern latitudes can be disrupted due to grounding on the continental shelf of Baffin Island (Crawford et al., 2018a). Such groundings can disrupt benthic ecosystems (Dowdeswell and Bamber, 2007), put seafloor infrastructure at risk (Fuglem and Jordaan, 2017), extend and stabilize landfast ice cover offshore (Fraser et al., 2012; Massom et al., 2001), and impact the biological and physical composition of ocean waters in their vicinity due to meltwater input and latent heat uptake resulting from their deterioration (Jansen et al., 2007; Stern et al., 2015).
Ice island thinning has previously been estimated via freeboard monitoring with satellite-borne altimetry data (Bouhier et al., 2018; Jansen et al., 2007). Without field observations, the individual contribution of surface versus basal ablation to that thinning can then only be derived through modelling (Ballicater Consulting, 2012; Jansen et al., 2007), often with a relatively simple fluid-dynamics approach being used to model basal ablation in iceberg and ice island studies (Ballicater Consulting, 2012; Merino et al., 2016; Wagner and Eisenman, 2017). This forced convection model is based on the transfer of heat across a flat plate due to the turbulent flow of the underlying water. A bulk heat transfer coefficient is used to estimate an ablation rate based on the differential velocity between the ice island and the ocean current as well as the water temperature across the length of the ice island (Ballicater Consulting, 2012; Bouhier et al., 2018; Weeks and Campbell, 1973). Previous efforts to calibrate basal ablation models have relied upon remotely sensed datasets as well as potentially inaccurate modelled environmental data (Bouhier et al., 2018; Jansen et al., 2007). This is largely due to the challenges associated with collecting field data for determining the individual rates of surface and basal ablation.
We overcame these challenges to collect a unique dataset from Petermann ice island (PII)-A-1-f between November 2015 and September 2016. PII-A-1-f was grounded on the continental shelf of Baffin Island and had a surface areal extent of 13 km2 when it was first visited. The fieldwork included repeat mobile ice-penetrating radar (mIPR) transects and the collection of a long-term in situ dataset of ice island thinning by a stationary IPR (sIPR). These were the first such field data to be collected from an ice island or iceberg in either the Arctic or Antarctic. The measurements are used to calibrate the forced convection basal ablation model, which had previously not been validated or calibrated with direct field observations. In addition, the IPR data were used to assess the spatial and temporal variation in ice island thinning and ablation rates. Using remotely sensed imagery to monitor areal reduction, the ablation magnitudes are put into context with respect to other processes (e.g. fracture) that contributed to the deterioration of PII-A-1-f.
PII-A-1-f was a fragment of the 130 km2 PII that calved from Petermann Glacier in northwestern Greenland on 5 August 2012 (Crawford et al., 2018a). Using tracking data derived from RADARSAT-2 satellite images in the Canadian Ice Island Drift, Deterioration and Detection (CI2D3) Database (Crawford et al., 2018a) and by the Canadian Ice Service (CIS; Environment and Climate Change Canada) we were able to trace the origins of PII-A-1-f as the PII broke up and drifted through Nares Strait and Baffin Bay between August 2012 and November 2014. As this piece drifted south, it further fragmented and experienced periods of stagnation while grounded in Kane Basin and northern Baffin Bay (Fig. 1a). The PII-A-1-f fragment entered northern Baffin Bay in late 2013. Continued monitoring with RADARSAT-2 acquisitions showed that a portion of the deterioration that PII-A-1-f experienced after 2013 was caused by sidewall notches that progressively enlarged on opposing sides of the ice island. The notch “roots”, or the tips of these wedge-shaped features, were located in the vicinity of a linear surface feature that was identified in a ScanSAR acquisition in November 2012 (Fig. 1b). This deterioration was likely caused by increased wave-induced turbulent heat flux within these wedge-shaped features as described by White et al. (1980).
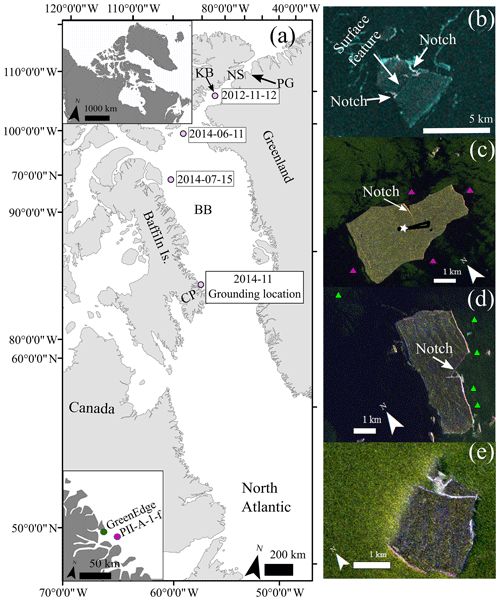
Figure 1Remote monitoring of PII-A-1-f and data collection locations. (a) Dates and locations of PII-A-1-f as observed with RADARSAT-2 synthetic aperture radar (SAR) observations while the ice island drifted from the Petermann Glacier (PG) and through Nares Strait (NS), Kane Basin (KB), and Baffin Bay (BB) before grounding north of the Cumberland Peninsula (CP). The polygon in the top inset shows the location of the larger-scale map. The bottom inset shows the proximity of the grounding location to the GreenEdge sea ice camp. (b) RADARSAT-2 ScanSAR image (100 m nominal resolution) showing the surface feature and sidewall notches. (c–e) RADARSAT-2 Fine Quad SAR (8 m nominal resolution) scenes acquired on 27 June 2016, 27 September 2016, and 23 September 2017, respectively. CTD (conductivity, temperature, depth) cast locations are denoted by triangles in (c) and (d), and the star in (c) denotes the location of the stationary ice-penetrating radar and weather station; the ∼3 km mobile IPR transect conducted in May 2016 is shown as a black line. All RADARSAT-2 images are presented as colour composites (ScanSAR polarizations: red is HH and blue and green is HV; Fine Quad polarizations: red is HH, green is VV, and blue is HV).
The linear surface feature and one sidewall notch were still apparent when PII-A-1-f became grounded in November 2014 at 67∘23′ N, 63∘18′ W, approximately 10 km from the eastern coast of Baffin Island and 35 km southeast from the Hamlet of Qikiqtarjuaq, Nunavut (Fig. 1a). Ice island groundings are especially common in the region immediately north of the Cumberland Peninsula due to the presence of many underwater shoals and ridges. PII-A-1-f was visited at this location by three field teams, with transportation provided by the CCGS Amundsen icebreaker and its helicopter during the annual ArcticNet science cruises in October 2015, July 2016, and September 2016. An additional field campaign was completed in May 2016, when a field team accessed the ice island, then surrounded by sea ice, by a snowmobile from Qikiqtarjuaq, Nunavut.
3.1 Thinning (temporal assessment)
To ascertain the magnitudes and rates of surface and basal ablation, a series of ablation stakes, a 40 MHz sIPR, and a small meteorological station with a sonic ranger and camera were installed on PII-A-1-f on 20 October 2015 (Fig. 2). The ice island position was recorded hourly with a Garmin 6X-HVS GPS (Garmin International, Inc.), and air temperature (Ta) was measured with a 109 thermistor (Campbell Scientific Canada Corporation – CSCC) in a radiation shield at 1 min intervals and logged as hourly averages. All meteorological station data were recorded on a CR1000 data logger (CSCC) and telemetered with an Iridium L-Band modem (9522B; CSCC).
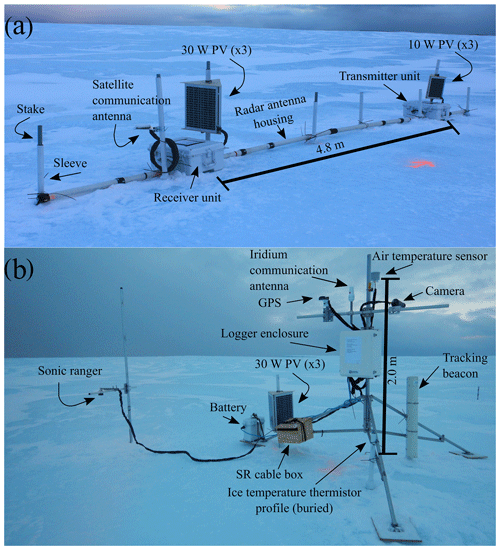
Figure 2Instruments installed on PII-A-1-f on 20 October 2015. (a) Stationary ice-penetrating radar (sIPR) components deployed with antennas “in line” and attached to eight sleeves that slid over stake anchors. (b) Automatic weather station components, including a camera that acquired a weekly image of the sIPR and ablation stakes (not shown). The two systems were installed 30 m apart on two small ridges at the location denoted in Fig. 1c. PV is photovoltaic panel; SR is sonic ranger.
Ice thickness was recorded and telemetered daily by the sIPR (Blue System Integration, Ltd.) until 27 September 2016. Full details regarding this system set-up and measurement specifications can be found in S1 and Mingo et al. (2020). The ice thickness was measured at a resolution of 0.67 m, so the observations were linearly interpolated between dates when step changes in thickness were recorded (16 November 2015–18 September 2016). These dates were used to establish “calibration intervals” for the calibration of the forced convection basal ablation described in the following section.
Daily mean surface ablation was calculated from hourly SR50A sonic ranger (CSCC) height-above-surface (snow or ice) measurements. Surface ablation was also calculated from five ablation stakes that were marked with tape every 10 cm and placed between the meteorological station and the sIPR. A weekly image acquired with a Campbell Scientific CC5MPX camera that was controlled by the meteorological station to visually check on the positioning of the sIPR system also captured these ablation stakes. No snow was present on the date when the stakes and instruments were installed, and the average weekly ablation (or accumulation) at these stakes was calculated with ImageJ (v. 10.8.0) software using the markings for scale (Abramoff et al., 2004). Increases in surface height due to the accumulation of snow are presented in this study as negative values. A linear interpolation was applied to estimate daily ablation or accumulation between these observations so that the sIPR, SR50A, and ablation stake data were available over a consistent time span. Basal ablation was calculated by subtracting the interpolated ablation magnitudes derived from the stake data from the ice thickness time series. These values are therefore approximations of daily basal ablation rates, as they were based on values of ice thickness that were linearly interpolated across longer time periods. Finally, the ablation stake data were used instead of the SR50A data because an unrealistic basal ablation time series was derived from the SR50A data. This was likely caused by a difference in surface conditions between the sIPR and SR50A. It was not possible to assess the surface conditions at the SR50A (30 m away from the sIPR), while the surface conditions were confirmed to be similar between the locations of the ablation stakes and the sIPR (10–15 m away) in weekly images.
3.2 Basal ablation model calibration
3.2.1 Oceanographic data collection and comparison
The derived basal ablation was used to calibrate the forced convection model described in the Introduction. In addition to the general paucity of ice island thinning measurements, there is a dearth of in situ oceanographic data available for the validation and calibration of iceberg and ice island numerical deterioration models. Here, we use two oceanographic field datasets to validate and calibrate a time series of modelled ocean temperature, salinity, and current data that spans the full duration for which basal ablation rates were available. Using the oceanographic model data greatly extended the time span over which the model calibration could be conducted.
The first oceanographic field dataset was collected by the CCGS Amundsen during its annual ArcticNet science research cruise. CTD (conductivity, temperature, depth) profiles were conducted around PII-A-1-f on 28 July (four casts) and 29 September (five casts) 2016 (Amundsen Science Data Collection, 2016; Fig. 1c, d). CTD profiles were also collected on 29 July 2016 (two casts) and 28 September 2016 (one cast) close to the location of a sea ice camp that was situated 20 km northwest (67∘29′ N, 63∘47′ W) of the grounding location of PII-A-1-f (Fig. 1a, bottom inset). This sea ice camp was operated by the GreenEdge project based out of Université Laval, Québec. The second oceanographic field dataset was composed of 39 CTD profiles (SBE 49 FastCAT CT; Sea-Bird Electronics, Inc.) acquired at the GreenEdge sea ice camp between 20 April and 22 July 2016. Absolute salinity (SA; g kg−1) and conservative temperature (Θ; ∘C) measurements were reported at 1 m depth bins for all CTD casts. Current speed (u; m s−1) was calculated as an average of the current vectors measured every 30 s over 2 m depth bins and recorded every 30 min at the ice camp with a Teledyne RDI Workhorse Sentinel 300 kHz acoustic Doppler current profiler (ADCP; Teledyne RD Instruments; Oziel et al., 2019). A linear interpolation was applied to fill missing values before daily average u was calculated for the individual depth bins.
Data from the Copernicus Marine Environment Monitoring Service (CMEMS) Global Ocean Physical Reanalysis (GLORYS12V1) product were used for the calibration of the forced convection basal ablation model. This reanalysis product, henceforth referred to as the CMEMS data, had a spatial resolution of 1∕12∘ and 50 depth levels. Potential temperature, practical salinity, and the horizontal current velocity components were extracted from the model grid cells that corresponded with the locations of PII-A-1-f and the GreenEdge sea ice camp at the model depth bin in which the keel of the ice island was located over the course of sIPR data collection. Keel depth was calculated using ice thickness assuming ice density (ρi)=873 kg m−3 (Crawford et al., 2018c) and hydrostatic equilibrium. Potential temperature and practical salinity were converted to Θ and SA, respectively, using the Gibbs SeaWater functions provided in the R “gsw” package (Kelly, 2017).
The CMEMS data were compared against the in situ oceanographic data to justify its use for calibrating the forced convection basal ablation model and to identify any bias in the modelled oceanographic data. Comparisons were conducted between (1) the full CCGS Amundsen CTD profiles collected at the location of PII-A-1-f and near the GreenEdge sea ice camp location in July and September 2016, (2) the full CCGS Amundsen profiles and the CMEMS data profiles, and (3) the CMEMS data time series and the mean SA, Θ, and u values of all CTD casts and ADCP measurements that fell within the CMEMS depth bin in which the ice island keel was located. Bias in the CMEMS data was identified as consistent over- or underestimation of the GreenEdge sea ice camp time series of SA, Θ, and u. If bias existed in a given variable, the CMEMS data were corrected by the average daily difference between them and the in situ values.
3.2.2 Model calibration
The forced convection basal ablation model (Eq. 1) estimates an ablation rate (Mb; m d−1) from the velocity difference between the iceberg and the water (Δu; m s−1) and the driving temperature (ΔT) across the length (L; m) of an ice face using a bulk heat transfer coefficient, C (m2∕5 s ∘C−1; Weeks and Campbell, 1973). The multiplier in Eq. (1) (86 400 s d−1) converts Mb from metres per second into a daily ablation value; it is also common to scale C by this factor to produce daily melt estimates directly (e.g. Bigg et al., 1997). In the calibration, it was assumed that the ice island was stationary and therefore Δu is simply equivalent to u. ΔT was calculated as the difference between the ocean temperature at the keel depth and the melting point of ice (equivalent to the freezing point of the adjacent sea water). The melting point (Mp; ∘C) was adjusted to account for the influence of meltwater near the ice–water interface with an established empirical relationship with the far-field water temperature (Θ) and the freezing temperature of the far-field ocean water (Θf; ∘C; Eq. 2; Kubat et al., 2007; Løset, 1993a). Θf was derived with SA and pressure (p; dbar) as per TEOS-10 conventions (IOC, SCOR, and IAPSO, 2010):
Values of C were obtained for each calibration interval i (Ci), which is associated with a measured change in ice thickness. The individual Ci values were calculated by dividing the cumulative basal ablation over the respective calibration interval by the corresponding cumulative driving force (i.e. . The driving force was derived from CMEMS modelled oceanographic data (SA, Θ, and u) at the ice island keel. p was set to the pressure at the keel depth. L was assigned as the median of all distances between the sIPR location and all vertices of the outline of the areal surface extent of PII-A-1-f that was digitized from RADARSAT-2 Fine Quad (FQ; 8 m nominal resolution) SAR imagery acquired on 27 July 2016 (S2).
A second calibration for each interval was conducted with the CMEMS data after corrections were applied based on the comparisons against the in situ oceanographic data (Sect. 3.2.1). A final calibration of C was obtained based on the basal ablation and driving force over the total duration over which basal ablation was derived. This final calibration provided a single value of C as opposed to the previous calibrations where values of Ci were obtained for each calibration interval.
An analysis was conducted to determine the sensitivity of the basal melt magnitude predicted by the forced convection basal ablation model to variations in u, Θ, and C. The two variables and one parameter were individually perturbed across eight equally spaced intervals that covered their observed and calculated ranges. The non-perturbed variables were held constant at their median values. All assigned values were based on the corrected CMEMS data series. The sensitivity of the forced convection basal ablation model was assessed as the average percent increase in cumulative basal ablation predicted for the duration over which basal ablation was derived with each incremental increase in the value assigned to a given variable or parameter. The sensitivity was analyzed over this longer time period due to the certainty in the bulk basal ablation derived from total ice thinning and surface ablation.
3.3 Thinning (spatial assessment)
A repeat transect was conducted to assess spatial variation in thickness and thinning and to verify that the sIPR data were representative with respect to other locations across the ice island. An initial thickness profile was collected with a 25 MHz mIPR (Blue System Integration Ltd.) that was towed by snowmobile over an approximately 3 km transect on 8 May 2016. A series of 10 ablation stakes were also installed along the profile route. Thickness data were collected over 2.4 km of the original transect when the same mIPR system was towed on foot on 28 September 2016. Eight of the stakes were also remeasured at this time. Further details of the mIPR system can be found in S1 and Mingo and Flowers (2010).
All mIPR processing was conducted with Radar Tools (release 0.4), a library of Python scripts and tools that was used to standardize, clean, visualize, and process data contained in the raw radar data (S1; Wilson, 2013). This program was also used to select the location of the air and reflected radar waves. Ice thickness was calculated with Eq. (3) (Wilson, 2012):
where H is thickness (m), s is the distance between the transmitting and receiving antennas (m), t is the time (s) between the recording of the air and reflected waves by the receiver, and va is the speed of the electromagnetic wave in air (3.0×108 m s−1) travelling between the transmitter and receiver (Wilson, 2012). The speed of the radar wave in ice (v) was set to 1.7×108 m s−1 (Macheret et al., 1993). The ice thickness resolution (±0.5 m) was limited by v and the waveform sampling interval of the mIPR system (Crawford, 2013).
Snow was present on the ice surface when the mIPR transect was conducted in May 2016. An insufficient number of snow depth measurements were recorded to adequately account for the snow depth over the transect area, and it was not possible to distinguish the snow–ice interface in the radargram. Thickness (ice + snow) in May was therefore calculated using a single velocity value, m s−1. However, an additional uncertainty was added to the May ice thickness to account for the possible presence of snow. This uncertainty was based on the mean snow depth (36 cm) recorded at nine locations along the mIPR transect and the amount of time a radar wave would travel through this layer given that m s−1 for snow (Haas and Druckenmiller, 2009). The errors associated with the resolution of the mIPR system and the average snow depth estimate were summed to determine the average amount that the ice thickness, as measured in May, could be overestimated by (0.8 m). Uncertainty in thickness change calculations was determined by propagating the uncertainties in ice thickness resulting from the resolution of the mIPR system and the presence of snow.
The magnitude of thinning that occurred between May and September 2016 was calculated between the closest pairs of mIPR traces recorded during each field visit. To improve positional accuracy, the locations recorded by the mIPR onboard GPS were replaced with those recorded by a HiPer V dual-frequency GPS (Topcon Corp.) after precise point positioning (PPP) processing (Natural Resources Canada, 2016). The September transect was adjusted relative to the orientation of PII-A-1-f in May by matching mIPR traces known to be collected at the same location (i.e. the ablation stakes) on the ice island to correct for a small amount of movement by the ice island between the two field visits. Since it was not possible to retrace the transect exactly due to changes in topography between field visits, the thickness measurements that were compared between May and September were offset by varying distances (metres to tens of metres). Using Eq. (4), we derived an index of comparability for these measurements from the percentage of overlap between the radar footprints at the ice–water interface. The radii (r) of these footprints depend on the centre wavelength of the 25 MHz antenna (λ=6.8 m), relative permittivity of ice (K; 3), and H (Leucci et al., 2003),
The positions of thickness change measurements were categorized as ≥50 % overlap, ≥30 % overlap, <30 % overlap, and no overlap.
3.4 Surface extent reduction and contributions to deterioration
The areal extent of PII-A-1-f was monitored with seven RADARSAT-2 FQ SAR scenes to determine the relative importance of surface and basal ablation to the total deterioration of the ice island. The SAR scenes were acquired between 1 November 2015 and 23 September 2017, and the image processing and areal extent digitization details are included in S2. We quantified and compared the contributions of basal ablation, surface ablation, and areal reduction processes (e.g. fracture, forced and buoyant convection, wave erosion, and calving) to the overall deterioration of PII-A-1-f over the temporal-extent sIPR data collection. We also estimated the contribution of surface and basal ablation to total deterioration over the longer temporal extent in which RADARSAT-2 FQ images were acquired. For this estimation, a cubic spline was applied to fill missing cumulative ablation values between 24 September 2016 and 21 October 2016, and it was assumed that the same surface and basal ablation magnitudes that occurred in the first year of observation also occurred between October 2016 and September 2017.
4.1 Thinning (temporal assessment) and environmental conditions
PII-A-1-f decreased in thickness by 4.7±1.4 m over the 11 months that sIPR data were collected and by 4.0±1.4 m during the 10 months that basal ablation was estimated and used for the basal ablation model calibration (Fig. 3a; Table 1). The latter can be divided into three periods related to surface ablation magnitudes as per the ablation stake data (Fig. 3b; Table 1). These are referred to as “ablation periods” in the remainder of the text. Minimal surface ablation was observed over ablation period 1 (November to mid-December 2015). No surface ablation occurred during period 2, which distinguishes it from ablation periods 1 and 3. Therefore, basal ablation was the sole contributor to thinning during ablation period 2, when the mean daily thinning rate was 0.9 cm d−1 (mid-December 2015 to mid-July 2016). The thinning rate tripled during ablation period 3, which spanned from mid-July to September 2016, due to the onset of continuous surface ablation in mid-July. Ninety-eight percent of the recorded surface ablation occurred in this period, when Ta was consistently >0 ∘C. Ta was >0 ∘C for 15 % of the second ablation period; however, this contributed to melting the snow that had accumulated on the ice surface instead of ice ablation (Fig. 3b; Table 1).
Table 1Ablation and total thinning magnitudes and rates per ablation period. Air temperature (Ta) data for each period are also included. Inconsistencies exist between the summed ablation and thinning magnitudes or between the ratios of surface: basal ablation magnitudes versus rates are due to rounding. Ms and Mb (in italic font) represent daily surface and basal ablation rates, respectively.

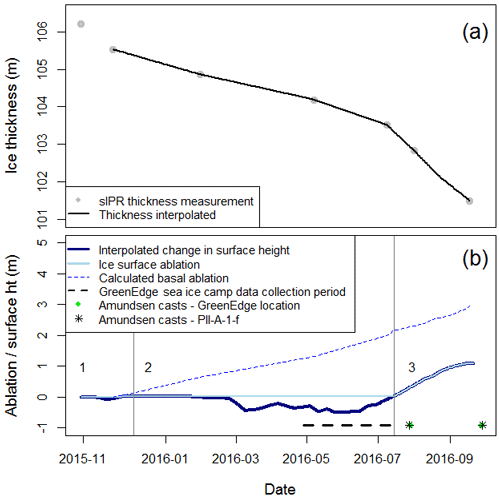
Figure 3Ablation and thickness change. (a) Thickness change of PII-A-1-f as measured by the stationary ice-penetrating radar (sIPR; grey dots) and interpolated between thickness measurements (black line). The first thickness observation was not included in the interpolation due to uncertainty imposed by sIPR measurement resolution. (b) Surface and basal ablation as well as the change in surface height (ht) relative to the start of sIPR data collection. The latter, represented by the thick blue line, includes ice ablation (positive values) as well as snow accumulation (negative values). Basal ablation is calculated with the linearly interpolated thickness values in (a) and should be taken as an estimate of daily magnitudes. The vertical lines denote three surface ablation periods described in Table 1. The timing of CTD profiling by the CCGS Amundsen and the time span associated with oceanographic data collection at the GreenEdge sea ice camp are also denoted.
The mean daily basal melt rate (Mb) between November 2015 and September 2016 was almost 3 times greater than the mean rate of daily surface ablation (Ms; cm d−1). However, this ratio varied between ablation periods. For example, the mean Mb was 7 times greater than the mean Ms during ablation period 1, when only 2 cm of surface ablation was observed. In contrast, the mean Ms was approximately 50 % greater than the mean Mb over ablation period 3, when over 1 m of surface ablation was observed over the 2-month duration (Fig. 3b; Table 1). The mean Mb increased between successive ablation periods (Table 1), and the increase in daily mean Mb from 0.9 to 1.2 cm d−1 between periods 2 and 3 coincides with an increase in CMEMS temperature and velocity. The mean Mb increased between successive ablation periods (Table 1), and the increase in daily mean Mb from 0.9 to 1.2 cm d−1 between periods 2 and 3 coincides with an increase in CMEMS temperature and velocity.
4.2 Basal ablation model calibration
4.2.1 Oceanographic data comparisons
Figure 4 shows the CMEMS Θ, SA, and u for the duration that PII-A-1-f basal ablation was derived. The mean Θ and SA of measurements from CTD casts acquired in the vicinity of PII-A-1-f or the GreenEdge sea ice camp are plotted alongside the model data in Fig. 4a and b. These data are associated with the depth interval of the model data that the keel of the ice island fell within for the duration of the data collection. The mean u in this depth interval, as measured by the ADCP moored near to the GreenEdge sea ice camp location, is included in Fig. 4c. The data collected at the GreenEdge sea ice camp (Θ and SA) and at the nearby moored ADCP (u) provide the longest in situ time series of oceanographic conditions and were used to assess if these variables were consistently over- or underestimated in the CMEMS data.
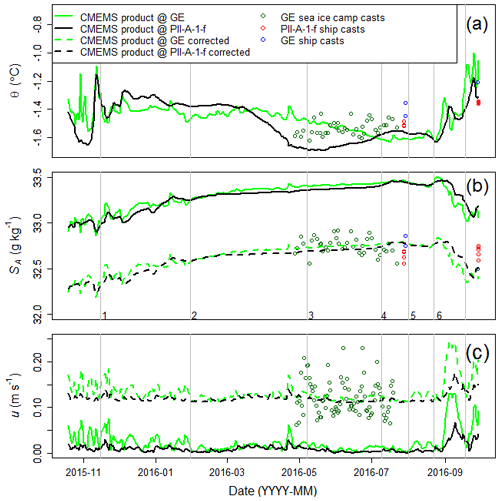
Figure 4Oceanographic data collected or modelled over the time span that PII-A-1-f basal ablation rates were derived. CMEMS product data for the grid cells in which PII-A-1-f (solid black lines) and the GreenEdge sea ice camp (solid green lines) were located: (a) conservative temperature (Θ), (b) absolute salinity (SA), and (c) velocity (u). As PII-A-1-f was grounded, u is equivalent to the differential velocity between the ice island and the ocean current. Field data collected by the CCGS Amundsen and the GreenEdge project are shown in the respective panels. The CMEMS data, corrected for bias in SA and u, are shown as dotted lines in (b) and (c), respectively. The vertical lines denote the calibration intervals, numbered in (b), associated with thickness change measurements that were used for the calibration of the forced convection basal melt model. Generated using EU Copernicus Marine Service information.
The means of the absolute daily difference between Θ and SA at the GreenEdge sea ice camp and the CMEMS data were 0.07 ∘C and 0.67 g kg−1, respectively. The CMEMS SA was consistently greater than the in situ data and was therefore corrected by subtracting 0.67 g kg−1 (Fig. 4b, dotted lines). A bias in Θ was not seen, and no correction was applied; however, there was a consistent underestimation of u in the CMEMS data (Fig. 4c). The CMEMS data were corrected by the mean daily difference (0.1 m s−1) between the CMEMS and in situ values of u (Fig. 4c, dotted lines).
CTD profiles collected in the vicinity of PII-A-1-f and the GreenEdge sea ice camp on successive days by the CCGS Amundsen in July and September 2016 were plotted (not shown) to compare the oceanographic conditions at the two sites. In the depth interval of interest, the values of Θ and SA were reasonably similar and not consistently different between sites. This supported our use of the SA correction for the CMEMS data that were derived from the difference between the CMEMS data and the longer time series collected at the GreenEdge sea ice camp. This SA correction was applied to the CMEMS data associated with the location of PII-A-1-f, which was used for the model calibration (Fig. 4b).
The full CMEMS Θ and SA profiles were also plotted (not shown) against those acquired by the CCGS Amundsen to ensure that the CMEMS data were generally representative of the water column. The CMEMS profiles were reasonable in form, and, in the depth interval of interest, CMEMS consistently overestimated the SA recorded by the CTD casts acquired by the CCGS Amundsen. The average overestimation was 0.60 g kg−1. This further supports the decision to apply the 0.67 g kg−1 correction to the CMEMS SA for the forced convection basal ablation model calibration. The CMEMS Θ was both over- and underestimated in the depth interval of interest, which confirms that not applying a correction to this variable was appropriate.
4.2.2 Model calibration and sensitivity analysis
Ci values were calculated with the uncorrected and corrected CMEMS data for each of the six calibration intervals. The range and mean values of Ci calculated with the uncorrected CMEMS data were an order of magnitude larger than those that were theoretically derived by Weeks and Campbell (1973; m2∕5 s ∘C−1) and White et al. (1980; m2∕5 s ∘C−1). Due to this, plus the poor representation of uncorrected CMEMS SA and u, it was decided to further analyze the more reasonable Ci values that were calculated with the corrected CMEMS data. These latter values of Ci are included in Table 2 with the corresponding mean ΔT and u values found with the CMEMS data.
Table 2Calibrated values for Ci for the individual calibration intervals associated with each measured change in ice thickness. The corresponding mean driving temperature (ΔT) and velocity (u) values, found with the CMEMS data, are also provided.
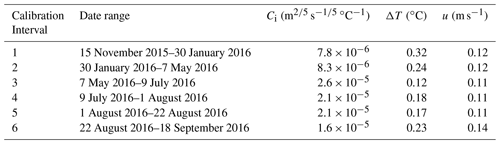
Using these data, the mean Ci value was 1.7×10−5 m2∕5 s ∘C−1, and values for the individual calibration intervals ranged from to m2∕5 s ∘C−1. The greatest values of Ci were associated with calibration intervals 3 through 6. Cumulative basal ablation was over-predicted by 38 % when the forced convection basal ablation model was run with the mean Ci value over the 308 d that basal ablation was calculated. Finally, when calculated with the total basal ablation and total driving force between 15 November 2015 and 18 September 2016, C was calibrated to m2∕5 s ∘C−1.
Values of u, Θ, and L were not normally distributed. Therefore, the median values of these variables were first assigned during the sensitivity analysis when a given variable was held constant. The calibrated Ci values were found to follow a normal distribution, though the power of this test is low due to the small sample size. For consistency, the median Ci value was also assigned when this parameter was held constant during the sensitivity analysis.
Of the environmental driving variables included in the forced convection basal ablation model, ΔT had the greatest relative range of values over all of the calibration intervals (0.10 to 0.37 ∘C). A mean increase of 19 % was applied to the ΔT value during the sensitivity analysis, and the same increase in cumulative basal ablation was predicted over the time period that basal ablation was derived with observations. This is due to the linear relationship between ΔT and Mb in Eq. (1) (Table 3).
Table 3Descriptive statistics and sensitivity analysis results. The key driving variables in the forced convection basal ablation model were individually perturbed in eight equal increments based on the variable's range. The sensitivity of the model was assessed as the mean percent increase in predicted cumulative basal ablation following each incremental increase in the value assigned to a given variable. The sensitivity was analyzed over the longer time period (15 November 2015 to 18 September 2016) due to the certainty in the bulk basal ablation.

A linear relationship also exists between C and Mb in Eq. (1); however, the range in Ci was more constrained relative to the ΔT data series. For this reason, the cumulative predicted basal ablation only increased by 16.5 % with each incremental change in the value assigned to C during the sensitivity analysis (Table 3). Finally, due to the smaller range of u (0.11 to 0.18 m s−1) and the non-linear relationship between u and Mb in Eq. (1), the relative increment adjustment (6.1 %) and corresponding change (4.8 %) to the predicted cumulative basal ablation over the time period that basal ablation was derived with observations was less than that associated with ΔT or C.
4.3 Thinning (spatial assessment)
The data collected at the main site on PII-A-1-f over 11 months provide unprecedented information regarding the temporal thinning of an ice island. However, these data are representative of a single point on a large ice island. Considering that the rate of surface ablation along the mIPR transect would have been near zero until the snow had melted around 15 July 2016, as determined from the ablation stakes at the sIPR site, the surface would have ablated at a rate of 1.5 cm d−1 after this date. This is slightly less than the rate at the sIPR site over ablation period 3 (1.6 cm d−1; Table 1) and increases the confidence that the surface ablation conditions at the sIPR site were similar to those across the mIPR transect.
The ice island thickness over the mIPR transect ranged from 80.7 to 127.1 [−0.5, +0.8] m in May and 77.3 to 123.7±0.5 m in September 2016 (Fig. 5a). A 50 m long section of relatively thin ice that was approximately 80 m thick was recorded along transect segment AB during both field visits (Fig. 5a); this section was approximately 40 m thinner than adjacent areas. The air and basal wave locations in the mIPR data could not be definitively selected when this thin section was passed during transect segment CD (Fig. 5a). This made it impossible to ascertain thickness at this location; however, a pair of in-line hyperbolae in both the May and September 2016 radargrams support the interpretation that this thinner section ran across both transect segments AB and CD. This section of thin ice is referred to as a “subsurface feature” and corresponds to the location of the linear “surface feature” described in Sect. 2. Together these are referred to as the “paired feature”.
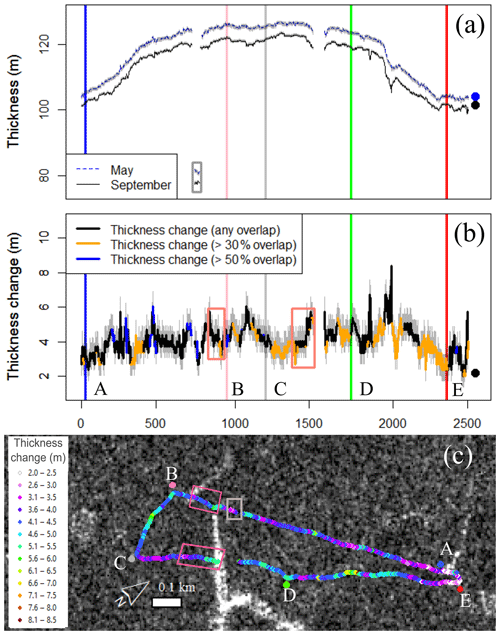
Figure 5Spatial variation in morphology and thinning between May and September 2016. Upper-case letters are used to denote transect segments referred to in the text. (a) Thickness observations collected with mobile ice-penetrating radar. The grey box corresponds with the thin ice section also denoted in (c). (b) Thickness change. The pink boxes indicate thickness change gradients also identified in (c). Thinning data were categorized based on the amount of overlap between the May and September radar footprints. Grey shading in (a) and (b) denotes uncertainty in thickness measurements and thinning amounts, respectively. The larger, single points denote the respective thickness and thinning measured with corresponding data collected by the sIPR at the main site. (c) Thickness change displayed on a Fine Quad RADARSAT-2 synthetic aperture radar scene acquired on 28 September 2016 (shown in greyscale). A surface feature is apparent as a line of high-backscatter (white) pixels starting at the sidewall notch. The geolocation error of the RADARSAT-2 scene was evaluated, and minimal error in the position of the scene was observed.
The magnitude of thinning (3 to 4 m) observed over this thin section present along transect segment AB (shown in the grey boxes in Fig. 5) was in the low to middle range of the thinning observed along the entire transect. However, the general gradient in thinning magnitudes leading to the paired feature shows a similar pattern in both transect segments AB and CD (shown in the pink boxes in Fig. 5). Thinning magnitudes of 3 to 4 m increased to 5 to 6 m across a distance of approximately 90 to 150 m, ending at the surface feature and where a gap in the thickness record exists. A fracture that occurred along this paired feature in September 2017 caused the areal extent of the ice island to reduce by approximately 2.7±0.1 km2.
4.4 Volume and area loss and contributions to deterioration
The area and volume of PII-A-1-f were 13.2±0.01 km2 and 1.4±0.01 km3, respectively, when it was first visited in October 2015. By September 2016, the volume and areal extent decreased by 0.4±0.01 km3 and 3.4±0.1 km2, respectively. A fracture event in September 2016 caused approximately 94 % of the areal reduction and 88 % of this volume loss. These values represent the maximum possible reductions caused by the fracture. Other areal reduction processes (e.g. small-scale calving) would also have contributed to areal reduction during the time interval between RADARSAT-2 acquisitions over which the fracture occurred.
The 23-month RADARSAT-2 monitoring period (October 2015 to September 2017) captured a longer period of areal change. During the latter half of this time span (i.e. September 2016 and September 2017), the ice island un-grounded and re-grounded twice in the same vicinity, and the large September 2017 fracture event occurred (Fig. 1e). The ice island volume decreased by 0.6±0.01 km3 over this period, with the vast majority of this volume loss (94 %) being caused by processes that decreased the areal extent of the ice island. The remaining volume was lost to basal and surface ablation, with basal ablation causing 3 times more volume loss than surface ablation. These ablation magnitudes were extrapolated from the on-ice data collection period. Over the entire 2 years that PII-A-1-f was monitored via RADARSAT-2 image acquisition, areal reduction processes reduced the volume of the ice island by approximately 67 %. Combined, surface and basal ablation resulted in an approximate 7 % reduction of the ice island volume, with basal ablation again causing 3 times more loss than surface ablation.
5.1 Basal ablation model calibrations
Two approaches are predominately used to model ice island and iceberg basal ablation (Bouhier et al., 2018). The first is the semi-empirical fluid-dynamics approach that is calibrated in this study; Eq. (1) approximates melt resulting from the bulk energy transfer occurring within the complex boundary conditions that are present at the ice–water interface (Weeks and Campbell, 1973; White et al., 1980). This model has been widely utilized for iceberg and ice island basal ablation modelling in both the Arctic (Ballicater Consulting, 2012; Bigg et al., 1997; Keghouche et al., 2010; Wagner and Eisenman, 2017) and Antarctic (Gladstone et al., 2001; Martin and Adcroft, 2010; Merino et al., 2016). The second approach is based on thermodynamic principles (Bouhier et al., 2018). Holland and Jenkins (1999) and Hellmer and Obers (1989) document a more complex three-equation thermodynamic model for ice shelf basal ablation, which represents both the salt and temperature flux across the ice–ocean interface.
The forced convection basal ablation model is advantageous due to its computational simplicity and the direct incorporation of Δu. In the thermodynamic approach, the values assigned to the turbulent heat and salt exchange parameters must be adjusted for varying values of Δu in iceberg and ice island applications (Jansen et al., 2007). Jansen et al. (2007) provide calibrated values for three stages of drift, each with a unique range of Δu values for an Antarctic ice island, while Eq. (1) in the forced convection model directly incorporates Δu. Equation (2) was developed to account for the plume of relatively cold and fresh iceberg meltwater that has been observed to surround icebergs and inhibit further melt (Foldvik et al., 1980). This meltwater plume will be stripped from the keel as Δu increases, as is the case when an ice island is grounded (Jansen et al., 2007). Therefore, different parameterizations of Eq. (2) are likely required for predicting the basal ablation of drifting versus grounded ice islands, which FitzMaurice et al. (2017) showed to be the case when parameterizing Eq. (1) for the sidewall melt of an iceberg with different scenarios of meltwater plume and relative ocean velocities. It is possible that an adjustment to the melting point of ice (Mp) to account for the influence of the meltwater plume is not necessary under some conditions, and Mp will simply equal the far-field ocean freezing temperature (Θf). Determining this will require concerted study of the difference in the basal boundary layer conditions of grounded versus drifting ice islands. The Δu for a drifting iceberg or ice island will be influenced by both ocean and wind currents (Kubat et al., 2005; Lichey and Hellmer, 2001). Observations of Δu for the drifting ice island case are rare but would be useful for this work and for correctly assigning values to this variable in Eq. (1).
This study used a unique dataset of observed ice island thinning as well as in situ and modelled oceanographic conditions to present a calibration of the forced convection basal ablation model. It is noted that the exponents within Eq. (1), which were derived for the flat plate nature of a tabular iceberg or ice island, could also be calibrated. However, these have remained constant in previous iceberg and ice island literature, while the bulk heat transfer coefficient, C, has typically been assigned one of two values that differ by an order of magnitude. Bigg et al. (1997), Bouhier et al. (2018), Martin and Adcroft (2010), Wagner and Eisenman (2017), and Weeks and Campbell (1973) assign a value of m2∕5 s ∘C−1. However, the confidence interval of the normal distribution of our calibrated C values does not overlap with this theoretically derived value of the bulk heat transfer coefficient. We recommend assigning the C parameter a value of m2∕5 s ∘C−1 when modelling ice island basal ablation in the future. This value was calculated from the calibration conducted over the full time span that basal ablation data were available and not the individual calibration intervals associated with the measured changes in ice thickness. In addition, the confidence interval of the normal distribution of Ci values found in Table 2 does overlap with this value. The value also matches, remarkably, that which was theoretically derived by White et al. (1980) and was assigned in the ice island deterioration model used by the CIS (Ballicater Consulting, 2012). We believe that it is more appropriate to use this value instead of the mean of the individually calibrated Ci values reported in Table 2 ( m2∕5 s ∘C−1), as we cannot be sure of the alignment between changes in oceanographic conditions, basal melt rates, and Ci values due to the low resolution of data collected by the sIPR. It is noted that Crawford et al. (2018b) assigned a value of m2∕5 s ∘C−1 to C, supplied by Crawford (2018), when quantifying the distribution of freshwater input from ice island melt through the eastern Canadian Arctic. The use of this previous value would cause very minimal skew in the distribution of freshwater input, slightly overestimating the freshwater input at the higher latitudes in their study region.
The calibration of the bulk heat transfer coefficient (C) is specific to the approach used to assign an ice temperature when deriving the driving temperature, ΔT. This paper follows the approach of Weeks and Campbell (1973), White et al. (1980), Løset (1993a), Kubat et al. (2005), and Ballicater Consulting (2012), empirically estimating the ice interface temperature (Eq. 2) based on work by Josberger (1977). This contrasts with a line of successive papers (e.g. Bigg et al., 1997; Martin and Adcroft, 2010; FitzMaurice et al., 2016; Wagner and Eisenman, 2017) that assign a constant ice temperature (Tice) of −4 ∘C based on Løset (1993b). This study reported temperature measurements at ∼50 cm depth of several iceberg sails in the Barents Sea and show that this temperature will be reached within a few metres of the ice–ocean interface using a model (Løset 1993b). Yet another paper assigns ∘C for sidewall melt calculations (FitzMaurice et al., 2017). These discrepancies underscore the need for harmonization on how Tice is derived or assigned in the context of the forced convection basal ablation model. We recommend that the melting point of ice be assigned to Tice in future studies that use this model, as it is the actual temperature of the ice–water interface, easy to calculate, and physically meaningful. Our recommendation is also supported by the model comparison and sensitivity study of FitzMaurice and Stern (2018); this work found that the thermodynamic and forced convection models agree when Tice=Mp and infer that the heat flux into the iceberg interior is small. For the sake of inter-comparison, example calculations using L, SA, Θ, and u values representative of conditions at PII-A-1-f, the calibrated value of C would decrease by 1 order of magnitude if ∘C. The calibrated C value would then be in line with that derived by Weeks and Campbell (1973). The value of C would decrease by 2 orders of magnitude if −15 ∘C were assigned to Tice.
The in situ dataset of oceanographic conditions in the vicinity of PII-A-1-f and the GreenEdge sea ice camp was of paramount importance for validating and correcting the CMEMS data for bias. However, the calibration could be further improved by obtaining a longer time series of oceanographic data in closer proximity to the ice island. In general, there is a paucity of in situ oceanographic data collected in the vicinity of ice islands. Collection of such data will allow for further improved drift and deterioration analyses of icebergs and ice islands. Modifying the sIPR to resolve smaller magnitudes of thickness change is also recommended. This would make it possible to relate these higher-quality thinning measurements to corresponding surface ablation and recorded oceanographic conditions.
5.2 Ablation rates and contributions to overall deterioration
Field measurements of ice island thinning are extremely sparse. Scambos et al. (2008) installed numerous instruments on two Antarctic tabular icebergs while investigating their deterioration processes with field and remote-sensing data. Unfortunately, it was impossible to process thickness measurements collected by a radio-echo sounder installed on one of the icebergs (Scambos et al., 2008). Prior to our study, the spot values reported by Halliday et al. (2012) from a 17 km2 ice island drifting in the Labrador Sea were the only known field observations of ice island thinning. The PII-A-1-f thinning dataset greatly improves on this previous work, as the long-term sIPR time series and repeat mIPR transects together produce a comprehensive dataset that allows us to assess the spatial and temporal variations in thinning and ablation. It would be highly beneficial to redeploy the sIPR on a drifting ice island in the future to (1) augment the number of observations of ice island thinning and (2) begin comparing basal ablation occurring to drifting versus grounded ice islands.
The average Mb of 3.4 cm d−1 reported by Halliday et al. (2012) was greater than that observed for PII-A-1-f. Since the basal ablation rate for a drifting ice island should be lower than that of a grounded ice island due to decreased Δu and the potential protection of a meltwater plume, this greater melt rate was likely due to the higher Θ off the coast of Labrador. Elevated ocean temperatures also contributed to the high, 13.5 m month−1 basal ablation rate that Jansen et al. (2007) estimated for the grounded Antarctic ice island “A38-B”. Basal ablation was reported to cause 96 % of the thinning of this ice island that had a surface extent of approximately 7600 km2 (Jansen et al., 2007), whereas 73 % of the thinning of PII-A-1-f was a result of this process. We note that, when present, the densification of firn is a factor in the surface ablation of Antarctic tabular icebergs. Scambos et al. (2008) document firn characteristics on two Antarctic tabular icebergs, and a follow-up field study that combines such observations with repeated thickness measurements would be valuable for assessing the contributions of surface and basal processes to Antarctic iceberg thinning.
While basal ablation was responsible for the majority of the thinning of PII-A-1-f, this process caused the ice island volume to reduce by approximately 5 %. However, basal ablation indirectly influences further deterioration by reducing the relative thickness of the ice island and decreasing fracture resistance (Goodman et al., 1980; Jansen et al., 2005). This will happen more quickly if an ice island is grounded, as basal ablation could increase by a factor of 2 after an ice island stops drifting freely (Jansen et al., 2007). Future research, including finite-element modelling (e.g. Sazidy et al., 2019), is warranted to assess if and how thinning contributed to the September 2017 calving event. This fracture occurred along the paired feature that was substantially thinner than adjacent ice surfaces and which emanated from the root of the sidewall notch. We also recommend that further research be conducted into the relationship between the presence of the paired feature, the propagation of the sidewall notches before and during the time that PII-A-1-f was grounded in southern Baffin Bay, and the ultimate September 2017 fracture. The enlargement of sidewall notches, similarly to cusped deterioration patterns observed by Ballicater Consulting (2012), is a recurring deterioration mechanism that is not considered in deterioration studies or models at this point in time.
This study focuses on the thinning of PII-A-1-f, an ice island that originated from a calving event at the Petermann Glacier in 2012 and was grounded in western Baffin Bay over a 2-year monitoring time span. A unique field dataset was collected over four visits between October 2015 and September 2016 and was used to report ice island thinning and ablation rates and calibrate the popular forced convection basal ablation model.
The time series of ice island thinning recorded with a customized sIPR showed that the ice island thinned by 4.7 m over the 11 months that on-ice data were collected. Basal ablation was responsible for 73 % of the observed thinning. Overall, PII-A-1-f was likely more susceptible to fracture than if it had been freely drifting, due to enhanced basal ablation and a correspondingly faster reduction in relative thickness.
It is important to model ice island basal ablation accurately for predicting the impact of meltwater input on the ocean system (Crawford et al., 2018b; Jansen et al., 2007). Additionally, basal ablation will alter the relative thickness of an ice island, which will influence fracture likelihood (Goodman et al., 1980), drift patterns (Barker et al., 2004), and grounding locations (Sackinger et al., 1991). This is the first study to calibrate the forced convection basal ablation model for ice island or iceberg use with field data of ice island thinning, which removed uncertainty regarding estimated ablation rates from remotely sensed datasets. The calibrated value of the bulk heat transfer coefficient ( m2∕5 s ∘C−1) is in line with the larger of two values assigned in previous iceberg and ice island basal ablation models, and we recommend that this value, specific to our approach of deriving a driving temperature, be used in future modelling endeavours. It is important to conduct such field studies to develop and validate methods for modelling ice island thickness change (i.e. surface and basal ablation), as this will inform future deterioration investigations and improve ice island drift and deterioration forecasting in both of the polar regions (Barker et al., 2004). The calibration of the forced convection basal ablation model might also be used to generally predict when grounded ice islands might thin enough to drift free, assuming certain shoal bathymetry and ice island morphology. This may be especially useful along the eastern coast of Canada, where shipping and offshore industry operates and where ice island grounding is a common occurrence. Overall, the work presented in this study highlights the value of systematic ice island field data collection. This is necessary for deterioration analyses, connecting morphology and deterioration, and developing high-quality models for operational and research purposes.
Amundsen CTD data are available from the Polar Data Catalogue (PDC) (https://doi.org/10.5884/12713, Amundsen Science Data Collection, 2019). Data collected at PII-A-1-f by the authors (i.e. data associated with ablation stakes, the weather station and sonic ranger, and sIPR and mIPR) are also available from PDC (https://doi.org/10.21963/13091, Mueller et al., 2019), as are the RADARSAT-2 imagery (GeoTIFFs) and digitized polygons of the areal extent of PII-A-1-f. This study has been conducted using EU Copernicus Marine Service information. CMEMS products are available at http://marine.copernicus.eu/services-portfolio/access-to-products/ (last access: March 2020). Data associated with the GreenEdge project are available, either through download or correspondence with a project coordinator, at http://www.greenedgeproject.info/data.php (GreenEdge, 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/tc-14-1067-2020-supplement.
AJC, GC, and DM were responsible for project design. LM designed and produced the stationary and mobile ice-penetrating radars and assisted in data processing and interpretation. AJC carried out fieldwork and data analyses. DD and MB provided oceanographic data associated with the GreenEdge sea ice camp. DM, GC, LD, LM, and DD contributed to the preparation of the paper, which was led by AJC.
The authors declare that they have no conflict of interest.
We would like to acknowledge the field assistance of Jaypootie Moesesie, Graham Clark, Jill Rajewicz, Jonathan Gagnon, Luke Copland, Abigail Dalton, Lauren Candlish, Hugo Jacques, Tom Desmeules, Natalie Theriault, Alison Cook, Alexis Burt, Leah Braithwaite, Julie Payette, Claire Bernard-Grand'Maison, Eric Brossier, and Christian Haas. Adam Garbo and Iain Burnett helped with field preparation. This unique dataset would not be possible to collect without the access provided through the collaboration of ArcticNet and the CCGS Amundsen. We thank the Canadian Coast Guard (CCG) captains Alain Lacerte and Alain Gariépy as well as Transport Canada pilots Olivier Talbot, Alain Roy, and Guillaume Carpentier for providing safe transport to our field site. We also greatly thank the entire CCG crew, who were instrumental in our field success. The hard work of ArcticNet staff, including Keith Lévesque, Phillipe Archambault, Louis Fortier, Jean-Éric Tremblay, Tim Papakyriakou, Leah Braithwaite, Annisa Merzouk, and Colleen Gombault deserves great recognition. We thank Doug King, Geography and Environmental Studies, Carleton University, Shawn Kenny, Civil and Environmental Engineering, Carleton University, Douglas MacAyeal, University of Chicago, and two anonymous referees for reviewing an earlier version of the paper.
This study has been conducted using EU Copernicus Marine Service Information. RADARSAT-2 scenes were acquired through a joint partnership agreement between the Water and Ice Research Lab and the Canadian Ice Service, Environment and Climate Change Canada. RADARSAT data and products are © MacDonald, Dettwiler and Associates Ltd. (2010–2017), all rights reserved. RADARSAT is an official mark of the Canadian Space Agency. Some of the data presented herein were collected by the Canadian research icebreaker CCGS Amundsen and made available by the Amundsen Science program, which was supported by the Canada Foundation for Innovation and Natural Sciences and Engineering Research Council of Canada. The views expressed in this publication do not necessarily represent the views of Amundsen Science or those of its partners. Some of the data presented in this analysis were collected by the GreenEdge project. The GreenEdge project is funded by the following French and Canadian programs and agencies: ANR (contract no. 111112), CNES (project no. 131425), IPEV (project no. 1164), CSA, Fondation Total, ArcticNet, LEFE, and the French Arctic Initiative (GreenEdge project). The GreenEdge project would not have been possible without the support of the hamlet of Qikiqtarjuaq and the members of the community as well as the Inuksuit School and its principal, Jacqueline Arsenault. The GreenEdge project is conducted under the scientific coordination of the Canada Excellence Research Chair in Remote Sensing of Canada's New Arctic Frontier and the CNRS and Université Laval Takuvik Joint International Laboratory (UMI3376). The GreenEdge field campaign was successful thanks to the contribution of Joannie Ferland, Guislain Bécu, Claudie Marec, José Lagunas, Flavienne Bruyant, Jade Larivière, Eric Rehm, Simon Lambert-Girard, Cyril Aubry, Catherine Lalande, Anita LeBaron, Constance Marty, Julie Sansoulet, Debbie Christiansen-Stowe, Andrew Wells, Maxime Benoît-Gagné, Emmanuel Devred, and Marie-Hélène Forget from the Takuvik laboratory; Christopher-John Mundy and Virgine Galindo from the University of Manitoba; and Frace Pinczon du Sel and Eric Brossier from Vagabond. The GreenEdge project also thanks Michel Gosselin, Québec-Océan, the CCGS Amundsen, and the Polar Continental Shelf Program for their in-kind contribution in polar logistic and scientific equipment.
Instrument development and fieldwork were supported by the Northern Transportation Adaptation Initiative of Transport Canada, the Polar Knowledge Canada Safe Passage project (no. 1516-065), and Polar Knowledge Canada's Northern Scientific Training Program. Anna J. Crawford received personal funding from the Garfield Weston Foundation, the Natural Sciences and Engineering Research Council (Canada), and Environment and Climate Change Canada.
This paper was edited by Dirk Notz and reviewed by two anonymous referees.
Abramoff, M. D., Magalhaes, P. J., and Ram, S. J.: Image processing with ImageJ, Biophotonics Int., 11, 36–42, 2004.
Amundsen Science Data Collection: CTD data collected by the CCGS Amundsen in the Canadian Arctic, Processed data, Version 3, Archived at https://www.polardata.ca/, last access: 18 October 2016.
Amundsen Science Data Collection: CTD data collected by the CCGS Amundsen in the Canadian Arctic. ArcticNet Inc., Québec, Canada, Processed data, Version 1, Canadian Cryospheric Information Network (CCIN), Waterloo, Canada, https://doi.org/10.5884/12713, 2019.
Ballicater Consulting: Ice Island and Iceberg Studies 2012, Canadian Ice Service, Environment Can., Ottawa, Ont., Contract Report, 73 pp., 2012.
Barker, A., Sayed, M., and Carrieres, T.: Determination of iceberg draft, mass and cross-sectional areas, in: Proceedings of the 14th International Offshore and Polar Engineering Conference, Toulon, France, 23–28 May 2004, 1–6, 2004.
Bigg, G. R., Wadley, M. R., Stevens, D. P., and Johnson, J. A.: Modelling the dynamics and thermodynamics of icebergs, Cold Reg. Sci. Tech., 26, 113–135, 1997.
Bouhier, N., Tournadre, J., Rémy, F., and Gourves-Cousin, R.: Melting and fragmentation laws from the evolution of two large Southern Ocean icebergs estimated from satellite data, The Cryosphere, 12, 2267–2285, https://doi.org/10.5194/tc-12-2267-2018, 2018.
Crawford, A. J.: Ice island deterioration in the Canadian Arctic: Rates, patterns and model evaluation, MSc thesis, Department of Geography and Environmental Studies, Carleton University, Ottawa, Ont, Canada, 140 pp., https://doi.org/10.22215/etd/2013-10024, 2013.
Crawford, A. J.: Ice island deterioration, PhD dissertation, Department of Geography and Environmental Studies, Carleton University, Ottawa, Ont, Canada, 205 pp., https://doi.org/10.22215/etd/2018-13178, 2018.
Crawford, A., Crocker, G., Mueller, D., Desjardins, L., Saper, R., and Carrieres, T.: The Canadian Ice Island Drift, Deterioration and Detection (CI2D3) Database, J. Glaciol., 64, 517–521, https://doi.org/10.1017/jog.2018.36, 2018a.
Crawford, A., Mueller, D., Desjardins, L., and Meyers, P.: The aftermath of Petermann Glacier calving events (2008–2012): Ice island size distributions and meltwater dispersal, J. Geophys. Res., 123, 8812–8827, https://doi.org/10.1029/2018JC014388, 2018b.
Crawford, A., Mueller, D., and Joyal, G.: Surveying drifting icebergs and ice islands: Deterioration detection and mass estimation with aerial photogrammetry and laser scanning, Remote Sens., 10, 575, https://doi.org/10.3390/rs10040575, 2018c.
Dowdeswell, J. A. and Bamber, J. L: Keel depths of modern Antarctic icebergs and implications for sea-floor scouring in the geological record, Mar. Geol., 243, 120–130, https://doi.org/10.1016/j.margeo.2007.04.008, 2007.
FitzMaurice, A. and Stern, A.: Parameterizing the basal melt of tabular icebergs, Ocean Modelling, 130, 66–78, https://doi.org/10.1016/j.ocemod.2018.08.005, 2018.
FitzMaurice, A., Straneo, F., Cenedese, C., and Andres, M.: Effect of a sheared flow on iceberg motion and melting, Geophys. Res. Lett., 43, 12520–12527, https://doi.org/10.1002/2016GL071602, 2016.
FitzMaurice, A., Cenedese, C., and Straneo, F.: Nonlinear response of iceberg side melting to ocean currents, Geophys. Res. Lett., 44, 5637–5644, https://doi.org/10.1002/2017GL073585, 2017.
Foldvik, A., Gammelsrød, T., and Gjessing, Y.: Measurements of the radiation temperature of Antarctic icebergs and the surrounding surface water, Ann. Glaciol., 1, 19–22, https://doi.org/10.3189/S026030550001689X, 1980.
Fraser, A. D., Massom, R. A., Michael, K. J., Galton-Fenzi, B. K., and Lieser, J. L.: East Antarctic landfast sea ice distribution and variability, 2000–2008, J. Climate, 25, 1137–1156, https://doi.org/10.1175/JCLI-D-10-05032.1, 2012.
Fuglem, M. and Jordaan, I.: Risk analysis and hazards of ice islands, in: Arctic Ice Shelves and Ice Islands, edited by: Copland, L. and Mueller, D., Springer Netherlands, Dordrecht, 395–415, 2017.
Gladstone, R. M., Bigg, G. R., and Nicholls, K. W.: Iceberg trajectory modeling and meltwater injection in the Southern Ocean, J. Geophys. Res., 106, 19903–19915, 2001.
Goodman, D. J., Wadhams, P., and Squire, V. A.: The flexural response of a tabular ice island to ocean swell, Ann. Glaciol., 1, 23–27, 1980.
GreenEdge: GreenEdge data, available at: http://www.greenedgeproject.info/data.php, last access: March 2020.
Haas, C. and Druckenmiller, M.: Ice thickness and roughness measurements, in: Field Techniques for Sea Ice Research, edited by: Eicken, H., Gradinger, R., Salganek, M., Shirasawa, K., Perovich, D., and Leppäranta, M., University of Alaska Press, Fairbanks, Alaska, USA, 49–117, 2009.
Halliday, E. J., King, T., Bobby, P., Copland, L., and Mueller, D. R.: Petermann Ice Island `A' survey results, offshore Labrador, Proceedings of the Arctic Technology Conference, Houston, Texas, USA, 3–5 December 2012, OTC 23714, 2012.
Hellmer, H. H. and Olbers, D. J.: A two-dimensional model for the thermohaline circulation under an ice shelf, Antarctic Sci., 1, 325–336, https://doi.org/10.1017/S0954102089000490, 1989.
Higgins, A. K.: North Greenland ice islands, Polar Rec., 25, 207–212, 1989.
Holland, D. M. and Jenkins, A.: Modeling thermodynamic ice-ocean interactions at the base of an ice shelf, J. Phys. Oceanogr., 29, 1787–1800, 1999.
IOC, SCOR, and IAPSO: The international thermodynamic equation of seawater – 2010: Calculation and use of thermodynamic properties, Manuals and Guides No. 56, Intergovernmental Oceanographic Commission, UNESCO, Paris, France, 196 pp., 2010.
Jansen, D., Sandhager, H., and Rack, W.: Model experiments on large tabular iceberg evolution: ablation and strain thinning, J. Glaciol., 51, 1–11, 2005.
Jansen, D., Schodlok, M., and Rack, W.: Basal melting of A-38B: A physical model constrained by satellite observations, Remote Sens. Environ., 111, 195–203, https://doi.org/10.1016/j.rse.2007.03.022, 2007.
Josberger, E. G.: A laboratory and field study of iceberg deterioration, in: Proceedings of the First International Conference on Iceberg Utilization for Fresh Water Production, Weather Modification and other Applications, edited by: Husseiny, A. A., IA. Pergamon Press, New York, 245–264, 1977.
Keghouche, I., Counillon, F., and Bertino, L.: Modeling dynamics and thermodynamics of icebergs in the Barents Sea from 1987 to 2005, J. Geophys. Res., 115, C12062, https://doi.org/10.1029/2010JC006165, 2010.
Kelly, D.: gsw: Gibbs Sea Water Functions (v. 1.0-5), R package, 2017.
Kubat, I., Sayed, M., Savage, S. B., and Carrieres, T.: An operational model of iceberg drift, Int. J. Offshore Polar Eng., 15, 125–131, 2005.
Kubat, I., Sayed, M., Savage, S. B., Carrieres, T., and Crocker, G.: An operational iceberg deterioration model, in: Proceedings of the 17th International Offshore and Polar Engineering Conference, International Society of Offshore and Polar Engineers, Lisbon, Portugal, 1–6 June 2007, 652–657, 2007.
Leucci, G., Negri, S., and Carrozzo, M. T.: Ground Penetrating Radar (GPR): an application for evaluating the state of maintenance of the building coating, Ann. Geophys., 46, 481–489, 2003.
Lichey, C. and Hellmer, H. H.: Modeling giant-iceberg drift under the influence of sea ice in the Weddell Sea, Antarctica, J. Glaciol., 47, 452–460, 2001.
Løset, S.: Numerical modelling of the temperature distribution in tabular icebergs, Cold Reg. Sci. Tech., 21, 103–115, 1993a.
Løset, S.: Thermal energy conservation in icebergs and tracking by temperature, J. Geophys. Res., 98, 10001, https://doi.org/10.1029/93JC00138, 1993b.
Macheret, Y. Y., Moskalevsky, M. Y., and Vasilenko, E. V.: Velocity of radio waves in glaciers as an indicator of their hydrotherlnal state, structure and regime, J. Glaciol., 39, 373–384, 1993.
Martin, T. and Adcroft, A.: Parameterizing the fresh-water flux from land ice to ocean with interactive icebergs in a coupled climate model, Ocean Model., 34, 111–124, https://doi.org/10.1016/j.ocemod.2010.05.001, 2010.
Massom, R. A., Hill, K. L., Lytle, V. I., Worby, A. P., Paget, M. J., and Allison, I.: Effects of regional fast-ice and iceberg distributions on the behaviour of the Mertz Glacier polynya, East Antarctica, Ann. Glaciol., 33, 391–398, https://doi.org/10.3189/172756401781818518, 2001.
Merino, N., Le Sommer, J., Durand, G., Jourdain, N. C., Madec, G., Mathiot, P., and Tournadre, J.: Antarctic icebergs melt over the Southern Ocean: Climatology and impact on sea ice, Ocean Model., 104, 99–110, https://doi.org/10.1016/j.ocemod.2016.05.001, 2016.
Mingo, L. and Flowers, G.: An integrated lightweight ice-penetrating radar system, J. Glaciol., 56, 709–714, 2010.
Mingo, L., Flowers, G., Crawford, A. J., Mueller, D., and Bigelow, D. G.: A stationary impulse-radar system for autonomous deployment in cold and temperature environments, Ann. Glaciol., 81, 1–9, https://doi.org/10.1017/aog.2020.2, 2020.
Mueller, D., Crawford, A., Crocker, G., and Mingo, L.: Deterioration data collected from 'Petermann Ice Island-A-1-f' while grounded near Qikiqtarjuaq, Nunavut, 2015–2017, https://doi.org/10.21963/13091, 2019.
Natural Resources Canada: Tools and Applications, available at: http://www.nrcan.gc.ca/earth-sciences/geomatics/geodetic-reference-systems/tools-applications/10925#ppp, last access: 2016.
Oziel, L., Massicotte, P., Randelhoff, A., Ferland, J., Vladoiu, A., Lacour, L., Galindo, V., Lambert-Girard, S., Dumont, D., Cuypers, Y., Bouruet-Aubertot, P., Mundy, C.-J., Ehn, J., Bécu, G., Marec, C., Forget, M.-H., Garcia, N., Coupel, P., Raimbault, P., Houssais, M.-N., and Babin, M.: Environmental factors influencing the seasonal dynamics of spring algal blooms in and beneath sea ice in western Baffin Bay, Elem. Sci. Anth., 7, 34, https://doi.org/10.1525/elementa.372, 2019.
Sackinger, W. M., Jeffries, M. O., Li, F., and Lu, M.: Ice island creation, drift, recurrences, mechanical properties, and interactions with Arctic offshore oil production structures, Final Report for the U.S. Department of Energy, University of Fairbanks, Fairbanks, Alaska, USA, 38 pp., 1991.
Sazidy, M., Crocker, G., and Mueller, D.: A 3D numerical model of ice island calving due to buoyancy-driven flexure, in: Proceedings of the 25th International Conference on Port and Ocean Engineering under Arctic Conditions, Delft, The Netherlands, 9–13 June 2019, available at: http://www.poac.com/Papers/2019/pdf/POAC19-008.pdf (last access: March 2020), 2019.
Scambos, T., Ross, R., Bauer, R., Yermolin, Y., Skvarca, P., Long, D., Bohlander, J., and Haran, T.: Calving and ice-shelf break-up processes investigated by proxy: Antarctic tabular iceberg evolution during northward drift, J. Glaciol., 54, 579–591, 2008.
Stern, A. A., Johnson, E., Holland, D. M., Wagner, T. J. W., Wadhams, P., Bates, R., Abrahamsen, E. P., Nicholls, K. W., Crawford, A., Gagnon, J., and Tremblay, J.-E.: Wind-driven upwelling around grounded tabular icebergs, J. Geophys. Res.-Oceans, 120, 5820–5835, https://doi.org/10.1002/2015JC010805, 2015.
USGS (United States Geological Survey): Earthshots: Stellite Images of Environmental Change; Petermann Glacier, Greenland, available at: https://earthshots.usgs.gov/earthshots/node/70{#}ad-image-5-1, last access: 10 November 2019.
Wagner, T. J. W. and Eisenman, I.: How climate model biases skew the distribution of iceberg meltwater, Geophys. Res. Lett., 44, 3691–3699, https://doi.org/10.1002/2016GL071645, 2017.
Weeks, W. F. and Campbell, W. J.: Icebergs as a fresh-water source: An appraisal, J. Glaciol., 12, 207–233, 1973.
White, F. M., Spaulding, M. L., and Gominho, L.: Theoretical estimates of the various mechanisms involved in iceberg deterioration in the open ocean, Technical Report, Office of Research and Development, United States Coast Guard, Washington, DC, 133 pp., 1980.
Wilson, N.: Characterization and interpretation of polythermal structure in two subarctic glaciers, MSc thesis, University of British Columbia, Vancouver, B.C., 241 pp., 2012.
Wilson, N.: Radar Tools, Software program, https://doi.org/10.5281/zenodo.43972, 2013.
ice islands) are symbols of climate change as well as marine hazards. We measured thickness along radar transects over two visits to a 14 km2 Arctic ice island and left automated equipment to monitor surface ablation and thickness over 1 year. We assess variation in thinning rates and calibrate an ice–ocean melt model with field data. Our work contributes to understanding ice island deterioration via logistically complex fieldwork in a remote environment.
ice islands) are symbols of climate change as well as marine hazards. We...





