2.1 CMIP5 model assessment

To identify the CMIP5 models that best reproduce Southern Ocean climate, we use the root-mean-square error (RMSE) performance metric, which is common practice in model evaluation (Gleckler et al., 2008; Little and Urban, 2016; Naughten et al., 2018). We compare modelled monthly CMIP5 output of ocean potential temperature below 30^∘ S from January 1979 to December 2016 against the Hadley Centre EN4.2.1 dataset of monthly ocean potential temperature (Good et al., 2013; downloaded 8 February 2018) over the equivalent period. The observational data are corrected for biases, following the methods of Gouretski and Reseghetti (2010), and quality control flags are used to nullify potentially unreliable observations from the dataset. Models are evaluated over the whole Southern Ocean on the basis that teleconnections across the Pacific Ocean have been shown to directly influence ocean heat transport in the ASE (Steig et al., 2012). Furthermore, there are limited observations in the ASE (Mallett et al., 2018), limiting the validity of regional evaluation.

Given that the historical period defined by the CMIP5 ensemble ends in December 2005, we use ocean potential temperature projections forced with both RCP2.6 and RCP8.5 to make up the remaining decade, from January 2006 to December 2016, of the observational period. This restricts analysis to the 27 AOGCMs with projections for both RCP2.6 and RCP8.5 scenarios. Given the differences in model resolution and depth levels, we perform bilinear interpolation of the gridded model output onto the location of the observational dataset and further depth-wise linear interpolation, giving the modelled equivalent of each in situ temperature profile. We calculate two separate RMSE scores for each model, using both RCP2.6 and RCP8.5, which we average to give an overall RMSE for each CMIP5 AOGCM.

2.2 Subset selection

Based on the mean RMSE for both RCP2.6 and RCP8.5 simulations of ocean temperature in the Southern Ocean, we select the six AOGCMs with the lowest score and thus the most realistic representations of observed ocean potential temperature in the Southern Ocean. The models bcc-csm1-1, CanESM2, CCSM4, CESM1-CAM5, MRI-CGCM3 and NorESM1-ME comprise our subset. Additionally, we include the two additional models in the subset that have the highest (GISS-E2-R) and lowest (GISS-E2-H) mean projected temperature anomalies over the 21st century, local to the ASE (see below for zonal calculation), in order to capture the full range of projected temperatures on-shelf in the ASE across the CMIP5 ensemble.

2.3 Ocean temperature in the ASE

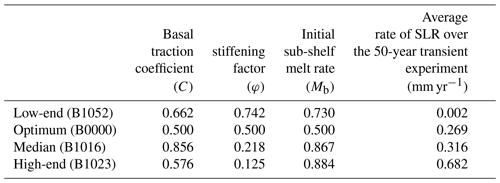
We explore modelled and observed ocean temperature in the ASE by averaging ocean temperature over the 400–700 m layer and then averaging from 103–113^∘ W and 72–74^∘ S to cover the ASE continental shelf. Depths of 400–700 m are chosen to represent the depth of CDW on-shelf (Arneborg et al., 2012; Little and Urban, 2016; Nakayama et al., 2014; Thoma et al., 2008; Webber et al., 2017). Of the models that best reproduce temperature over the Southern Ocean, the range in modelled temperature on-shelf in the ASE is ∼2 ^∘C (Fig. 1). Whilst no model is able to capture the range of observed variability in ocean temperature on-shelf, which has been shown to oscillate by up to 2 ^∘C (Jenkins et al., 2018), the collective model output captures the overall range in observed ocean temperature. Of the CMIP5 models in the subset, bcc-csm1-1, CanESM2, CCSM4 and NorESM1-ME most closely reproduce observations on-shelf in the ASE. Analysis is, however, limited by the number of observations in the region due to the seasonal dependence of ship access and lack of mooring-based observations (Kimura et al., 2017) meaning that seasonal variability is not fully captured by observations in this (or other) datasets (Mallett et al., 2018). As no single model captures the observed ocean temperature variability on-shelf, we argue that the use of a subset, as opposed to an individual model forcing, is advantageous as it covers a greater range of possible ocean temperatures on-shelf.

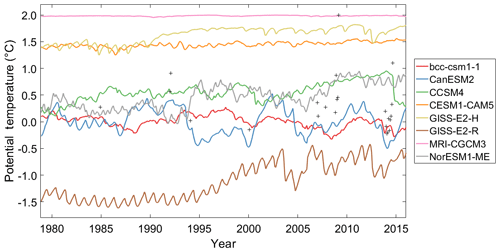
Figure 1Monthly mean ocean potential temperature in the ASE averaged over 400–700 m depth range, produced by a subset of CMIP5 AOGCMs over the period from 1979 to 2016, where the period from 2006 to 2016 is made up of projections forced with RCP8.5. Black + symbols show observed ocean potential temperature in the ASE from the Hadley Centre dataset, averaged over 400–700 m depths during the same period.

Download

2.4 CMIP5 ocean temperature projections

Having identified a subset of AOGCMs, we explore the 21st century ocean temperature projections in the ASE as modelled by each subset member. To gain uniformity of AOGCM resolution, the projection data from each CMIP5 subset member is bilinearly interpolated onto a uniform $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ horizontal grid. To prescribe a mean ocean temperature forcing for our ice sheet model experiments, we calculate the mean annual ocean potential temperature anomalies in the ASE (Fig. 2). Anomalies are calculated relative to the 2006–2016 temporally averaged mean for the ASE over the 400–700 m depth-averaged layer. The ASE is again defined as the region between 103–113^∘ W and 72–74^∘ S; a southern limit is established in order to remove regions where an ice shelf would reside as no ice shelf cavity is represented in the CMIP5 ensemble (Naughten et al., 2018). Whilst projected ocean temperatures under the RCP2.6 scenario have been obtained, the projected anomalies lie within the range of ocean temperature projections for the RCP8.5 scenario. As this investigation is interested in exploring a range of temperatures, RCP8.5 projections alone have been used in the remainder of the study.

Figure 2Projected 21st century ASE ocean potential temperature anomalies averaged over 400–700 m depth range. Anomalies are relative to the depth averaged 400–700 m mean from 2005 to 2016. Each line represents a member of the CMIP5 AOGCM subset forced with the RCP8.5 (a) and RCP2.6 (b) scenarios.

Download

The modelled range of ocean temperature anomalies under the RCP8.5 scenario diverge over the 21st century, with a 2.2 ^∘C range in anomalies by 2100. With the exception of MRI-CGCM3, all models project a temperature increase over the 21st century, relative to the 2006–2016 mean, in response to the business-as-usual scenario. Ocean warming captured by the subset is broadly consistent with the 0.66 ^∘C full CMIP5 ensemble mean warming over the 21st century in the ASE (Little and Urban, 2016). The models projecting the largest increase in temperature over the 21st century, namely GISS-E2-R, CanESM2 and bcc-csm1-1, underestimate observed temperature in the ASE during the observational period (Fig. 1). Further, the models with warm biases over the observational period, MRI-CGCM3, CESM1-CAM5 and GISS-E2-H, project the lowest temperature change over the projection period.

We attribute the projected temperature changes to modelled changes in the quantity of CDW on-shelf in the ASE (Fig. 3). The behaviour of the models can be characterized by the pattern of temperature change in the Pacific sector of the Southern Ocean, where models display either a localized warming of over 1 ^∘C in the ASE or a regional warming of a lower magnitude below 0.5 ^∘C. Models exhibiting local increases in temperature in the ASE over the projection period have broadly captured on-shelf temperature over the observational period (Fig. 1): these are, most notably, bcc-csm1-1, CanESM2, CCSM4 and NorESM1-ME. We infer the projected localized warming over the 21st century to be a result of increased incursion of the CDW layer on-shelf in the ASE. Increased CDW presence in the ASE has been observed over the last 3 decades (Schmidtko et al., 2014), a trend that is expected to continue in the 21st century as a result of a strengthening of the circumpolar westerlies that are responsible for delivering warm CDW towards the ASE continental shelf (Bracegirdle et al., 2013; Gille, 2002; Meijers et al., 2012; Sallée et al., 2013b; Spence et al., 2014).

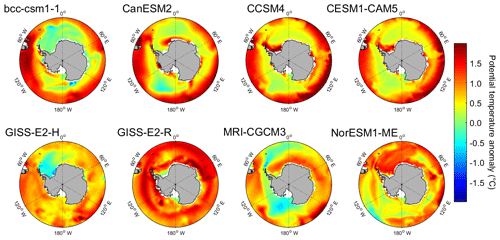
Figure 3Projected Southern Ocean temperature anomalies in 2100 (2091–2100 mean), averaged over 400–700 m depth range, under RCP8.5 relative to the 2006–2016 mean for each of the CMIP5 AOGCM subset members.

In contrast, the models that overestimate temperatures over the observational period, namely CESM1-CAM5, GISS-E2-H and MRI-CGCM3, do not display localized future warming in the ASE, instead showing a muted regional warming. We hypothesize two possible explanations for this overestimation of observed temperature: either through a modelled presence of a warm CDW layer on-shelf that does not change in depth over the course of the projection period, resulting in little to no change in mean ocean temperature, or a lack of representation of the CDW incursion mechanism that therefore precludes additional modelled upwelling or incursion.

3.1 Model description and equations

To explore the evolution of the ASE in response to CMIP5-forced sub-ice-shelf melt, we use the BISICLES ice flow model. BISICLES is based on the vertically integrated flow model by Schoof and Hindmarsh (2010), which includes longitudinal and lateral stresses, in addition to a simplification of vertical shear stress that is better applied to ice shelves and streams (Cornford et al., 2013; Schoof, 2010). It uses adaptive mesh refinement (AMR) to provide fine resolution near the grounding line and a coarser resolution elsewhere. For the simulations performed in this study, we use five resolution levels with mesh grid spacing of $\mathrm{\Delta }{x}^l={\mathrm{2}}^{-l}\times \mathrm{4000}$ m, where l is an integer between 0 and 4, giving a finest resolution of 250 m at the grounding line.

Applying mass conservation to ice thickness and horizontal velocity u gives the following equation:

where M_s denotes surface mass balance and M_b is the basal melt rate, which, when discretized, is applied solely to cells in which ice is floating.

Upper-surface elevation s is dependent on ice thickness h and bedrock elevation b, given that ice is assumed to be in hydrostatic equilibrium:

where ρ_i and ρ_w describe the respective densities of ice and water.

A two-dimensional stress balance equation is also applied, where the vertically integrated effective viscosity $\dot{\mathit{\phi }}\stackrel{\mathrm{‾}}{\mathit{\mu }}$ is obtained from both the stiffening factor φ and a vertically varying effective viscosity μ, which was derived from Glen's flow law. The stress balance equation is therefore formulated as follows:

in which the horizontal strain rate tensor is described by the following equation:

The vertically varying effective viscosity μ includes representation of vertical shear strains and, given that the flow rate exponent n=3, satisfies the following equation:

where the temperature-rate-dependent factor A(T) is calculated using the formula described by Cuffey and Paterson (2010). Uncertainty in both temperature T and A(T) is addressed by φ. The basal traction coefficient C is assumed to satisfy a non-linear power law, where $m=\mathrm{1}/\mathrm{3}$:

The initial and applied basal melt rate is parameterized so that it is spatially varying with melt concentrated closest to the grounding line according to the following equation:

where $p\left(x,y,t\right)=\mathrm{1}$ at the grounding line, which then decays exponentially with increasing distance from the grounding line:

with $\mathrm{\nabla }p\cdot n=\mathrm{0}$ as a boundary condition.

3.2 Input data

To solve the equations described above, the BISICLES ice sheet model requires numerous input data, which we find from a number of existing studies. Surface elevation (s) and surface mass balance (M_s) are obtained from Bedmap2 (Fretwell et al., 2013) and we use a 3D temperature field from a higher-order model (Pattyn, 2010). The remaining variables (C, φ, h, b and M_b) are obtained from the results of an initialization procedure of BISICLES performed by Nias et al. (2016). Of these parameters, the basal traction coefficient (C) and viscosity stiffening factor (φ) are found by solving an optimization problem, which minimizes the mismatch between modelled ice surface speed and the observed speed from Rignot et al. (2011). Here we use the ice thickness (h) and a modified bed topography (b) developed by Nias et al. (2016), which was found by modifying BedMap2 using an iterative procedure to smooth inconsistencies in the modelled flux divergence. The initial sub-shelf melt rate (M_b) is also calculated through this iterative procedure (Nias et al., 2016) to ensure the melt rate at the beginning of the simulation is consistent with present day observations and matches observed thinning at the grounding line. Further, the model has been run with a calving front fixed at its initial position.

3.3 CMIP5 melt rate forcing

We convert the CMIP5 projections of ocean temperature into a mean additional ocean sub-shelf melt forcing using the linear relationship between temperature anomaly and ice shelf melting, which is approximated for the ASE (Rignot and Jacobs, 2002), where an additional 0.1 ^∘C temperature increase results in an increase of 1 m a⁻¹ to the basal melt rate. The CMIP5 AOGCM forcing data that we use are relatively coarse in their spatial resolution and also do not capture sub-ice-shelf oceanographic conditions. Consequently, we are unable to accurately incorporate the spatial complexity of ocean temperature variability that exists in the ASE (Turner et al., 2017). Given that our input data better reflect regional rather than local-scale oceanic changes, we force our simulations with spatially averaged CMIP5 temperature anomalies.

The additional sub-shelf melt forcing is applied to the model using a distance decay function with the greatest melt rates located at the grounding line to capture some of the spatial distribution of melt (Payne, 2007). We use a grounding line proximity parameter p as a multiplier, where p=1 at the grounding line and decays exponentially with increasing distance. In the 1D case, $p\left(x\right)=\exp (-x/\mathit{\lambda })$, where λ is a scale of 10 000 m. The mean additional forcing is applied onto a 2D spatially varying field, smoothed to match the pattern of melt obtained during the model initialization procedure.

The simplified distance-dependent melt parameterization employed in this investigation was chosen in order to maintain continuity with the Nias et al., (2016, 2019) studies. Our parameterization neglects the effect of overturning circulation within an ice shelf cavity in addition to the ice shelf cavity geometry and presence of meltwater plumes that influence the pattern of sub-ice-shelf basal melting (Dinniman et al., 2016). Whilst more complex parameterizations attempt to incorporate these mechanisms (e.g. Lazeroms et al., 2018; Reese et al., 2018), no parameterization is yet able to replicate known patterns of sub-ice-shelf melting (Favier et al., 2019). Furthermore, the uncertainty associated with the magnitude of the future forcing exceeds that associated with the parameterization of sub-shelf melting (Holland et al., 2019), justifying the use of the simplified parameterization employed in this investigation.

3.4 Parameter selection

We investigate the impact of parameter uncertainty on the response of the ASE to the CMIP5 ocean forcing by selecting members of a perturbed parameter ensemble performed by Nias et al. (2016), which hereafter we will refer to as the N16 ensemble. Here we will briefly describe the N16 ensemble, before explaining our selection process. As described above, the initialization procedure performed by Nias et al. (2016) produces three optimal, spatially varying fields of the unknown parameters of basal traction coefficient C, ice stiffening factor φ and initial basal melting M_b over the ASE catchment. The N16 ensemble explores the influence of uncertainty in these parameters on the modelled mass evolution and grounding line migration in the ASE by scaling the optimal parameter fields between a halving and a doubling and proceeding to sample these scaled fields using a Latin hypercube. The resulting unique combinations of scaled parameters are referred to in this investigation as parameter sets. For each perturbed parameter set, a 50-year BISICLES simulation was performed and the change in volume above floatation (VAF) was used to calculate a sea level equivalent (SLE) contribution. This was done for each combination of two geometries (modified and unmodified Bedmap2) and two sliding laws, giving a total of 284 simulations.

In order to explore the role of parameter uncertainty in our study, we select three sets of perturbed parameter fields from the N16 ensemble, in addition to the optimum. To represent a crude 90 % confidence from the variation in parameters, we select the parameter combinations that generated a high-end, median and low-end SLE contribution over a 50-year transient experiment in the absence of additional forcing. We identify the parameter sets that most closely produce the 5th and 95th percentile of a calibrated probability density function of the N16 ensemble, as described in Nias et al. (2019). In this investigation we solely consider the simulations with the non-linear sliding law and modified bedrock. For each parameter set, we perform simulations forced with the CMIP5 ocean temperature projections parameterized as a sub-ice-shelf melt rate. We present the scaling factors for the four parameter sets used in this investigation (Table 1). The scaling factors describe the level of perturbation for each of the spatially varying parameter fields within each of the four parameter sets where a halving is 0, the optimum is 0.5 and a doubling is 1. When discussing the outcome of the results, we will use these values as a relative comparison.

Table 1Scaling factors applied to each of the spatially varying parameter fields for the parameter sets selected from the N16 ensemble.

Download Print Version | Download XLSX

3.5 Experimental design

We perform regional simulations of the ASE sector on the domain defined in Cornford et al. (2015). For each of the four different parameter sets, we use parameterized sub-ice-shelf melt rates for each of the eight CMIP5 subset members. An additional control experiment is performed for each of the four parameter sets. The control experiment has no additional melt forcing, and therefore the results capture the dynamical ice response to present conditions. A total of 36 experiments are performed. The following results section firstly describes the results from the optimum parameter set, followed by the results of the experiments using the three perturbed parameter sets.

For our simulations of future mass evolution of the ASE in response to changing ocean temperature forcing, we choose to keep the atmospheric forcing constant due to the small effect of surface mass balance changes on ice stream dynamics (Seroussi et al., 2014), particularly on the timescales we explore in this investigation. Furthermore, ocean-forced sub-shelf melting elicits an immediate response to the upstream ice dynamics (Seroussi et al., 2014) making this the focus of our work.

4.1 Optimum parameter set

Our projections show that by the end of the 21st century the CMIP5-forced sub-ice-shelf melting in the ASE will lead to a contribution to global mean sea level of 2.0–4.5 cm under the RCP8.5 scenario. The range in SLE in response to each CMIP5 sub-ice-shelf melt rate reflects the magnitude of the applied forcing (Fig. 4), where the experiments forced with CMIP5 models that project the most extreme temperature change result in the greatest overall mass contribution over the 21st century. The variation in response according to AOGCM forcing indicates a strong dependence of ASE mass loss on sub-shelf melting, consistent with existing literature (Gudmundsson et al., 2019; Pritchard et al., 2012). The most extreme response is a result of the GISS-E2-R projected ocean melting in the ASE, which results in 4.5 cm of sea level rise. The model that projects the lowest-magnitude ocean temperature forcing, MRI-CGCM3, projects a contribution of 2.0 cm by 2100, despite having a negligible temperature change at the end of the 21st century relative to present day. In contrast, the contribution from the control experiment indicates a committed 2.2 cm contribution to sea level rise in response to recent past and present day forcing. The SLE contribution over the projection period is non-linear for models with more extreme forcing, which reflects the projected non-linear increase in ocean potential temperature (Fig. 2).

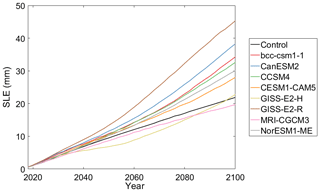
Figure 4Projected 21st century SLE from the ASE in response to ocean temperature forcing projected by a subset of CMIP5 AOGCMS under the RCP8.5 scenario.

Download

Each of the nine experiments project grounding positions in 2100 retreat relative to the initial grounding line positions (Fig. 5). The response of the individual ice streams to the varying ocean melt forcings differs as a result of their varying topographic confinements and differing ice dynamics (Nias et al., 2016). Despite the differing magnitudes of the CMIP5 model forcings, the PIG grounding line migrates 25 km upstream from its initial position for all experiments except MRI-CGCM3 and the control experiment wherein retreat is 11 km, likely controlled by the steep deepening of the bed over the initial 10 km upstream of the initial grounding line (Vaughan et al., 2006). Stabilization of the grounding line 25 km upstream of its initial location is indicative of local topographic maxima at this position (Vaughan et al., 2006) and substantial prograde slope evident in the modified Bedmap2 topography described in the N16 study. We infer from the results that, using the optimum parameter set, grounding line migration over the 21st century is relatively insensitive to the magnitude of additional forcing, as illustrated by the equivalent grounding line positions. The results from the control experiment denote the projected grounding line migration should climate conditions remain constant and therefore reveal the committed sea level contribution from the ASE in response to current climate.

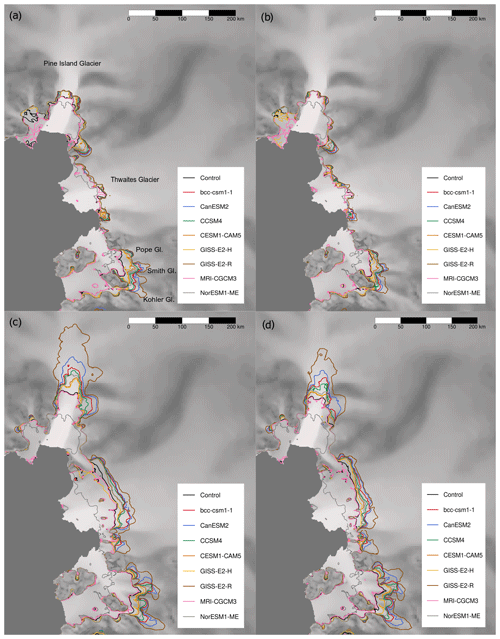
Figure 5ASE ice stream grounding line position in 2100 in response to each CMIP5-AOGCM-projected ocean temperature forcing under RCP8.5 for each parameter set: (a) optimum, (b) low end, (c) median, (d) high end. The grey grounding line is the initial position.

Across the model subset, the Thwaites Glacier grounding line is projected to both retreat and lengthen over the 21st century, with a greater retreat occurring in the eastern side of the main trunk. A lengthening of the grounding line occurs due to the widening of the ice stream trunk upstream of the grounding line. In response to the varying forcings, the Thwaites Glacier grounding line experiences approximately the same extent of grounding line migration, which is clustered at points across the main trunk, showing a level of insensitivity to applied forcing. The exception to this grounding line position is illustrated by the GISS-E2-R-forced experiment, where migration of the Thwaites Glacier grounding line is marginally greater than for the remaining models. The relative insensitivity of Thwaites Glacier is consistent with previous modelling studies (Tinto and Bell, 2011), which may suggest that the buttressing effect of the unconfined ice shelf is minimal and varying magnitudes of sub-shelf melting have a lesser control on the grounding line position (Parizek et al., 2013). Furthermore, retreat to the same position upstream would indicate that this is a position of stability, where the grounding line is pinned, likely reflecting the presence of a topographic rise. The fact that migration and lengthening of the grounding line occurs even in the control experiment demonstrates that grounding line retreat over the 21st century is almost certain.

Grounding line retreat of the Pope, Smith and Kohler (PSK) ice streams is dependent on the magnitude of the CMIP5 sub-ice-shelf melt forcing applied. The most extreme forcing, the GISS-E2-R-forced experiment, results in almost complete loss of grounded area of the small ice streams by the end of the 21st century, whilst the control experiment results in grounding line retreat of only ∼20 km. The variation in grounding line positions in 2100 indicates that the PSK ice streams are sensitive to the magnitude of ocean forcing, due to the buttressing provided by the narrow embayment of the ice streams and the confined Crosson and Dotson ice shelves (Konrad et al., 2017). As the ice streams are relatively small compared to their neighbours, almost complete loss of the present ice streams could occur over the 21st century, even in the absence of additional ocean forcing (Scheuchl et al., 2016).

4.2 Perturbed parameter sets

The range in volume above floatation change from the subset of experiments results in a −0.02–1.4 cm SLE contribution for the low-end parameter set, 2.6–8.6 cm for the median parameter set and 5.4–12.1 cm for the high-end parameter set. As illustrated by the differing range of SLE contributions across the four parameter sets, the sensitivity of the ASE to different additional sub-shelf melt forcings varies with differing spatially varying parameter fields. Again, the magnitude of mass loss is proportional to the magnitude of the applied forcing for each of the CMIP5-forced experiments, and this relationship is consistent across the three perturbed parameter sets.

Experiments configured with the low-end parameter set result in the most modest grounding line retreat across the ASE ice streams (Fig. 5). The PIG grounding line is projected to retreat ∼14 km upstream of the main trunk for each of the CMIP5-forced experiments, with retreat into the southwestern tributary occurring in some scenarios in response to the different forcing magnitudes. The projected grounding line position of Thwaites Glacier by the end of the 21st century for the low-end parameter set is most equivalent to the present day position, experiencing minimal retreat with only minor variation between the different CMIP5-forced experiments. Of the ASE ice streams, the Thwaites Glacier grounding line position varies most in comparison to the optimum. Similar to the optimum parameter set experiments, the PSK grounding line retreat differs considerably in response to the varying CMIP5 forcings, with the greatest retreat occurring in response to the GISS-E2-R forcing. Overall, the grounding line positions under the low-end parameter configuration are similar to the optimum. Mass loss and grounding line retreat is limited under this configuration due to the increased stiffness and greater basal traction, limiting delivery of ice to the grounding line and subsequent mass loss.

In comparison to the low-end and optimum parameter sets, the median and high-end parameter sets produce considerable grounding line retreat in response to each of the CMIP5-projected sub-ice-shelf melt forcings. Both parameter sets have a similarly low scaling of the ice viscosity and a high initial basal melt rate in comparison to the optimum, which is likely responsible for the greater mass loss (Nias et al., 2016). The median set of parameters results in a greater grounding line retreat over the 21st century than the high-end parameter set, despite the lower overall mass loss. This occurs because the high-end parameter set has a lower scaling factor applied to the basal traction coefficient field than the median set, producing a more slippery bed in the former than the latter, causing increased delivery of mass toward the grounding line and offsetting grounding line retreat. Combined with softer ice and increased velocity, the relatively slippery bed also results in increased delivery of mass across the grounding line, explaining the high projected mass loss and SLE contribution of between 5.4 and 12.1 cm by 2100, despite the more muted grounding line retreat.

The response of the individual ice streams to additional melt forcing is similar for the median and high-end parameter sets. The PIG grounding line retreat is predominantly confined to its narrow embayment with considerable upstream retreat into the main trunk. For both parameter sets, the PIG grounding line is sensitive to the magnitude of the CMIP5 ocean temperature forcing, with large differences between the final positions in 2100 across the subset. The Thwaites Glacier grounding line experiences a considerable lengthening across the wide glacier trunk for each of the CMIP5-forced experiments, in addition to an upstream retreat where the widening of the embayment has a greater control on the mass flux from the ice stream. For all parameter sets, the PSK ice streams exhibit notable grounding line retreat, controlled largely by the varying magnitudes of applied ocean forcing.

There is a significant correlation between the rate of SLE contribution and the applied CMIP5 ocean anomaly, with an R² value of >0.9, which is consistent for each of the parameter sets (Fig. 6b). Whilst the response of the ASE ice streams to ocean temperature forcing is linear for each parameter set, the sensitivity to forcing is dependent on the parameter set chosen in the ice sheet model configuration, modifying both the gradient and intercept of the SLE response to temperature forcing. Moreover, the uncertainty associated with the projected SLE contribution for each AOGCM is dependent on the parameter set (Fig. 6b), where models with the greatest ocean temperature forcing result in the largest range in SLE contribution when accounting for the parameter uncertainty.

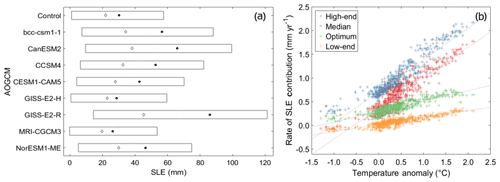
Figure 6(a) Sea level equivalent contribution from the ASE in 2100 for each AOGCM in the subset under the RCP8.5 scenario for the range of parameter sets. The top and tail of the boxes show the high- and low-end perturbed parameter sets, respectively. The diamond and circle show the SLE contribution for the optimum and median parameter sets, respectively. (b) Rate of SLE response against ocean temperature anomaly in the ASE, averaged over the 400–700 m layer, over the projection period from 2017 to 2100 for each set of parameters.

Download