the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Revisiting Austfonna, Svalbard, with potential field methods – a new characterization of the bed topography and its physical properties
Marie-Andrée Dumais
Marco Brönner
With hundreds of metres of ice, the bedrock underlying Austfonna, the largest icecap on Svalbard, is hard to characterize in terms of topography and physical properties. Ground-penetrating radar (GPR) measurements supply ice thickness estimation, but the data quality is temperature dependent, leading to uncertainties. To remedy this, we include airborne gravity measurements. With a significant density contrast between ice and bedrock, subglacial bed topography is effectively derived from gravity modelling. While the ice thickness model relies primarily on the gravity data, integrating airborne magnetic data provides an extra insight into the basement distribution. This contributes to refining the range of density expected under the ice and improving the subice model. For this study, a prominent magmatic north–south-oriented intrusion and the presence of carbonates are assessed. The results reveal the complexity of the subsurface lithology, characterized by different basement affinities. With the geophysical parameters of the bedrock determined, a new bed topography is extracted and adjusted for the potential field interpretation, i.e. magnetic- and gravity-data analysis and modelling. When the results are compared to bed elevation maps previously produced by radio-echo sounding (RES) and GPR data, the discrepancies are pronounced where the RES and GPR data are scarce. Hence, areas with limited coverage are addressed with the potential field interpretation, increasing the accuracy of the overall bed topography. In addition, the methodology improves understanding of the geology; assigns physical properties to the basements; and reveals the presence of softer bed, carbonates and magmatic intrusions under Austfonna, which influence the basal-sliding rates and surges.
During the last few decades, with satellite technology advancement and an increased need to understand climate change, the polar regions have become an important laboratory for studying ongoing environmental changes. In this context, icecaps, icefields and glaciers are of interest, as they are highly sensitive to climate variations (Vaughan et al., 2013; Dowdeswell et al., 1997). Glacial sliding and melting rates are often determined from Global Positioning System (GPS) measurements, satellite imagery and satellite altimetry (e.g. Przylibski et al., 2018; Bahr et al., 2015; Grinsted, 2013; Radić et al., 2013; Dunse et al., 2012; Gray et al., 2015; Moholdt et al., 2010b). The ice thickness and the ground topography at the glacier base, key factors in understanding the glacial-sliding and ice-melting mechanisms (Clarke, 2005), have proven challenging to derive. The glacier deformation mechanisms and sliding depend on the glacier roughness, the rheological properties of the bed, the distribution of the rheological properties of the ice and the hydrological system at the ice–bed interface (e.g. Gong et al., 2018; Gladstone et al., 2014; Olaizola et al., 2012; Clarke, 2005). Presence of sediments may also contribute to bed deformation, resulting in ploughing (basal sliding; e.g. Eyles et al., 2015; Iverson et al., 2007; Bamber et al., 2006; Boulton and Hindmarsh, 1987; Clarke, 1987). Thus, determining the glacier bed lithology is as critical as determining its topography to assess glacier responses to climate variations.
Ground-penetrating radar (GPR) is the preferred method to retrieve the glacial bed topography; however, scattering from englacial meltwater streams and dielectric absorption often hamper accurate imaging of the bed, especially for temperate ice. For temperatures at pressure melting point, common in temperate glaciers, liquid water is present at the ice–bed interface. The correctness of the resulting topography depends on several glacier parameters, including density, porosity and the water content fraction, which determine the permittivity and, therefore, the radio wave velocity used to derive the thickness (Lapazaran et al., 2016). These parameters cannot be directly measured and are highly influenced by temporal and spatial variations of the water content fraction distribution through the glacier (Barrett et al., 2007; Navarro et al., 2009; Jania et al., 2005).
Using GPR and radio-echo sounding (RES) measurements from several campaigns, a bed topography has been derived for Austfonna on Svalbard (Fürst et al., 2018; Dunse et al., 2011). In this paper, we test the feasibility of retrieving the glacier thickness of Austfonna with airborne gravity data, as they are sensitive to the density contrast between the ice and the bedrock. Adding magnetic interpretation to the study contributes by indicating variations in the bedrock lithology and the density distribution, which must be considered to accurately derive ice thickness and bedrock topography. Combined gravity–magnetic interpretation is a powerful tool to define basement types and identify the presence of various geological structures, such as sedimentary basins under the ice in the bedrock. Gravity and magnetic methods have been used in the past for basement lithology studies in the Arctic (e.g. Gernigon et al., 2018; Døssing et al., 2016; Nasuti et al., 2015; Gernigon and Brönner, 2012; Olesen et al., 2010; Barrère et al., 2009) and for sea ice and glacier studies (e.g. An et al., 2017; Gourlet et al., 2015; Tinto et al., 2015; Zhao et al., 2015; Porter et al., 2014; Tinto and Bell, 2011; Studinger et al., 2008, 2006; Spector, 1966). In this study, we combine these methods with GPR data to obtain both an accurate glacial bed topography and also an understanding of the rheological changes of the basement. Magnetic and gravity modelling were used to assess the feasibility of retrieving topographical and geophysical properties in terms of ice thickness, bed softness, the presence of carbonates and till, and bed topography.
With a geographic area of 8357 km2, Austfonna, seen in Fig. 1, is the largest icecap on the Svalbard archipelago (Dallmann, 2015). It is located on Nordaustlandet, the second-largest island in Svalbard, northeast of Spitsbergen, and approximately 80 % of it is covered by ice. Austfonna has one main central dome with an ice thickness of up to 600 m (Dowdeswell et al., 1986) and feeds several drainage basins. Considered polythermal, consisting of a mixture of temperate and cold ice, it is relatively flat at its highest elevation and includes both land-terminating and tidewater glaciers. Studies suggest its basal temperature is near the pressure melting point (Dunse et al., 2011); thus Austfonna experiences basal sliding and subglacial water might be present. Surging, or surge-type, glaciers have also been observed in the area (Schytt, 1969). Other studies link surging to the softness of the bedrock and tectonically active zones (e.g. Jiskoot et al., 2000). The bedrock topography (including cavities and obstacles), geothermal sources and the presence of sediments are also contributing factors to the glacier basal-sliding velocities (e.g. Boulton and Hindmarsh, 1987; Clarke, 1987).
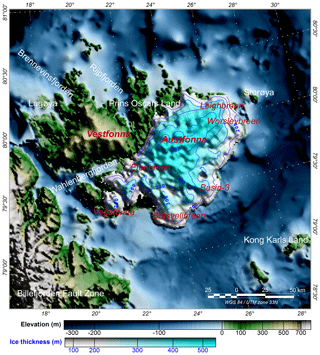
Figure 1Surface topography map of Nordaustlandet, east of Spitsbergen, Svalbard, and the Austfonna icecap from Dunse et al. (2011). Approximately 80 % of Nordaustlandet is covered by ice, and the ice thickness is up to ca. 600 m. Polythermal and relatively flat at its highest elevation, Austfonna hosts both land-terminating and tidewater glaciers of which several have been observed to surge.
During the last few decades, several campaigns have aimed to retrieve the underlying bedrock topography of Austfonna using RES (Moholdt et al., 2010a; Dowdeswell et al., 1986) and GPR (Dowdeswell et al., 2008; Dunse et al., 2011). Acquired profiles are shown in Fig. 2. McMillan et al. (2014) and Moholdt et al. (2010a, b) applied satellite altimeter data to estimate surface elevation changes and ice loss. They observed a significant increase in the dynamic activity and the outlet flow rate of the glaciers Vestfonna (Schäfer et al., 2012) and Austfonna (McMillan et al., 2014). Over 28 % of the area covered by Austfonna rests below sea level (Dowdeswell et al., 1986). Moreover, the lowest elevations of the bedrock are located at the tips of Basin 3 in the southeast and Leighbreen in the northeast, (Fig. 1), with bed elevation values of 150 and 130 m below sea level, respectively (Dunse et al., 2011; Dowdeswell et al., 2008).
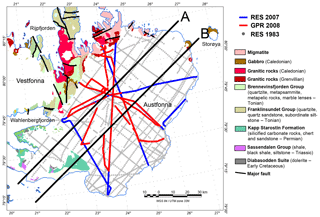
Figure 2Geological map of Austfonna with GPR and RES campaign lines and gravity–magnetic profiles A and B (modified from Dallmann, 2015, and Dunse et al., 2011). The interpreted profiles, labelled A and B, have been chosen to cover a large area of Austfonna and to capture important geological trends.
The geology underneath the ice is barely understood, as very few outcrops are available to identify the main geological structures and basement affinity of Nordaustlandet (Fig. 2). However, based on the studied outcrops, the geology appears to be complex and the exposed rocks are dated to various geological epochs (Dallmann, 2015; Johansson et al., 2002). Basement outcrops at Wahlenbergfjorden identify different types of basements on each side of the fjord (Dallmann, 2015), which is assumed to represent a major geological north–south (N–S) division of the island. For the northern shore of the fjord and north of Nordaustlandet (including the totality of Vestfonna), the regional map of Lauritzen and Ohta (1984) and radiometric dating (Ohta, 1992) indicate a pre-Caledonian basement with Mesoproterozoic and Neoproterozoic rock exposures, mainly composed of metasedimentary rocks like marble, quartzite and mica schist. The rocks are significantly folded and faulted due to the Caledonian-deformation influence but not to the same degree as in the rest of Svalbard. Caledonian and Grenvillian Rijpfjorden granites are found on the northern tip of Nordaustlandet on Prins Oscars Land (Johansson et al., 2005, 2002). In the east, the bedrock comprises mainly Silurian diorites and gabbros as seen on Storøya (Johansson et al., 2005). On the southern shore of Wahlenbergfjorden, an abundance of Carboniferous to Permian limestones and dolomites with Early Cretaceous doleritic intrusions are exposed. Dallmann (2015) consequently concluded that the same geological demarcation observed at Wahlenbergfjorden continues under Austfonna. The southern basement of Austfonna is believed to be much younger than the one in the north and is composed of unmetamorphosed post-Caledonian rocks. The youngest rocks in Nordaustlandet are Jurassic–Cretaceous doleritic dikes, which intrude into the Tonian basement rocks (composed of dolomite, sandstone, quartzite and limestone) on the island of Lågøya, and the Meso- to Neoproterozoic basement composed of basal conglomerate, volcanic breccias and migmatites in the outlet of Brennevinsfjorden, northwest of Vestfonna (Overrein et al., 2015). South of Nordaustlandet, dolerite sills were emplaced during the Cretaceous in Kong Karls Land. Evidence of the locations of the sills can be found in seismic-reflection and magnetic data in the vicinity of Nordaustlandet (Polteau et al., 2016; Minakov et al., 2012; Grogan et al., 2000).
The magnetic map is a compilation of two datasets compiled from campaign flights flown in 1989 and 1991 (Table 1). The data are sparse with line spacing of 4 to 8 km at a target ground clearance of 900 m. Having been originally processed by different entities with different processing algorithms, the datasets are reprocessed to a similar level. A control line, flown during both campaigns as an overlap, is used to level the two datasets to each other. This step ensures that the two datasets are levelled to the standard International Geomagnetic Reference Field (IGRF) model (Thébault et al., 2015) and the compilation is smooth at the overlap.
The magnetic map (Fig. 3b) presents strong parallel anomalies crossing the centre of Nordaustlandet, oriented N–S. The magnetic intensity is correlated with the type and level of magnetization, which in turn is mainly related to the iron content, time of formation or metamorphic processes of the minerals found in the basement. Thus, the magnetization is a strong indicator of the mineralogy of the basement and its lithology. The strong anomaly observed across Austfonna also intersects the Caledonian Rijpfjorden granites, which have been identified on the geology map (Johansson et al., 2005). This anomaly is also parallel to the Billefjorden fault zone and to the Caledonian frontal thrust (Gernigon and Brönner, 2012; Barrère et al., 2009). The Caledonian is also associated with magmatic episodes. Northeast of Nordaustlandet, the sharp and low-frequency magnetic anomalies created by the known emplaced Cretaceous sills have a distinct and prominent signature.
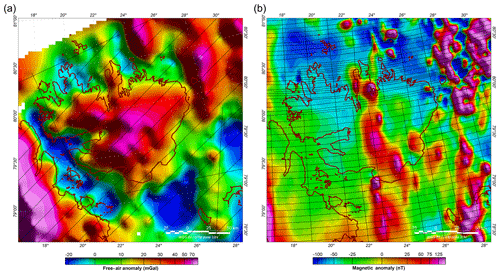
Figure 3(a) Free-air gravity map and (b) a magnetic anomaly map of Nordaustlandet with the acquisition flight lines denoted by the thin black lines. The gravity data are sensitive to an excess or loss of mass. Low free-air gravity data are often linked to sedimentary basins. The magnetic data show important N–S-trending anomalies crossing Nordaustlandet and intersecting with the Caledonian Rijpfjorden granites.
The gravity data were acquired during a 1998–1999 campaign (Forsberg and Olesen, 2010; Forsberg et al., 2002). The flight routes were along a southwest–northeast (SW–NE) direction with a spacing of 18 km and at a ground clearance of 1 km (Table 1). The free-air anomaly map is presented in Fig. 3a. The gravity data produced 4000 m cell size grids with a standard deviation of ∼2 mGal over a 6000 m half-wavelength resolution. Gravity lows are seen in the south and southwest of Nordaustlandet, with a higher signal on the icecap reflecting the ice coverage and its thickness. Gravity is sensitive to the density contrast between the various geological bodies and ice in this case. Low-gravity measurements reflect low densities, which are often linked to sediment accumulation or sedimentary basins.
The grid resolution provides an estimate of the smoothness level of the data and of the limitations to the modelling and data filtering. Given the magnetic grid resolution, features shallower than 2 km cannot be accurately resolved. Depth interpretations and body geometry are limited by the grid resolution. A single anomaly normally leads to several geometry and depth possibilities. In this paper, the most favourable possibility is chosen for its consistency with the GPR and RES investigations and for model simplicity. Therefore, depth estimates from the models in the present paper represent the deepest depth possibility and are limited by a 2 km resolution. The magnetic data also present several asymmetric anomalies which can be interpreted by dipping bodies. However, given the coarseness of the data, a simple model without dipping is preferred.
Dunse et al. (2011) have presented a bedrock topography compilation with a 1 km spatial grid resolution from data acquired by RES and GPR, but the geospatial distribution of the measurements (Fig. 2) suggests lower resolution in areas with poor coverage. With these data, combined with the ice surface topography published by the Norwegian Polar Institute (NPI) in 1998 (Norwegian Polar Institute, 1998), an ice thickness is derived for Austfonna. This step allows for an estimate of the volume and mass of the icecap to derive the gravitational effect of the glacier. The density contrast and the topography of the bedrock–ice interface contribute to the sharpest and most prominent gravity effects. A valid approach to resolve the bedrock topography is to assume a simple basement geometry with a homogeneous density. Analogous to sedimentary-basin interpretation (Bott, 1960) and treating the glacier as an infinite slab, the free-air anomaly (FAc) along a profile is reconstructed as follows:
where G is the gravitational constant (), ρ the density, hbed the topography of the bed above sea level, and hice and Hice the thickness of ice above sea level and below sea level, respectively. The full extent of the ice thickness is represented by (hice+Hice). The free-air anomaly is referenced to the geoid. In the reconstruction of the free-air anomaly, the ice above sea level is regarded as an excess of mass, whereas the ice below sea level is considered a mass deficiency. The influence of the ice () depends on the surrounding media, which include air (, negligible) and the bed () in this case. This reduction technique is valid under the condition that the thickness of the ice is smaller than the horizontal dimensions of the icecap by several magnitudes. As GPR and RES data were acquired solely onshore, only onshore gravity acquisition was considered in the model for comparison.
Assuming the difference between the free-air anomaly observed (FAo) and the free-air anomaly calculated is caused by erroneous bed topography measurements, the correction of the bed topography is as follows:
On average, this correction is 2 m for the analysis along the gravity profiles above Austfonna. With a standard deviation of 63 m, the difference in thickness varies between −190 and 290 m. The difference in thickness is applied to the initial bedrock topography derived from GPR and RES. Given the wide line spacing of the gravity profiles, both datasets are gridded with the same resolution (4000 m) for the analysis (Fig. 4). The highest summits of the bed topography remain at the same level. Small residual discrepancies are largely due to the approximation of an infinite slab and the accuracy of the various datasets. It should be noted that both GPR–RES depth measurements and gravity ice thickness were calculated with the same ice surface topography dataset which acts as a control variable. It reduces the influence of the resolution and accuracy of the ice surface topography when comparing the two bed topography models. However, important discrepancies exist, for example, under Vegafonna on the southwest corner of Austfonna and under Leighbreen and Worsleybreen, northeast of Austfonna. These areas are discussed in detail in later sections when magnetic data are included in the interpretation. Less prominent misfits occur at the outer edge of the marine-terminating glaciers Basin 3 and Bråsvellbreen, where the ice surface topography and glacier geometry might undergo rapid and drastic variations, and where relatively faster ice surface velocities were observed in comparison to the thick, flat interior icecap (Gladstone et al., 2014; Moholdt et al., 2010a). As the ice surface topography and gravity data were acquired around the same time but independently of each other, the resolution and accuracy of the ice surface topography increase the misfit where the glacier geometry is most susceptible to drastic variations. Notably, the gravity profiles cross the glacier perpendicular to its flow and parallel to the shore with an uneven mass distribution; i.e. more mass is found on the northern side of the profile. This terrain effect is commonly corrected for in gravity processing for extreme topography relief (Lafehr, 1991) but requires accurate terrain topography acquired through methods such as laser scanning data acquisition or a high-resolution digital elevation model.
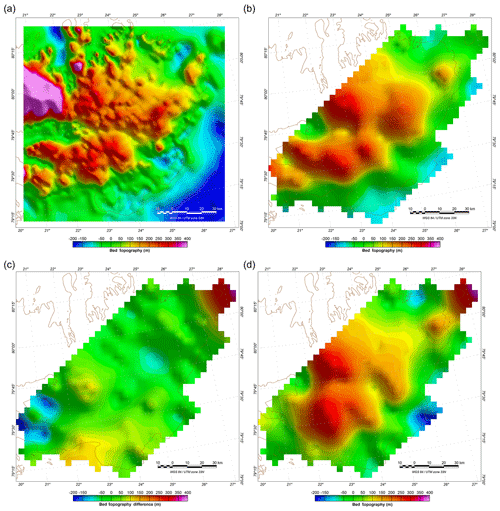
Figure 4Bed topography derived from RES and GPR (a), bed topography derived from RES and GPR gridded along gravity acquisition flight lines (b), corrections applied to the bed topography (c) and bed topography corrected for gravity measurements gridded along gravity profiles (d). Major discrepancies with deviations greater than 150 m occur under Vegafonna (southwest) and Leighbreen and Worsleybreen (northeast).
Interpretation using 2-D forward modelling determines the interface between contrasting bodies of different magnetizations and densities. It provides depth and geometrical insights into lithological variations in the bedrock. The forward modelling (Fig. 5) is carried out along the actual airborne gravity lines to ensure the highest resolution of the gravity data. Two lines are modelled and referred to as profiles A and B (Fig. 2). The modelled profiles were chosen for their location and coverage. They contain several aspects of the geology under Austfonna (such as basements and intrusions), and they are located near or above RES and GPR measurements. Models are initially constrained by the bedrock topography derived by Dunse et al. (2011) and are independent of the free-air bed topography corrections. The measured data points from the GPR and RES are highlighted (purple circles, Fig. 5a).
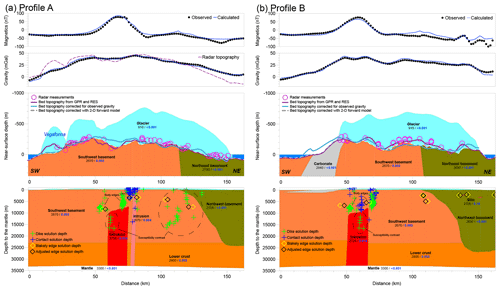
Figure 5Observed and calculated magnetic and gravity profiles (top), the near-surface view of the basements (middle) and the depth to the mantle (bottom) for profile A (a) and profile B (b), as defined in Fig. 2, with Werner deconvolution indicators of the intrusions and the basement interfaces. A gravity response (purple solid lines) is calculated for a homogeneous bedrock using GPR–RES bed topography. The misfit with the observed gravity measurements suggests the bedrock is heterogeneous and the bed topography from the radar needs refining. The gravity-corrected bed topography (blue lines in the near-surface view panel) is an improvement but fails to recognize the heterogeneity of the bed. The 2-D forward model (dashed white line) improves the accuracy of the bed topography by using a density more representative of the lithology. Each section representing a geological body is characterized with a density (kg m−3; black values) and a susceptibility (SI units; blue values). Dike solution depths (green crosses), contact solution depths (blue crosses), Blakely edge solution depths (yellow diamonds) and adjusted-edge solution depths (black diamonds) are identified.
Initial petrophysical parameters are assigned based on the comprehensive petrophysical database from mainland Norway (Olesen et al., 2010) provided by the Geological Survey of Norway (NGU) and on the described bedrock types (Dallmann, 2015). The basement is forward modelled according to gravity and magnetic signatures, using the software package GM-SYS (Geosoft, 2006). The mantle–crust boundary, i.e. the Mohorovičić discontinuity (Moho), was set at a depth of around 33 km following the interpretation of Ritzmann et al. (2007). In the northeast of Austfonna, the basement seems to have a very low magnetization (less than 0.001 SI), but a density higher than the surrounding media (2700 kg m−3) is required to fit the observed field.
Along profile A (Fig. 5a), reducing the density in the southwest of Austfonna (where Vegafonna is located) was attempted but could not be fit to the observed free-air anomaly. Introducing layers of till with a density of 1600 kg m−3 did not significantly reduce the signal to account for the observed gravity data unless the till had a thickness of several hundreds of metres. Thus, the GPR–RES bed topography is adjusted in this area to be consistent with the gravity measurements. This discrepancy is more important under a region with scarce GPR and RES measurements (measurements are indicated with purple circles). A similar interpretation was made along profile B, where misfits between the two methods occur and only a few measurements exist. The GPR–RES data were not acquired in a grid pattern, and therefore the GPR–RES bed topography proposed in these discrepancy areas is the result of a gridding interpolation between profiles and data points. The bed topographies calculated from the free-air analysis and interpreted from magnetic and gravity modelling agree in general and suggest corrections to the GPR–RES topography in the same direction. However, misfits exist, since the free-air analysis presented in the previous section considers a homogenous basement, while the model interpretation indicates variable densities. The difference between the GPR–RES bed topography and the 2-D forward-model bed topography varies from −170 to 80 m with a standard deviation of 40 m. A smaller level of correction is required with the 2-D forward model than predicted from the gravity correction. The 2-D forward model accounts both for a certain degree of confidence in the GPR–RES data and for the bedrock density variation.
The centres of both profiles are characterized by a high magnetic anomaly requiring high susceptibility. This anomaly is a prominent and continuous N–S-oriented anomaly, which might at least be partly linked to exposed granites on Prins Oscars Land at the northern tip of Nordaustlandet. A relatively high density of 2725–2750 kg m−3 is assigned to this granitic intrusion. However, granites with comparable densities and susceptibilities are found on the mainland of Norway in Vest-Agder, Rogaland and Telemark (NGU petrophysics database available at http://geo.ngu.no/GeosciencePortal/, last access: 29 March 2019; 2016). Werner deconvolution (Phillips, 1997; Ku and Sharp, 1983; Werner, 1955), an automated depth-to-source estimation method, was applied to help quantify the depth and morphology of magnetic bodies under Austfonna (Fig. 5a and b). Using these empirical basement indicators that are sensitive to susceptibility variations, and approximating the geological source to a simplified geometry of features such as contacts and dikes (Goussev and Peirce, 2010), the depth and edges of intrusions were estimated. Euler deconvolution (Thompson, 1982; Reid et al., 1990), with a structural index of 1 (for dike and sill models), was also used to compare the results. This method uses horizontal and vertical derivatives along with a predetermined structural index to estimate the source location. In our case, Euler deconvolution analyses provide similar depth values to those from Werner deconvolution analyses. Both Werner and Euler deconvolution analyses determined the existence of a dike at a depth of about 8 km with a width of almost 20 km. While Euler deconvolution results in a dike seated at 8 km, Werner deconvolution resolves the top of this intrusion to be tilted with a depth from 8 km in the southwest to 6 km in the northeast. A second dike was determined at a 2 km depth (or 1.5 km with Euler deconvolution) with a much narrower width of 2 km and was only seen on profile A, indicating a dike also shorter in length. The model suggests shallow magnetized bodies exist off the shore of Nordaustlandet with a depth of less than 2 km. These indications are used in the model to constrain the depth of the intrusions. Given the accuracy of the data, a certain degree of freedom is allocated to those indicators to fit the observed data with the geology expected.
The gridded tilt derivative of an anomaly, at a location x, y (Miller and Singh, 1994), characterizes the angle of the ratio between the amplitudes of the vertical derivative and the horizontal derivative. Thus, the zero contour indicates the border of a geological body where a density or susceptibility contrast with the surrounding media occurs. This indication from the magnetic tilt derivative (Fig. 6) was used to constrain the lateral extent of the intrusions. Blakely et al. (2016) have also developed a method to retrieve the edge of a body and its depth (Fig. 5) by using the reciprocal of the horizontal gradient at the zero contour of the tilt derivative grid (Fairhead et al., 2008; Salem et al., 2007). At high magnetic latitudes for a vertical dike geometry, the depth is estimated as equal to the half-width of the magnetic anomaly (Hinze et al., 2013). The lateral edge of the body is adjusted accordingly to the depth found with Blakely's method (2016). This reduces the size of the magnetic body (Fig. 5) to the minimum size required for this depth. Thus, a first magnetic body with a susceptibility 0.004 SI in a 0.003 SI surrounding, a density of 2670 kg m−3, a width of 3 km and a depth of 2 km is modelled. The top of the second intrusion is deeper (10 km) and wider (15 km) with higher magnetic and density properties (0.016 SI and 2750 kg m−3). For both profiles, the difference between the bed topography from the magnetic–gravity interpretation and the gravity estimation is caused by the large density intrusion located in the basement.
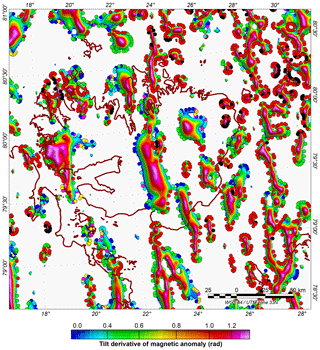
Figure 6The tilt derivative of the magnetic anomaly superimposed by Blakely depth estimation is used to determine the location and depth of geological bodies and to constrain the model. Negative data are nulled. Sill bodies located in northeast Austfonna, both onshore and offshore, are generally shallower than the large and deep N–S-trending granitic intrusions crossing Austfonna.
Along profile B, anomalies of smaller sizes are found on the eastern coastline of Austfonna. The nature of the magnetic signal and the results from Euler and Werner deconvolutions suggest the existence of shallow magmatic bodies such as sills. For simplification, they were modelled with a common magnetization value for sills of 0.15 SI susceptibility (Hunt et al., 1995). Another major difference between the two profiles modelled is the higher-density body (2840 kg m−3) located west of the intrusions on profile B. The NPI geological map identifies a carbonate outcrop in this area of Austfonna. This carbonate body has a strong influence on the gravity signal, which is critical in the estimation of the bed topography (turquoise topography, Fig. 5b). Locally, the bed has a much higher density and should be considered when making bed topography corrections. The magnetic and gravity modelling provides an indication of this carbonate depth, orientation and thickness. Given the coarseness of the data and their limitations, the carbonate body is expected to be shallower and thinner.
The results from the 2-D modelling of profiles A and B are summarized in Fig. 7. According to the models, a prominent deep-seated, highly magnetic intrusion occurs underneath Austfonna crossing N–S, and the bedrock is divided into two types of basement with different geophysical properties.
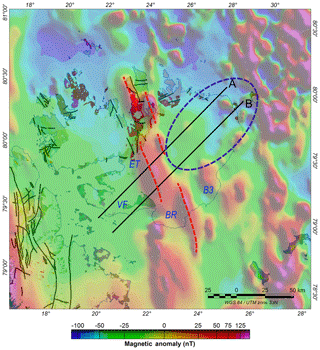
Figure 7Profiles A and B, as defined in Fig. 2, against the magnetic anomaly and NPI geological map. Dashed red lines represent deep intrusion trends across Austfonna and the blue circle represents the change of basement seen on the lines modelled (B3: Basin 3; ET: Etonbreen; BR: Bråsvellbreen; VF: Vegafonna).
Given the densities and susceptibilities used and the presence of granites on the northern part of the island, the intrusion is likely to be granitic. It is probably of a different composition than the exposed rocks, since the modelled granitic densities indicate relatively high values but are within the expected values for granites (2500–2810 kg m−3; Telford et al., 1990). Moreover, given the N–S-trending faults system across Svalbard, a similar process could explain the strong magnetic anomalies trending N–S and crossing Nordaustlandet. Major faults on Svalbard, trending N–S to north-northwest–south-southeast (NNW–SSE), have been reactivated and juxtaposed by strike-slip motion over several geological periods before, during and after the Caledonian orogeny (Dallmann, 2015). Granites were emplaced during the late stages of the Caledonian (late Silurian to Early Devonian) (Dallmann, 2015). One could argue the presence of N–S-striking sills in the near-offshore region could correspond to the magnetic signature seen under Austfonna. However, the frequency content of the magnetic signal (derived from high-frequency filters or vertical derivatives), the size of the structures revealed from tilt derivative signals and the depth estimates from Werner deconvolution suggest the existence of a rather wide (15 km), deep-seated (10 km) dike intrusion or dike complex onshore and shallow bodies offshore and on the coastline of Austfonna. In addition to the granite affinities suggested by the susceptibility and density interpreted in the 2-D forward models, the high magnetic anomalies correspond to the geological mapping of the observed granites (Fig. 7). Therefore, granite intrusions are proposed to exist in Nordaustlandet bedrock, such as the Caledonian Rijpfjorden granites seen on the central northern tip of Nordaustlandet (Johansson et al., 2005). These intrusions, trending N–S to NNW–SSE like the major faults found on Prins Oscars Land, suggest the faults are present and continue under Austfonna.
Along profile B, sill intrusions are modelled on the eastern coastline, where shallow sills have been previously interpreted and related to a tholeiitic phase (130–100 Ma) linked to the spreading of the Amerasia Basin in the Arctic Ocean and the uplift initiated by the mantle plume on the Yermak Plateau, northwest of Svalbard (Polteau et al., 2016; Minakov et al., 2012; Grogan et al., 2000).
Densities found under southwest Austfonna are also lower compared to the northeastern region. This is consistent with the terrain observations under the Etonbreen and Bråsvellbreen basins (Dunse et al., 2015, 2011), suggesting a more erodible bedrock in the southwestern area. It correlates with the late Paleozoic platform composed of limestones, dolomites, carbonate rocks and sedimentary rocks to the southwest of Austfonna compared to the metasedimentary rocks (marble, quartzite and mica schist) from the pre-Caledonian basement found to the northeast. Furthermore, the 2-D model suggests a smoother bed topography than the one suggested by GPR–RES measurements, which is consistent with a more erodible basement. While two types of bedrock are already expected from outcrop samples, the analysis of the two profiles suggests an oblique division (NE–SW) between the two basement types rather than a N–S division. The younger basement is more constrained to the northeast of Austfonna than previously thought. An oblique division of the basement is consistent with the major fault system found on Svalbard and the geological provinces division (often separated by faults), both trending N–S to NNW–SSE (Harland et al., 1974; Flood et al., 1969).
Additional magnetic and gravity data improve the bed accuracy and the spatial resolution by filling gaps in the GPR–RES data. Austfonna bed topography was assessed and recalculated using free-air anomaly measurements. The bed topography was enhanced and refined using the 2-D model interpretation, and its physical properties were extracted. Given the scarce sampling of the GPR–RES data under Vegafonna, the discrepancies might be due to gridding interpolation (Fig. 3), as previously discussed. Similarly, along profile B, the poorer fit of the bed topography derived from GPR and RES with the magnetic and gravity model is caused by the scarcer availability of GPR–RES data. Another source of error is the accumulation of water in the erodible basement, causing an increase in uncertainty and underestimation of the ice thickness. The magnetic and gravity data provide consistent and regular coverage over the full area and are less sensitive to gridding interpolation. Gravity data processing requires the use of high-precision GPS measurements, which were estimated to have a 0.5 m vertical accuracy (Forsberg et al., 2002). In comparison, the distribution of GPR and RES measurements shows irregularities mainly due to the poor navigational guidance available at the time of acquisition (Dowdeswell et al., 1986; GlaThiDa Consortium, 2019). The navigational errors caused flight-line distortions and wider line spacings in certain areas. Positional errors were estimated as ±250 m (Dowdeswell et al., 1986). Therefore, the GPR–RES bed topography is more prone to gridding interpolation artefacts. GPR–RES measurements are susceptible to thickness errors in the presence of steep bed slopes, where the signal is reflected from a lateral wall instead of the bottom topography. While often corrected with a 2-D migration processing technique that corrects for the direction of profiling, transversal slopes are not corrected unless 3-D migration is used (Lapazaran et al., 2016; Moran et al., 2000). The water content in the glacier and the bedrock increases internal scattering and the dielectric absorption. It also affects the radio wave velocity, which contributes to the error in the time-to-thickness conversion (Brown et al., 2017; Lapazaran et al., 2016; Blindow et al., 2012; Matsuoka, 2011). Temporal and spatial variations of radio wave velocity account for uncertainties in ice thickness reconstruction (Jania et al., 2005; Navarro et al., 2014). The magnetic and gravity interpretation compensates indirectly for these errors, as it is less sensitive to water content in the bedrock and offers an additional control on the properties of the bedrock. The magnetic data show the bedrock heterogeneity, associated with susceptibility variations within the glacier bed, indicating different bedrock types and lithologies. These lithological changes suggest the presence of geological boundaries and provide constraints to assigning density changes. Thus, the magnetic data improve the final bed topography accuracy, as they provide constraints on the density distribution for the bed underlying the glacier. The effect of geology on gravity inversion for glacial bed topography was also noticed in other studies (An et al., 2019, 2017; Hodgson et al., 2019).
Using Austfonna bed topography and lithology derived from the 2-D forward model, the theoretical gravity response was modelled for ice loss by removing iteratively uniform and homogeneous layers of ice (Fig. 8). The model predicts that an ice thickness variation of 10 m causes an average variation in gravity of ∼0.5 mGal, which is resolved by state-of-the-art gravity measurements. Thus, the gravity anomaly is mainly driven by the bedrock topography and its physical properties, providing hard evidence of the interface between the ice and the rock. The cell size of the GPR–RES-gridded bed topography is 1000 m with extensive interpolation between the measurements. Flown in 1998–1999, the gravity data produced 4000 m cell size grids with a standard deviation of ∼2 mGal over a 6000 m half-wavelength resolution. Bed topography corrections with gravity data are more effective than GPR–RES gridding interpolation algorithms. The spatial resolution of airborne gravity measurements depends on the gravimeter together with the platform stability, line spacing, acquisition speed and distance to the source. A state-of-the-art fixed-wing airborne gravimeter, flown with the appropriate flight parameters, can produce 200 m cell size grids with a precision of ∼0.5 mGal over a 3000–4000 m half-wavelength resolution (e.g. An et al., 2019, 2017; Studinger et al., 2008). Therefore, using gravity modelling increases the confidence in and the accuracy of the bedrock topography under a glaciated area. Improvement of the spatial resolution of the final bed topography could also be achieved with the appropriate survey parameters and a denser line spacing for the gravity data.
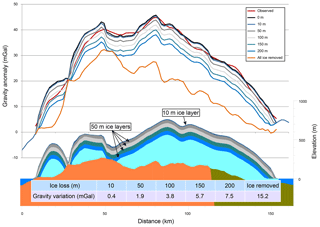
Figure 8Predicted gravity signature variations with ice loss. The gravity response is calculated using, as the initial state, the 2-D forward model from profile A with the currently known ice thickness. Uniform layers of ice with thicknesses of 10, 50, 100, 150 and 200 m are removed from the model. The first 10 m layer of ice loss yields a gravity anomaly of approximately 0.5 mGal. Significant ice loss is detectable from long-term observations.
Till, commonly found at the base of the glacier, can account for the misfit between the observed and modelled gravity but could not be resolved given the resolution of the dataset. For a variation of 1 mGal, 50 m of till (1600 kg m−3) needs to be emplaced in the model. Lower flight elevation and denser line spacing acquisition is required to model the till. For the accurate interpretation of till modelling, additional independent measurements are required, such as magnetic data which are sensitive to the susceptibility contrast with the surrounding bedrock.
Due to their chemical composition, calcium carbonate rocks erode subglacially and migrate in the glacier system along various transportation paths (Bukowska-Jania, 2007). Calcite dissolution and precipitation have an impact on the calcite saturation of the water film that lubricates the bed–glacier interface, and they modify the bed morphology and roughness through melting and regelation processes (Ng and Hallet, 2002). The model from profile B suggests carbonate rocks underlie the glacier, and it maps the lateral extent of the body by an additional 7–8 km under the ice. While the thickness of the carbonate is small compared to the resolution of the data, the gravity measurements suggest an important excess of mass at that location but with no susceptibility variation from the surrounding media. Therefore, we must expect there to be a prominent volume of carbonate with an assumed density of 2840 kg m−3.
Deep intrusions, possibly granites, and shallow sills were located and delineated from the 2-D forward model. Characterization of these intrusions provides information about the potential variation of the bed lithology in terms of thermal conductivity. Geothermal heat flux, resulting from the decay of radioactive isotopes present in the glacier bed, may raise the temperature of the basal ice and affect the ice sliding (Paterson and Clarke, 1978). Granites are prone to higher geothermal heat flux due to their mineral composition. On Austfonna, only one borehole has been drilled to reach the bedrock and provide heat flux information in the summit area, indicating a geothermal heat flux of ∼40 mW m−2 (Ignatieva and Macheret, 1991; Zagorodnov et al., 1989). There are no other direct observations available to estimate this heat flux. However, our study suggests that this measurement may not be representative for the entire bed underlying Austfonna.
Located outside the 2-D modelled profiles, a high-intensity anomaly is apparent under Basin 3, subject to a high negative ice surface elevation change rate (Gladstone et al., 2014; Moholdt et al., 2010a). Due to the large variation of the ice surface topography in recent years (and decades), retrieving a valid ice topography for the gravity model has proven difficult. However, the results from profiles A and B with the Euler deconvolution, Werner deconvolution and Blakely depth methods indicate a basement that resembles the softer southwestern basement, largely intruded with shallow (less than 2 km) sills and deeper (8 km) granitic intrusions. Such physical properties are possible drivers for the high basal-sliding rate and surge mechanisms and can be linked to the high ice surface elevation changes seen on Basin 3. Further studies of the granitic intrusion and thermal modelling would be of great interest to link the geothermal flux under Basin 3 to ice changes currently observed.
The interpretation of the two profiles provides an insight into the basement and intrusion geology and a refined glacial bed topography, specifically where GPR and RES data are scarce and less reliable. These findings enhance the understanding of the regional geology of the area and demonstrate the potential to reconstruct the full bed lithology with the aid of high-resolution gravity and magnetic data. Granitic intrusions are known to be potential geothermal sources and can locally affect the heat flux profile of Austfonna. These intrusions can be linked to the basal sliding of Austfonna, and analyzing them can lead to a better understanding of the sliding mechanisms in the area.
Airborne magnetic and gravity data were used to study the Austfonna icefield basement on Svalbard. Considering a homogenous basement, the GPR–RES bed topography was corrected with gravity measurements. We demonstrated the importance of the geology for a gravity inversion to calculate the bed topography and presented a method that integrates magnetic, gravity, GPR and RES data. Several interpretation techniques (Euler deconvolution, Werner deconvolution, 2-D modelling) were used to create a model of the bedrock with assigned physical properties in terms of size, depth, susceptibility and density. These results suggest the bed topography derived from GPR–RES measurements can be corrected with gravity analysis, while knowledge of the basement lithology and/or magnetic interpretation further increases its reliability. Thus, the bed topography model derived from magnetic and gravity measurements contributes to a more accurate estimation of ice volume. One of the main challenges is that the data were acquired in different campaigns, in different years and with different acquisition patterns. On the other hand, this approach expands the coverage of the model. Given the difficulty of accessing the underlying lithology of Austfonna, increasing the magnetic and gravity coverage is an effective method to assess the physical properties of the basement.
Moreover, the geophysical interpretation provides insight into the geological and structural affinity of the basement under Austfonna. While the presence of two basement types on Nordaustlandet is well accepted, the new interpretation allows the boundary between the basements to be mapped. The physical properties of the basements provide indications of the basement types for softness and erodibility and provide information about the type of intrusions likely found under the icefield. Sills, granitic intrusions and carbonate rocks have been interpreted in the model and their evolution was set in a geotectonic time frame. Each of these geological bodies has a different impact on the basal thermal regime and the erodibility of the basement, consequently leading to heterogenous basal-ice-sliding rates.
The temperature of the ice at the base, which controls the basal thermal regime, is usually determined by ice thickness, ice advection, ice surface temperature, geothermal heat and frictional heat (related to softness and topography). Irregular basal topography leads to complex localized patterns of the thermal regime. The lithology identified with potentially higher radiogenic heat production can be correlated with areas of faster ice surface velocities or ice thickness variations. Here, with additional petrophysical properties from collected rock samples, thermal modelling is necessary and will help to improve understanding of the different geothermal domains and their effects on Austfonna basal thermal regimes. In this paper, the resolution of the datasets limits the resolution of the geometry of the geological features modelled. Higher-resolution data from state-of-the-art instrumentation, i.e. gravimeters, GPS units, GPR, RES devices and magnetometers, would further refine the physical properties of the basement and allow for a full reconstruction of the bed lithology and topography.
Bed elevation data are available from Dunse et al. (2011). Magnetic and revised bed topography data are available on the Geological Survey of Norway Geoscience Portal (http://geo.ngu.no/GeosciencePortal/search, last access: 21 November 2019; Geological Survey of Norway Geoscience Portal, 2016; contact person is Marie-Andrée Dumais). Gravity data are available upon request from the Norwegian Mapping Authority (contact person is Ove Omang) or on the Geological Survey of Norway Geoscience Portal.
MAD reprocessed the airborne magnetic dataset and produced the bed topography from the gravity data and the 2-D forward model. MB assisted in the data interpretation and commented on the paper.
The authors declare that they have no conflict of interest.
We would like to thank Thorben Dunse for providing the GPR–RES bed and related surface elevation maps and for his helpful discussions on the data. We thank Rene Forsberg and Ove Omang for providing the airborne gravity data. Chantel Nixon is also acknowledged for English proofreading of an earlier version of the paper. We thank Daniel Farinotti and the three anonymous reviewers for their valuable comments that improved the manuscript.
This paper was edited by Daniel Farinotti and reviewed by three anonymous referees.
An, L., Rignot, E., Elieff, S., Morlighem, M., Millan, R., Mouginot, J., Holland, D. M., Holland, D., and Paden, J.: Bed elevation of Jakobshavn Isbrae, West Greenland, from high-resolution airborne gravity and other data, Geophys. Res. Lett., 44, 3728–3736, https://doi.org/10.1002/2017gl073245, 2017.
An, L., Rignot, E., Millan, R., Tinto, K., and Willis, J.: Bathymetry of Northwest Greenland Using “Ocean Melting Greenland” (OMG) High-Resolution Airborne Gravity and Other Data, Remote Sens., 11, 131, https://doi.org/10.3390/rs11020131, 2019.
Bahr, D. B., Pfeffer, W. T., and Kaser, G.: A review of volume-area scaling of glaciers, Rev. Geophys., 53, 95–140, https://doi.org/10.1002/2014RG000470, 2015.
Bamber, J. L., Ferraccioli, F., Joughin, I., Shepherd, T., Rippin, D. M., Siegert, M. J., and Vaughan, D. G.: East Antarctic ice stream tributary underlain by major sedimentary basin, Geology, 34, 33, https://doi.org/10.1130/g22160.1, 2006.
Barrère, C., Ebbing, J., and Gernigon, L.: Offshore prolongation of Caledonian structures and basement characterisation in the western Barents Sea from geophysical modelling, Tectonophysics, 470, 71–88, https://doi.org/10.1016/j.tecto.2008.07.012, 2009.
Barrett, B. E., Murray, T., and Clark, R.: Errors in radar CMP velocity estimates due to survey geometry, and their implication for ice water content estimation, J. Environ. Eng. Geophys., 12, 101–111, https://doi.org/10.2113/jeeg12.1.101 2007.
Blakely, R. J., Connard, G. G., and Curto, J. B.: Tilt Derivative Made Easy, Geosoft Technical Publications, 4, 1–4, 2016.
Blindow, N., Salat, C., and Casassa, G.: Airborne GPR sounding of deep temperate glaciers – Examples from the Northern Patagonian Icefield, 2012 14th International Conference on Ground Penetrating Radar (GPR), 664–669, 2012.
Bott, M. H. P.: The use of rapid digital computing methods for direct gravity interpretation of sedimentary basins, Geophys. J. Royal Astro. Soc., 3, 63–67, https://doi.org/10.1111/j.1365-246x.1960.tb00065.x, 1960.
Boulton, G. S. and Hindmarsh, R. C. A.: Sediment deformation beneath glaciers: rheology and geological consequences, J. Geophys. Res., 92, 9059-9082, https://doi.org/10.1029/JB092iB09p09059, 1987.
Brown, J., Harper, J., and Humphrey, N.: Liquid water content in ice estimated through a full-depth ground radar profile and borehole measurements in western Greenland, The Cryosphere, 11, 669–679, https://doi.org/10.5194/tc-11-669-2017, 2017.
Bukowska-Jania, E.: The role of glacier system in migration of calcium carbonate on Svalbard, Pol. Polar Res., 28, 137–155, 2007.
Clarke, G. K. C.: Subglacial till: A physical framework for its properties and processes, J. Geophys. Res., 92, 9023–9036, https://doi.org/10.1029/jb092ib09p09023 1987.
Clarke, G. K. C.: Subglacial Processes, Ann. Rev. Earth Planet. Sci., 33, 247–276, https://doi.org/10.1146/annurev.earth.33.092203.122621, 2005.
Dallmann, W. K.: Geoscience Atlas of Svalbard, Norsk polarinstitutt Rapportserie, 2015.
Døssing, A., Jaspen, P., Watts, A. B., Nielsen, T., Jokat, W., Thybo, H., and Dahl-Jensen, T.: Miocene uplift of the NE Greenland margin linked to plate tectonics: Seismic evidence from the Greenland Fracture Zone, NE Atlantic, Tectonics, 35, 1–26, https://doi.org/10.1002/2015tc004079, 2016.
Dowdeswell, J., Drewry, D., Cooper, A., Gorman, M., Liestøl, O., and Prheim, O.: Digital mapping of the Nordaustlandet ice caps from airborne geophysical investigations, Ann. Glaciol., 8, 51–58, https://doi.org/10.1017/s0260305500001130, 1986.
Dowdeswell, J. A., Hagen, J. O., Björnsson, H., Glazovsky, A. F., Harrison, W. D., Holmlund, P., Jania, J., Koerner, R. M., Lefauconnier, B., Ommanney, C. S. L., and Thomas, R. H.: The Mass Balance of Circum-Arctic Glaciers and Recent Climate Change, Quaternary Res., 48, 1–14, https://doi.org/10.1006/qres.1997.1900, 1997.
Dowdeswell, J. A., Benham, T. J., Strozzi, T., and Hagen, J. O.: Iceberg calving flux and mass balance of the Austfonna ice cap on Nordaustlandet, Svalbard, J. Geophys. Res., 113, F03022, https://doi.org/10.1029/2007JF000905, 2008.
Dunse, T., Greve, R., Schuler, T. V., and Hagen, J. O.: Permanent fast flow versus cyclic surge behavior: numerical simulations of the Austfonna ice cap, Svalbard, J. Glaciol., 57, 247–259, https://doi.org/10.3189/002214311796405979, 2011.
Dunse, T., Schuler, T. V., Hagen, J. O., and Reijmer, C. H.: Seasonal speed-up of two outlet glaciers of Austfonna, Svalbard, inferred from continuous GPS measurements, The Cryosphere, 6, 453–466, https://doi.org/10.5194/tc-6-453-2012, 2012.
Dunse, T., Schellenberger, T., Hagen, J. O., Kääb, A., Schuler, T. V., and Reijmer, C. H.: Glacier-surge mechanisms promoted by a hydro-thermodynamic feedback to summer melt, The Cryosphere, 9, 197–215, https://doi.org/10.5194/tc-9-197-2015, 2015.
Eyles, N., Boyce, J. I., and Putkinen, N.: Neoglacial (<3000 years) till and flutes at Saskatchewan Glacier, Canadian Rocky Mountains, formed by subglacial deformation of a soft bed, Sedimentology, 62, 182–203, https://doi.org/10.1111/sed.12145, 2015.
Fairhead, J. D., Salem, A., Williams, S., and Samson, E.: Magnetic interpretation made easy: The Tilt-Depth-Dip- ΔK method, SEG Technical Program Expanded Abstracts 2008, 779–783, https://doi.org/10.1190/1.3063761, 2008.
Flood, B., Gee, D. G., Hjelle, A., Siggerud, T., and Winsnes, T. S.: The Geology of Nordaustlandet, northern and central parts, Norsk Polarinstitutt Skrifter, 146, 1969.
Forsberg, R. and Olesen, A. V.: Airborne Gravity Field Determination, in: Sciences of Geodesy – I: Advances and Future Directions, edited by: Xu, G., Springer Berlin Heidelberg, Berlin, Heidelberg, 83–104, 2010.
Forsberg, R., Olesen, A. V., Keller, K., and Møller, M.: Airborne gravity survey of sea areas around Greenland and Svalbard 1999–2001, Survey and processing report – KMS Technical Report, 18, 2002.
Fürst, J. J., Navarro, F., Gillet-Chaulet, F., Huss, M., Moholdt, G., Fettweis, X., Lang, C., Seehaus, T., Ai, S., Benham, T. J., Benn, D. I., Björnsson, H., Dowdeswell, J. A., Grabiec, M., Kohler, J., Lavrentiev, I., Lindbäck, K., Melvold, K., Pettersson, R., Rippin, D., Saintenoy, A., Sánchez-Gámez, Schuler, T. V., Sevestre, H., Vasilenko, E., and Braun, M. H.: The Ice-Free Topography of Svalbard, Geophys. Res. Lett., 45, 11760–711769, https://doi.org/10.1029/2018GL079734, 2018.
Geological Survey of Norway Geoscience Portal, available at: http://geo.ngu.no/GeosciencePortal/search (last access: November 2019), 2016.
Geosoft: GM-SYS profile modeling. Gravity and Magnetic Modeling Software, v. 4.10, Geosoft Incorporated, p. 116, 2006.
Gernigon, L. and Brönner, M.: Late Palaeozoic architecture and evolution of the southwestern Barents Sea: insights from a new generation of aeromagnetic data, Journal of the Geological Society, London, 169, 449–459, https://doi.org/10.1144/0016-76492011-131, 2012.
Gernigon, L., Brönner, M., Dumais, M.-A., Gradmann, S., Grønlie, A., Nasuti, A., and Roberts, D.: Basement inheritance and salt structures in the SE Barents Sea: Insights from new potential field data, J. Geodynam., 119, 82–106, https://doi.org/10.1016/j.jog.2018.03.008, 2018.
Gladstone, R., Schäfer, M., Zwinger, T., Gong, Y., Strozzi, T., Mottram, R., Boberg, F., and Moore, J. C.: Importance of basal processes in simulations of a surging Svalbard outlet glacier, The Cryosphere, 8, 1393–1405, https://doi.org/10.5194/tc-8-1393-2014, 2014.
GlaThiDa Consortium: Glacier Thickness Database 3.0.1, World Glacier Monitoring Service, Zurich, Switzerland, https://doi.org/10.5904/wgms-glathida-2019-03, 2019.
Gong, Y., Zwinger, T., Åström, J., Altena, B., Schellenberger, T., Gladstone, R., and Moore, J. C.: Simulating the roles of crevasse routing of surface water and basal friction on the surge evolution of Basin 3, Austfonna ice cap, The Cryosphere, 12, 1563–1577, https://doi.org/10.5194/tc-12-1563-2018, 2018.
Gourlet, P., Rignot, E., Rivera, A., and Casassa, G.: Ice thickness of the northern half of the Patagonia Icefields of South America from high-resolution airborne gravity surveys, Geophys. Res. Lett., 43, 241–249, https://doi.org/10.1002/2015GL066728, 2015.
Goussev, S. A. and Peirce, J. W.: Magnetic basement: gravity-guided magnetic source depth analysis and interpretation, Geophys. Prosp., 58, 321–334, https://doi.org/10.1111/j.1365-2478.2009.00817.x, 2010.
Gray, L., Burgess, D., Copland, L., Demuth, M. N., Dunse, T., Langley, K., and Schuler, T. V.: CryoSat-2 delivers monthly and inter-annual surface elevation change for Arctic ice caps, The Cryosphere, 9, 1895–1913, https://doi.org/10.5194/tc-9-1895-2015, 2015.
Grinsted, A.: An estimate of global glacier volume, The Cryosphere, 7, 141–151, https://doi.org/10.5194/tc-7-141-2013, 2013.
Grogan, P., Nyberg, K., Fotland, B., Myklebust, R., Dahlgren, S., and Riis, F.: Cretaceous Magmatism South and East of Svalbard: Evidence from Seismic Reflection and Magnetic Data, Polarforschung, 68, 25–34, 2000.
Harland, W. B., Cutbill, J. L., Friend, P. F., Gobbett, D. J., Holliday, D. W., Maton, P. I., Parker, J. R., and Wallis, R. H.: The Billefjorden fault zone, Spitsbergen: the long history of a major tectonic lineament, Norsk Polarinstitutt Skrifter, 161, 1974.
Hinze, W., Von Frese, R., and Saad, A.: Gravity and magnetic exploration: Principles, practices and applications, Cambridge University Press, 2013.
Hodgson, D. A., Jordan, T. A., De Rydt, J., Fretwell, P. T., Seddon, S. A., Becker, D., Hogan, K. A., Smith, A. M., and Vaughan, D. G.: Past and future dynamics of the Brunt Ice Shelf from seabed bathymetry and ice shelf geometry, The Cryosphere, 13, 545–556, https://doi.org/10.5194/tc-13-545-2019, 2019.
Hunt, C. P., Moskowitz, B. M., and Banerjee, S. K.: Rock physics and phase relations, A Handbook of Physical Constants: AGU Reference Shelf, Americain Geophysical Union Vol. 3, 189–204, 1995.
Ignatieva, I. Y. and Macheret, Y. Y.: Evolution of Nordaustlandet ice caps in Svalbard under climate warming, Glaciers-Ocean-Aonosphere Interactions, Proceedings of the International Symposium held at St Petersburg, September 1990, IAHS Publ. no. 208, 208, 301–312, 1991.
Iverson, N. R., Hooyer, T. S., Fischer, U. H., Cohen, D., Moore, P. L., Jackson, M., Lappegard, G., and Kohler, J.: Soft-bed experiments beneath Engabreen, Norway:regelation infiltration, basal slip and bed deformation, J. Glaciol., 53, 323–340, https://doi.org/10.3189/002214307783258431, 2007.
Jania, J., Macheret, Y. Y., Navarro, F. J., Glazovsky, A. F., Valisenko, E. V., Lapazaran, J. J., Glowacki, P., Migala, K., Balut, A., and Piwowar, B. A.: Temporal changes in the radiophysical properties of a polythermal glacier in Spitsbergen, Ann. Glaciol., 42, 125–134, https://doi.org/10.3189/172756405781812754, 2005.
Jiskoot, H., Murray, T., and Boyle, P.: Controls on the distribution of surge-type glaciers in Svalbard, J. Glaciol., 46, 412–422, https://doi.org/10.3189/172756500781833115, 2000.
Johansson, Å., Larionov, A. N., Tebenkov, A. M., Ohta, Y., and Gee, D. G.: Caledonian granites of western and central Nordaustlandet, northeast Svalbard, GFF, 124, 135–148, https://doi.org/10.1080/11035890201243135, 2002.
Johansson, Å., Gee, D. G., Larionov, A. N., Ohta, Y., and Tebenkov, A. M.: Grenvillian and Caledonian evolution of eastern Svalbard – a tale of two orogenies, Terra Nova, 17, 317–325, https://doi.org/10.1111/j.1365-3121.2005.00616.x, 2005.
Ku, C. C. and Sharp, J. A.: Werner deconvolution for automated magnetic interpretation and its refinement using Marquart's inverse modeling, Geophysics, 48, 754–774, https://doi.org/10.1190/1.1441505 1983.
Lafehr, T. R.: Standardization in gravity reduction, Geophysics, 56, 1170–1178, 1991.
Lapazaran, J. J., Otero, J., Martín-Español, A., and Navarro, F. J.: On the errors involved in ice-thickness estimates I: groundpenetrating radar measurement errors, J. Glaciol., 62, 1008–1020, https://doi.org/10.1017/jog.2016.93, 2016.
Lauritzen, Ø. and Ohta, Y.: Geological map of Svalbard 1:500,000. Sheet 4G, Nordaustlandet, Nor. Polarinst. Skr. 154C, 1984.
Matsuoka, K.: Pitfalls in radar diagnosis of ice-sheet bed conditions: Lessons from englacial attenuation models, Geophys. Res. Lett., 38, L05505, https://doi.org/10.1029/2010gl046205, 2011.
McMillan, M., Shepherd, A., Gourmelen, N., Dehecq, A., Leeson, A., Ridout, A., Flament, T., Hogg, A., Gilbert, L., Benham, T. J., van den Broeke, M., Dowdeswell, J. A., Fettweis, X., Noël, B., and Strozzi, T.: Rapid dynamic activation of a marine-based Arctic ice cap, Geophys. Res. Lett., 41, 8902–8909, https://doi.org/10.1002/2014gl062255, 2014.
Miller, H. G. and Singh, V.: Potential field tilt - a new concept for the location of potential field sources, J. Appl. Geophys., 32, 213–217, https://doi.org/10.1016/0926-9851(94)90022-1, 1994.
Minakov, A., Mjelde, R., Faleide, J. I., Flueh, E. R., Dannowski, A., and Keers, H.: Mafic intrusions east of Svalbard imaged by active-source seismic tomography, Tectonophysics, 518–521, 106–118, https://doi.org/10.1016/j.tecto.2011.11.015, 2012.
Moholdt, G., Hagen, J. O., Eiken, T., and Schuler, T. V.: Geometric changes and mass balance of the Austfonna ice cap, Svalbard, The Cryosphere, 4, 21–34, https://doi.org/10.5194/tc-4-21-2010, 2010a.
Moholdt, G., Nuth, C., Hagen, J. O., and Kohler, J.: Recent elevation changes of Svalbard glaciers derived from ICESat laser altimetry, Remote Sens. Environ., 114, 2756–2767, https://doi.org/10.1016/j.rse.2010.06.008, 2010b.
Moran, M. L., Greenfield, R. J., Arcone, S. A., and Delaney, A. J.: Delineation of a complexly dipping temperate glacier bed using short-pulse radar arrays, J. Glaciol., 46, 274–286, https://doi.org/10.3189/172756500781832882, 2000.
Nasuti, A., Roberts, D., Dumais, M. A., Stampolidis, A., Ofstad, F., and Kurimo, M.: New high-resolution aeromagnetic and radiometric surveys in Finnmark and North Troms: linking anomaly patterns to geology and structure, Nor. J. Geol., 95, 217–243, https://doi.org/10.17850/njg95-3-10, 2015.
Navarro, F. J., Otero, J., Macheret, Y. Y., Valisenko, E. V., Lapazaran, J. J., Ahlstrøm, A. P., and Machío, F.: Radioglaciological studies on Hurd Peninsula glaciers, Livingston Island, Antarctica, Ann. Glaciol., 50, 17–24, https://doi.org/10.3189/172756409789097603, 2009.
Navarro, F. J., Martín-Español, A., Lapazaran, J. J., Grabiec, M., Otero, J., Vasilenko, E. V., and Puczko, D.: Ice Volume Estimates from Ground-Penetrating Radar Surveys, Wedel Jarlsberg Land Glaciers, Svalbard, Arct. Antarct. Alp. Res., 46, 394–406, https://doi.org/10.1657/1938-4246-46.2.394, 2014.
Ng, F. and Hallet, B.: Patterning mechanisms in subglacial carbonate dissolution and deposition, J. Glaciol., 48, 386–400, https://doi.org/10.3189/172756502781831214, 2002.
Norwegian Polar Institute: Kartdata Svalbard 1:250 000. Sheet 3, Norwegian Polar Institute, 1998.
Ohta, Y.: Recent understanding of the Svalbard basement in the light of new radiometric age determinations, Norsk Geologisk Tidsskrift, 72, 1–5, 1992.
Olaizola, M., van de Wal, R. S. W., Helsen, M. M., and de Boer, B.: An ice flow modeling perspective on bedrock adjustment patterns of the Greenland ice sheet, The Cryosphere, 6, 1263–1274, https://doi.org/10.5194/tc-6-1263-2012, 2012.
Olesen, O., Brönner, M., Ebbing, J., Gellein, J., Gernigon, L., Koziel, J., Lauritsen, T., Myklebust, R., Pascal, C., Sand, M., Solheim, D., and Usov, S.: New aeromagnetic and gravity compilations from Norway and adjacent areas: methods and applications, Geological Society, London, Petroleum Geology Conference series, 7, 559–586, https://doi.org/10.1144/0070559, 2010.
Overrein, Ø., Johansen, B. F., and Dallmann, W. K.: Nordauslandet's geology and landscape, Cruise Handbook for Svalbard, Norwegian Polar Institute, 2015.
Paterson, W. S. B. and Clarke, G. K. C.: Comparison of theoretical and observed temperature profiles in Devon Island ice cap, Canada, Geophys. J., 55, 615–632, https://doi.org/10.1111/j.1365-246X.1978.tb05931.x, 1978.
Phillips, J. D.: Potential-Field Geophysical Software for the PC, version 2.2, USGS open-File Report, 97, https://doi.org/10.3133/ofr97725 1997.
Polteau, S., Hendriks, B. W. H., Planke, S., Ganerød, M., Corfu, F., Faleide, J. I., Midtkandal, I., Svensen, H. S., and Myklebust, R.: The early cretaceous Barents Sea sill complex: distribution, 40Ar/39Ar geochronology, and implications for carbon gas formation, Palaeogeogr. Palaeoclimatol. Palaeoecol., 441, 83–95, https://doi.org/10.1016/j.palaeo.2015.07.007, 2016.
Porter, D. F., Tinto, K. J., Boghosian, A., Cochran, J. R., Bell, R. E., Manizade, S. S., and Sonntag, J. G.: Bathymetric control of tidewater glacier mass loss in northwest Greenland, Earth Planet. Sci. Lett., 401, 40–46, https://doi.org/10.1016/j.epsl.2014.05.058, 2014.
Przylibski, T. A., Ciężkowski, W., Głowacki, T., Grudzińska, K. K., Kasza, D., Zagożdżon, P. P., and Kasza, D.: Front of the Werenskiold Glacier (Svalbard) – changes in years 1957–2013, E3S Web of Conferences, 29, 00030, https://doi.org/10.1051/e3sconf/20182900030, 2018.
Radić, V., Bliss, A., Beedlow, A. C., Hock, R., Miles, E., and Cogley, J. G.: Regional and global projections of twenty-first century glacier mass changes in response to climate scenarios from global climate models, Clim. Dynam., 42, 37–58, https://doi.org/10.1007/s00382-013-1719-7, 2013.
Reid, A. B., Allsop, J. M., Granser, H., Millett, A. J., and Somerton, I. W.: Magnetic interpretation in three dimensions using Euler deconvolution, Geophysics, 55, 80–91, https://doi.org/10.1190/1.1442774, 1990.
Ritzmann, O., Maercklin, N., Faleide, J. I., Bungum, H., Mooney, W. D., and Detweiler, S. T.: A three-dimensional geophysical model of the crust in the Barents Sea region: model construction and basement characterization, Geophys. J. Int., 170, 417–435, https://doi.org/10.1111/j.1365-246x.2007.03337.x 2007.
Salem, A., Williams, S., Fairhead, J. D., Ravat, D., and Smith, R.: Tilt-depth method: A simple depth estimation method using first order magnetic derivatives, The Leading Edge, 26, 1502–1505, https://doi.org/10.1190/1.2821934, 2007.
Schäfer, M., Zwinger, T., Christoffersen, P., Gillet-Chaulet, F., Laakso, K., Pettersson, R., Pohjola, V. A., Strozzi, T., and Moore, J. C.: Sensitivity of basal conditions in an inverse model: Vestfonna ice cap, Nordaustlandet/Svalbard, The Cryosphere, 6, 771–783, https://doi.org/10.5194/tc-6-771-2012, 2012.
Schytt, V.: Some comments on glacier surges in eastern Svalbard, Can. J. Earth Sci., 46, 867–873, https://doi.org/10.1139/e69-088, 1969.
Spector, A.: A gravity survey of the Melville Island ice caps, J. Glaciol., 6, 393–400, https://doi.org/10.3189/s002214300001950x, 1966.
Studinger, M., Bell, R., Fitzgerald, P., and Buck, W.: Crustal architecture of the Transantarctic Mountains between the Scott and Reedy Glacier region and South Pole from aerogeophysical data, Earth Planet. Sci. Lett., 250, 182–199, https://doi.org/10.1016/j.epsl.2006.07.035, 2006.
Studinger, M., Bell, R., and Frearson, N.: Comparison of AIRGrav and GT-1A airborne gravimeters for research applicationsComparison of airborne gravimeters, Geophysics, 73, I51–I61, https://doi.org/10.1190/1.2969664, 2008.
Telford, W. M., Geldart, L. P., and Sheriff, R. E.: Applied Geophysics, 2 ed., Cambridge University Press, Cambridge, 1990.
Thébault, E., Finlay, C. C., Beggan, C. D., Alken, P., Aubert, J., Barrois, O., Bertrand, F., Bondar, T., Boness, A., Brocco, L., Canet, E., Chambodut, A., Chulliat, A., Coïsson, P., Civet, F., Du, A., Fournier, A., Fratter, I., Gillet, N., Hamilton, B., Hamoudi, M., Hulot, G., Jager, T., Korte, M., Kuang, W., Lalanne, X., Langlais, B., Léger, J.-M., Lesur, V., Lowes, F. J., Macmillan, S., Mandea, M., Manoj, C., Maus, S., Olsen, N., Petrov, V., Ridley, V., Rother, M., Sabaka, T. J., Saturnino, D., Schachtschneider, R., Sirol, O., Tangborn, A., Thomson, A., Tøffner-Clausen, L., Vigneron, P., Wardinski, I., and Zvereva, T.: International Geomagnetic Reference Field: the 12th generation, Earth, Planet. Space, 67, 79, https://doi.org/10.1186/s40623-015-0228-9, 2015.
Thompson, D. T.: EULDPH: A new technique for making computer-assisted depth estimates from magnetic data, Geophysics, 47, 31–37, https://doi.org/10.1190/1.1441278, 1982.
Tinto, K. J. and Bell, R. E.: Progressive unpinning of Thwaites Glacier from newly identified offshore ridge: Constraints from aerogravity, Geophys. Res. Lett., 38, L20503, https://doi.org/10.1029/2011gl049026, 2011.
Tinto, K. J., Bell, R. E., Cochran, J. R., and Münchow, A.: Bathymetry in Petermann fjord from Operation IceBridge aerogravity, Earth Planet. Sci. Lett., 422, 58–66, https://doi.org/10.1016/j.epsl.2015.04.009, 2015.
Vaughan, D. G., Comiso, J. C., Allison, I., Carrasco, J., Kaser, G., Kwok, R., Mote, P., Murray, T., Paul, F., Ren, J., Rignot, E., Solomina, O., Steffen, K., and Zhang, T.: Observations: Cryosphere, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 317–382, 2013.
Werner, S.: Interpretation of magnetic anomalies as sheet-like bodies, Sveriges Geologiska Undersökning, Series C, Årsbok, 43, 1955.
Zagorodnov, V. A., Sin'kevich, S. A., and Arkhipov, S. M.: Ice core express-analysis for structure and thermal regime studies of Austfonna, Mater. Glyatsiol. Issled./Data Glaciol. Stud., 66, 149–158, 1989.
Zhao, L., Forsberg, R., Wu, M., Olesen, A. V., Zhang, K., and Cao, J.: A Flight Test of the Strapdown Airborne Gravimeter SGA-WZ in Greenland, Sensors (Basel), 15, 13258–13269, https://doi.org/10.3390/s150613258, 2015.






