2.1 Overview

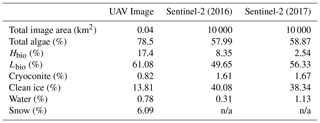
In this study we present a suite of empirical, theoretical and remote-sensing data to quantify and map algal contributions to melting on the south-western GrIS. At our field site we paired spectral reflectance and albedo measurements with removal of surface ice samples for biological and mineralogical analyses in order to quantify the relationship between cell abundance and broadband and spectral albedo. The imaginary part of the refractive index of the local mineral dusts and the purpurogallin-type phenolic compound that dominates absorption in the local glacier algae were measured in the laboratory and incorporated into a new radiative-transfer model. The albedo effects of each impurity were thus examined in isolation and compared. At the same time, we also undertook a sensitivity study with other bulk dust optical properties from previous literature to further test the potential role of mineral dusts in darkening the ice surface. Furthermore, by combining albedo measurements with incoming irradiance spectra and measurements of local melt rates, we estimated the radiative forcing and the proportion of melting that could be attributed to algae in areas of high and low algal biomass (H_bio and L_bio). At our field site we made UAV flights with a multispectral camera in order to map algal coverage at high spatial resolution. We achieved this by training a random-forest (RF) algorithm on our field spectroscopy data to classify the ice surface into discrete categories including H_bio and L_bio. This enabled estimates of algal coverage in a 200 × 200 m area at our field site. We then retrained our classifier for Sentinel-2 satellite imagery and used this to upscale further within the south-western region of the GrIS (to a 100 × 100 km Sentinel-2 tile covering our field site and UAV image area). With these estimates of algal coverage from our remote-sensing imagery and calculations of the proportion of melting attributed to algae from our field data, we were able to estimate runoff attributed to algae using the runoff model by van As et al. (2017). The details of each stage of our methodology are provided in the following Sect. 2.2–2.10.

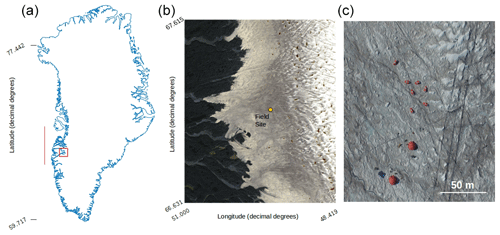
Figure 1(a) Map of Greenland showing the bounding box of the Sentinel-2 tile (22WEV) containing our field site (red box) and the latitudinal extent of our runoff modelling (red line). The basemap was created using the MATLAB Arctic Mapping Toolbox (Greene et al., 2017). The Sentinel-2 tile outlined by the red box is shown in detail in (b) with the field site marked with a yellow dot. Sentinel-2 bands 2, 3 and 4 were combined into a true-colour composite using GDAL (geographical data abstraction library, 2019), by the lead author. Panel (c) shows the area immediately surrounding the field camp as captured by a DJI Phantom Pro by the lead author.

2.2 Field site

Experiments were carried out at the Black and Bloom Project field site (67.04^∘ N, 49.07^∘ W; Fig. 1), near the Institute for Marine and Atmospheric research Utrecht (IMAU) Automatic Weather Station “S6” on the south-western Greenland Ice Sheet between 10 and 22 July 2017. We established a 200×200 m area for UAV mapping (centred on 67.07789444^∘ N, 49.350000^∘ W) where only essential access was allowed (e.g. for placing ground control points, GCPs, for geo-rectifying our UAV images) and sample removal was prohibited. We also delineated an additional adjacent 20 × 200 m area that we referred to as the “sampling strip” in which we made spectral reflectance and albedo measurements paired with removal of samples for biological and mineralogical analyses, as detailed in the following sections. The sampling strip was subdivided into smaller subregions that were then systematically visited each day of our field season. This was necessary because ice surface samples were destructively removed for analysis and this method ensured that each area visited had not been disturbed by our presence on previous days. Some ancillary directional reflectance measurements were also made at the same field site between 15 and 25 July 2016 and appended to our training dataset for supervised classification (Sect. 2.8).

2.3 Field spectroscopy

At each site in our sampling strip, albedo was measured using an ASD (Analytical Spectral Devices, Colorado) Field-Spec Pro 3 spectroradiometer with an ASD cosine collector. The cosine collector was mounted horizontally on a 1.5 m crossbar levelled on a tripod with a height between 30 and 50 cm above the ice surface. The cosine collector was positioned over a sample surface, connected to the spectroradiometer using an ASD fibre optic. Following this, the spectroradiometer was controlled remotely from a laptop, meaning the operators could move away from the instrument to avoid shading it. Two upwards- and two downwards-looking measurements were made in close succession (∼ 2 min) to account for any change in atmospheric conditions, although the measurements presented were all made during constant conditions of clear skies at solar noon ±2 h. Each retrieval was the average of > 20 replicates.

Immediately after making the albedo measurements, the cosine collector was replaced with a 10^∘ collimating lens, enabling a nadir view hemispheric conical reflectance factor (HCRF) measurement to be obtained. For HCRF measurements the upwards-looking measurements were replaced with HCRF measurements of a flat Spectralon^® panel with the spectroradiometer in reflectance mode. This protocol was followed for every sample surface, with both albedo and directional reflectance measurements taking less than 5 min. We closely followed the methodology described by Cook et al. (2017b). Albedo is the most appropriate measurement for determining the surface energy balance, while the HCRF is closer to the measurements made by aerial remote sensing and less sensitive to stray light reflecting from surfaces other than the homogeneous patch directly beneath the sensor. We therefore used the albedo for energy balance calculations and the HCRF for remote-sensing applications in this study.

2.4 Biological measurements

Immediately following the albedo and HCRF measurements, ice from within the viewing area of the spectrometer was removed using a sterile blade and scooped into sterile Whirl-Pak bags, melted in the dark and immediately fixed with 3 % glutaraldehyde. The samples were then returned to the University of Bristol and University of Sheffield where microscopic analyses were undertaken. Samples were vortexed thoroughly before 20 µL was pipetted into a Fuchs–Rosenthal haemocytometer. The haemocytometer was divided into 4 × 4 image areas. These were used to count a minimum of 300 cells to ensure adequate representation of species diversity (where possible, as some low-abundance samples had as few as one cell per haemocytometer). The volume of each image area was used to calculate cells per millilitre. Biovolume was determined by measuring the long and short axes of at least 10 cells from each species in each sample using the measure tool in the GNU Image Manipulation Program (GIMP). The morphology of the cells in the images was used to separate them into two species: Mesotaenium berggrenii and Ancylonema nordenskioldii. These dimensions were then used to calculate the mean volume of each species in each sample, assuming the cells to be circular cylinders (following Hillebrand, 1999, and Williamson et al., 2018). The average volume was multiplied by the number of cells for each species and then summed to provide the total biovolume for each sample.

2.5 Mineral and algal optical properties and radiative-transfer modelling

A new radiative-transfer package, BioSNICAR_GO, was developed for this study and was used to predict the albedo of snow and ice surfaces with algae and mineral dusts. We made a series of major updates and adaptations to the BioSNICAR model presented by Cook et al. (2017b). The package is divided into a bio-optical scheme wherein the optical properties of light-absorbing impurities and ice crystals can be calculated using Mie scattering (for small spherical particles such as black carbon or snow) or geometrical optics (for large and/or aspherical particles such as glacier algae, larger mineral dust particles, and large ice crystals) and a two-stream radiative-transfer model based on SNICAR (Flanner et al., 2007), which incorporates the equations of Toon et al. (1989). A schematic of the model structure is provided in the Supplement (Sect. S1).

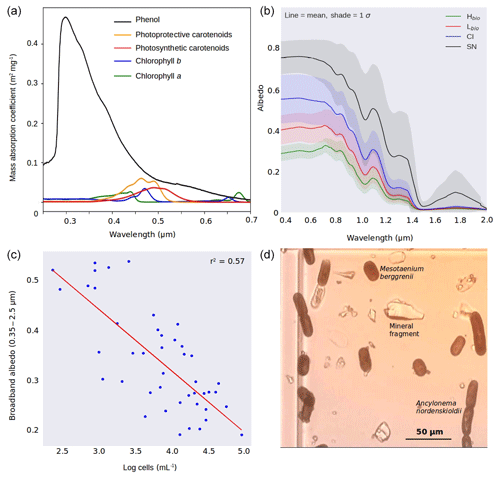
Figure 2(a) Mass absorption coefficients of the major algal pigments including the purpurogallin-type phenol. (b) Measured spectral albedos for each surface type (H_bio is heavy biomass loading, L_bio is light biomass loading, CI is clean ice and SN is snow). (c) Plot showing the natural logarithm of cell abundance against broadband albedo. (d) Microscope image showing examples of both algal species and mineral fragments from a melted H_bio sample.

Download

To incorporate glacier algae into BioSNICAR_GO, geometrical optics were employed to determine the single-scattering optical properties of the glacier algae, since they are large (∼ 10³ µm³, making Mie calculations impractically computationally expensive) and best approximated as circular cylinders (Hillebrand, 1999; Lee and Pilon, 2003). Our approach is adapted from the geometric optics parameterization of van Diedenhoven (2014). The inputs to the geometric optics calculations are the cell dimensions and the complex refractive index. The imaginary part of the refractive index was calculated using a mixing model based upon Cook et al. (2017b), where the absolute mass of each pigment in the algal cells was measured in field samples. The absorption spectra for the algal pigments is provided in Fig. 2a. We updated the mixing model by Cook et al. (2017b) to apply a volume-weighted average of the imaginary part of the refractive index of water and the algal pigments so that the simulated cell looks like water at wavelengths where pigments are non-absorbing. We consider this to be more physically realistic than having cells that are completely non-absorbing at wavelengths > 0.75 µm, especially since a water fraction (X_w) is used in the calculations to represent the non-pigmented cellular components of the total cell volume. This approach also prevents the refractive index from becoming infinite when the water fraction is zero, removing the constraint $\mathrm{0}<X_{\text{w}}<\mathrm{1}$ from the bio-optical scheme in the original BioSNICAR model. Based upon experimental evidence in Dauchet et al. (2015) for the model species C. reinhardii, the real part of the refractive index has been updated from 1.5 (in Cook et al., 2017b) to 1.4. The absorption coefficients from which the imaginary refractive index is calculated are from Dauchet et al. (2015), apart from the purpurogallin-type phenol, whose optical properties were determined empirically (Fig. 2a). The calculated optical properties were added to the lookup library for BioSNICAR-GO for a range of cell dimensions. For the simulations presented in this study, we included two classes of glacier algae representing Mesotaenium berggrenii and Ancylonema nordenskioldii with length and diameter and also the relative abundance of each species matching the means measured in our microscopy described in Sect. 2.4. In simulations (Sect. S2) we found that ice albedo was relatively insensitive to the dimensions of the cells within a realistic range of lengths and diameters. This low sensitivity to cell length and diameter is likely because all of the cells considered here are large from a radiative-transfer perspective.

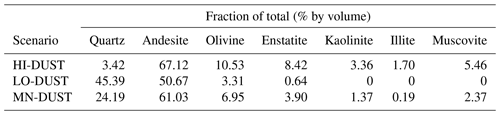
For mineral dusts, we took measured values for surface dust composition and particle size distribution (PSD) obtained at our field site from McCutcheon et al. (2020; hereafter, referred to as McC). We then used complex refractive indices for the appropriate minerals obtained from the existing literature, mixed them using the Maxwell Garnett dielectric mixing approximation according to the measured mass fractions (after converting to volumetric fractions using the mineral densities), generated the single-scattering optical properties using a Mie scattering code and applied a weighted average using the PSD to obtain the bulk optical properties for the dust. Since the mineralogy of the dust varied between sites we generated three dust “scenarios”. In the low-absorption scenario (LO-DUST) all the minerals were set to the minimum volume-fraction measured across all of McC's samples except for quartz, which comprised the remainder. In the high-absorption scenario (HI-DUST) all the minerals were set to their maximum measured volume-fraction, apart from quartz, which comprised the remainder. Finally, in the mean scenario (MN-DUST) all the minerals were present with their volume fractions equal to the mean across all of the field samples. The mineralogy of each of these scenarios is described in Table 1. Refractive indices were not available for all of the individual minerals present in McC's analysis, so we represented the feldspar minerals using the refractive index for andesite (Pollack et al., 1973) and all pyroxenes with the refractive index for enstatite (Jäger et al., 2003), and, in the absence of a refractive index for amphibole phases, we used the refractive index for the similarly green mineral olivine (OCDB, 2002). Refractive indices for all other minerals were available (Rothman et al., 1998; Roush et al., 1991; Pollack et al., 1973; Egan and Hilgeman, 1983; Nitsche and Fritz, 2004).

Table 1Composition of each mineral dust “scenario” in percent of total by volume.

Download Print Version | Download XLSX

The ice optical properties in BioSNICAR-GO were also calculated using a parameterization of geometric optics adapted from van Diedenhoven et al. (2014). A geometrical optics approach to generating ice optical properties was chosen because it enables arbitrarily large ice grains with a hexagonal columnar shape to be simulated, in order to better estimate the albedo of glacier ice where grains are large and aspherical. While the real ice surface is composed of irregularly shaped and sized grains, this approach enabled us to simulate our field spectra much more accurately and circumvented the requirements that individual grains be small and spherical in the case of the Lorenz–Mie approach. The optical properties of the ice grains were modelled using refractive indices from Warren and Brandt (2008). The radiative-transfer model is a two-stream model described in full in Cook et al. (2017b) and Flanner et al. (2007). For the radiative-transfer modelling presented in this study, the following model parameters were used: diffuse illumination; ice crystal side-length and diameter per vertical layer = 3, 4, 5, 8, and 10 mm; layer thicknesses = 0.1, 1, 1, 1 and 1 cm; underlying surface albedo = 0.15; and layer densities = 500, 500, 600, 600 and 600 kg m⁻³. These ice physical properties were chosen to reduce the absolute error between the simulated albedo for ice without any impurities (“clean ice”) and our mean field-measured clean-ice spectrum.

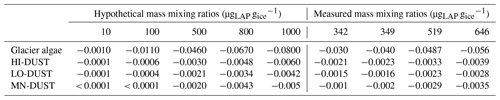
To realistically simulate measured dust and algal mass loadings on the ice surface, we took measured values for H_bio field samples. For mineral dusts we took the mean and maximum mineral mass mixing ratios from McC. They measured 394±194 µg_LAP mL_ice⁻¹, of which ∼ 95 % was inorganic, giving mean and maximum mineral dust loadings of 373 and 567 µg_LAP mL_ice⁻¹. Assuming 1 mL of ice to weigh 0.917 g, this gives mean and maximum mass mixing ratios of 342 and 519 µg_dust g_ice⁻¹. For glacier algae we calculated mass mixing ratios by taking the mean cell volume across all cells in our microscope images, converting to per-cell mass using a constant cell density (0.87 g cm⁻³; Hu, 2014) and multiplying by our mean and maximum H_bio cell abundance. This gave mean and maximum mass mixing ratios of 349 and 646 µg_algae g_ice⁻¹. We also varied the mass mixing ratios over a range of hypothetical values to study the sensitivity of ice surface albedo to dust and glacier algae. Glacier algae and each of the mineral dusts (LO-DUST, HI-DUST, MN-DUST) were added individually to the upper 0.1 cm layer in mixing ratios of 10, 100, 500 and 1000 µg_LAP g_ice⁻¹, plus the mean and maximum measured mass mixing ratios for dust and algae, to quantify their effects on the surface albedo. We also ran a sensitivity study where we repeated the simulations with two other dust types, sourced from previous literature, with contrasting mineralogies to our field site.

2.6 Empirical measurement of mineral dust reflectance

For two samples of local mineral dusts obtained from H_bio sites, we chemically removed the organic matter and measured the PSD using scanning electron microscopy (full details in Sect. S3). The chemical cleaning method avoided the artificial “reddening” of the mineral dust sample associated with removing organic matter by ignition. We then arranged the mineral dust samples into an optically thick layer on a microscope slide and pressed them tightly against the open aperture of a Thorlabs IS200-4 integrating sphere to measure their reflectance. The other apertures were covered with SM05CP2C caps and the sample reflectance was measured using the same ASD Field Spec Pro 3 as was used for field measurements.

2.7 Radiative forcing and biological melt acceleration

The biological radiative forcing was calculated by first differencing the albedo for algal surfaces and the albedo for clean ice surfaces measured at our field site. This gives the difference in albedo between the clean and algal ice surfaces, α_diff. The product of each α_diff and the incoming irradiance, I^*, provided the instantaneous power density (PD_alg) absorbed by the algae. We assume that photosynthetic processes utilize 5 % of this absorbed energy – at the upper end of a realistic range for photosynthetic microalgae (Blankenship et al., 2011; Masojídek et al., 2013). The remainder of PD_alg is conducted into the surrounding ice, giving the instantaneous radiative forcing due to algae (IRF_alg). Since these cells are coloured by the purple purpurogallin pigment, we assume the reflective radiative forcing to be negligible, as demonstrated by Dial et al. (2018). IRF_alg was calculated at hourly intervals using incoming irradiance simulated for our field site using the PVSystems solar irradiance program (https://pvlighthouse.com.au, last access: July 2019) at 1 nm spectral resolution, following Dial et al. (2018). The radiative forcing was assumed to be constant between each 1 h time step, meaning the radiative forcing over 1 h (HRF_alg) could be calculated by multiplying IRF_alg by 3600 s h⁻¹, assuming that instantaneous radiative forcing is equal to radiative forcing per second. Daily radiative forcing due to algae (RF_alg) was then calculated as the sum of HRF_alg between 00:00 and 23:00 UTC.

To calculate the algal contribution to melting (M_alg), IRF_alg was multiplied by 10⁴ to convert the radiative forcing from units of W m⁻² to W cm⁻² and then divided by the latent heat of fusion for melting ice (334 J g⁻¹) and integrated over the entire day as described above. This provided a value for the amount of melting caused by the presence of algae per day assuming the cold content of the ice to be depleted. We calculated uncertainty by running these calculations for every possible combination of our measured algal and clean ice spectra and calculating the mean, standard error, and standard deviation of the pooled results.

We corroborated these estimates using a point surface energy balance model (Brock and Arnold, 2000; Tedstone, 2019). This model predicts melting in millimetres of water equivalent given local meteorological data and information about the ice surface albedo and roughness. We ran this model with the albedo set equal to the broadband albedo for each clean ice (CI), heavy biomass (H_bio) and light biomass (L_bio) spectrum in our field measurements. The hourly meteorological data for 21 July 2017 used to force the model were from a Delta-T GP1 automatic weather station positioned at our field site. The difference in predicted melt between the algal surfaces and the clean ice surfaces provided the melt attributed to the presence of algae. As for the radiative forcing calculations, the uncertainty was calculated by running the energy balance model for every possible combination of algal and clean ice spectra and calculating the mean, standard error, and standard deviation of the pooled results.

2.8 UAV and Sentinel-2 remote sensing

Having quantified algal melt acceleration in localized patches using the methods described in Sect. 2.2–2.6, we then used a multispectral camera mounted to a UAV to quantify algal coverage across a 200 × 200 m area at our field site. This sample area was kept pristine throughout the study period to minimize artefacts of our presence appearing in the UAV imagery. Inside the sampling area we placed fifteen 10 × 10 cm ground control points (GCPs), whose precise location was measured using a Trimble differential GPS. At these markers we also made ground spectral measurements using an ASD-Field Spec Pro 3 immediately after each flight. The UAV itself was a Steadidrone Mavrik-M quadcopter, onto which we integrated a MicaSense Red-Edge multispectral camera. The camera is sensitive in five discrete bands, with centre wavelengths of 475, 560, 668, 717, and 840 nm and bandwidths of 20, 20, 10, 10, and 40 nm, respectively. The horizontal field of view was 47.2^∘ and the focal length 5.4 mm. The camera was remotely triggered through the autopilot, which was programmed along with the flight coordinates in the open-source software Mission Planner (Osborne, 2019). Images were acquired at approximately 2 cm ground resolution with 60 % overlap and 40 % sidelap. The flights were less than 20 min long and at an altitude of 30 m above the ice surface.

We applied radiometric calibration and geometric distortion correction procedures to acquired imagery following MicaSense procedures (Micasense, 2019). We then converted from radiance to reflectance using time-dependent regression between images of the MicaSense Calibrated Reflectance Panel acquired before and after each flight (i.e. a regression line was computed between the reflectance of the white reference panel at the start and end of the flight and used to quantify the change in irradiance during the flight). Finally, the individual reflectance-corrected images were mosaicked using AgiSoft PhotoScan following procedures developed by the United States Geological Survey (USGS, 2017), yielding a multi-spectral ortho-mosaic with 5 cm ground resolution, georectified to our GCPs. There was generally close agreement between the ground, UAV and satellite-derived albedo, although there are some differences that we believe to be the result of different radiometric calibration techniques for satellite, UAV and ground measurements, and the differing degrees of spatial integration have been examined in detail in Tedstone et al. (2019).

To upscale further, we used multispectral data from the Copernicus Sentinel-2 satellite. We selected the 100 × 100 km tile covering our field site (T22WEV) on the closest cloud-free day to our UAV flight on 21 July. The L1C product was downloaded from SentinelHub (Sinergise, Slovenia). The L1C product was processed to L2A using the European Space Agency (ESA) Sen2Cor processor, including atmospheric correction and reprojection to 20 m resolution.

2.9 Supervised classification algorithms and albedo mapping

To map and quantify spatial coverage of algae over the ice sheet surface we employed a supervised classification scheme. A random forest (RF) classifier was trained on the field spectra collected on the ice surface (see Sect. 2.3) and then applied to multispectral images gathered by the UAV and Sentinel-2. We also included spectra obtained at the same field site in July 2016 to our training set, giving a total of 231 labelled spectra. A schematic of the classification workflow is provided in Sect. S4. Our HCRF measurements were first reduced to reflectance values at five key wavelengths coincident with the centre wavelengths measured by the MicaSense Red-Edge camera mounted to the UAV (blue: 0.475; green: 0.560; red: 0.668; red edge: 0.717; NIR: 0.840 µm), yielding reflectance at each wavelength as a feature vector for the classifier (in this case the spectral response function of the camera was not accounted for). The classification labels were the surface type as determined by visual inspection: SN (snow), CI (clean ice), CC (cryoconite), WAT (water), L_bio (low-biomass algae) and H_bio (high-biomass algae). For the algal surface classes our visual assessment was corroborated by microscopy, as described in Sect. 2.2. This dataset was then shuffled and split into a training set (80 %) and a test set (20 %). The training set was used to train three individual supervised classification algorithms: Naive Bayes, k-nearest neighbours (KNN) and support vector machine (SVM). For the SVM, the parameters C and gamma were tuned using grid search cross validation. Two ensemble classifiers were also trained: a voting classifier that combined the predictions of each of the three individual classifiers and a RF algorithm. The performance of each classifier was measured using precision, accuracy, recall, and F1 score and also by plotting the confusion matrix and normalized confusion matrix for each classifier. In all cases the RF outperformed the other classifiers according to all available metrics (Sect. S5). The performance of the RF classifier was finally measured on the test set, demonstrating the algorithm's ability to generalize to unseen data outside of the training set. Overfitting is not usually associated with the RF classifier, and the strong performance on both our training and test sets confirms that the model generalizes well. For these reasons, we used the RF algorithm to classify our multispectral UAV and Sentinel-2 images. Training the classifier using data from field spectroscopy ensures the quality of each labelled data point in the training set, since our sampling areas were homogeneous and surface samples were analysed in the laboratory, circumventing issues of spatial heterogeneity and uncertainty in labelling that could lead to ambiguity for direct labelling of aerial images. Comparisons between the directional reflectance spectra gathered using the ASD field spectrometer and those measured using the UAV and Sentinel-2 are provided in Fig. 3. Simultaneously with the surface classification, we calculated the albedo in each UAV pixel using the narrowband to broadband conversion of Knap et al. (1999) applied to the reflectance at each of the five bands.

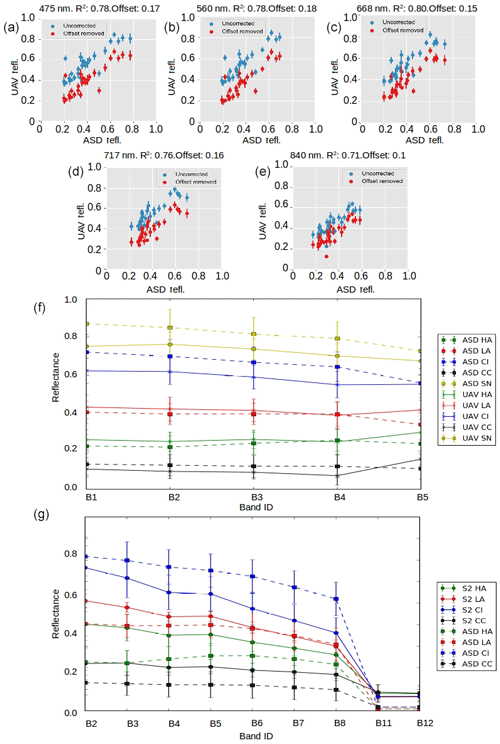
Figure 3Inter-sensor comparisons. (a–e) Each UAV band reflectance plotted against ASD reflectance in uncorrected (blue) and corrected (red) form. The correction was applied to account for a systematic offset shown in the header for each plot. (f) Mean reflectance and ±1 standard deviation error bars at each spectral band for each surface class for the ASD field spectrometer and the UAV-mounted multispectral camera. (g) Mean reflectance and ±1 standard deviation error bars at each spectral band for each surface class for the ASD field spectrometer and Sentinel-2.

Download

This protocol was repeated for Sentinel-2 imagery. Additional bands are available for use as feature vectors in the case of Sentinel-2. Directional reflectance data gathered using the ASD field spectrometer were reduced to only those nine wavelengths coincident with the centre wavelengths measured by Sentinel-2 at 20 m ground resolution (0.480, 0.560, 0.665, 0.705, 0.740, 0.788, 0.865, 1.610, 2.190 µm). Training on reduced hyperspectral data has several advantages over training directly on aerial multispectral data. First, the method is sensor agnostic because the classifier can be retrained with a different selection of wavelengths for other upscaling platforms, enhancing the reusability of the field measurements. Second, we have confidence in our labels because each sample has been analysed in a laboratory to confirm its composition, reducing label ambiguity. Finally, the limited field of view of the field spectrometer reduces errors arising from mixing of spectra from heterogeneous ice surfaces. Sentinel-2 imagery was masked using the MeASUREs Greenland Ice Mapping Project ice mask (Howat, 2017) to eliminate non-ice areas. Pixels with more than 30 % probability of being obscured by cloud were masked using the Sentinel-2 L2A cloud product generated by the Sen2Cor processor. For the calculation of albedo in each pixel, the additional bands available in the Sentinel-2 images enabled the application of Liang et al.'s (2001) narrowband to broadband conversion.

2.10 Comparing 2016 and 2017

In 2017, the GrIS dark zone had a relatively small spatial extent, high albedo and short duration in comparison to the other years in the MODIS record, particularly since 2007, whereas the dark zone was especially dark, widespread and prolonged in 2016 (Fig. 4; Tedstone et al., 2017). We therefore conducted a comparison between the algal coverage on the same dates in 2016 and 2017. First, we examined variations in the extent and duration of the dark zone, along with snow depths and snow clearing dates for the south-western ablation zone using MODIS, extending the time series of Tedstone et al. (2017). Bare ice was mapped by applying a threshold reflectance value (R<0.60 at 0.841–0.871 µm) to the MOD09GA Daily Land Surface Reflectance Collection 6 product. Within the bare-ice area, dark ice was mapped using a lower reflectance threshold (R<0.45 at 0.62–0.67 µm). The area of interest was the “common area” defined by Tedstone et al. (2017) bounded within the latitudinal range 65–70^∘ N and is equal to that used by Wang et al. (2018). To measure the annual dark-ice extent (in km²) we counted the pixels that were dark for at least 5 d each year. The annual duration was defined at each pixel as the percentage of daily cloud-free observations made in each JJA (June–July–August) period that were classified as dark. The timing of bare ice appearance was calculated from MODIS using a rolling window approach on each pixel (see Tedstone et al., 2017). The mean snow depths were extracted from outputs from the regional climate model MAR v3.8 (Fettweis et al., 2017) run at 7.5 km resolution forced by ECMWF ERA-Interim reanalysis data (Dee et al., 2011). These data enabled a comparison of the extent and timing of dark ice in 2016 and 2017.

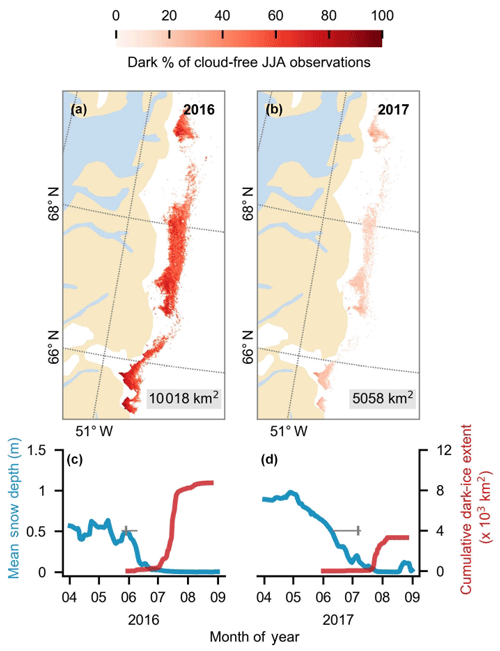
Figure 4(a, b) Dark-ice duration on the south-western GrIS in summers 2016 and 2017, expressed as a percentage of the total daily cloud-free observations made during June–July–August (JJA). Each year is labelled with dark-ice extent. In each year, pixels that are dark for fewer than 5 d are not shown. (c, d) Average snow depth modelled by MAR (blue) and cumulative dark-ice extent observed by MODIS (red) (Tedstone et al., 2017) during April to August. Vertical bars (grey) denote median date of snow clearing derived from MODIS. Horizontal bars denote the interquartile range of the day of year of bare ice appearance. Tick marks denote the start of each month.

To examine algal coverage in each year we identified the Sentinel-2 tile covering our field site (22WEV) on the closest cloud-free date to the UAV flight day (21 July) in each year. These were 26 July 2017 and 25 July 2016. Since we were interested in the bare-ice zone, snow-covered pixels were omitted from the calculations.

2.11 Runoff modelling

Runoff at the regional scale was calculated using van As et al.'s (2017) surface mass balance (SMB) model, forced with local automatic weather station and MODIS albedo observations (van As et al., 2012, 2017). The model interpolates meteorological and radiative measurements from three PROMICE automatic weather stations on the K-transect (KAN-L, KAN-M and KAN-U) and bins them into 100 m elevation bands (0 to 2000 m a.s.l.). Surface albedo is from MODIS Terra MOD10A1 albedo and is averaged into the same 100 m elevation bins. For every 1 h time step, the model iteratively solves the surface energy balance for the surface temperature. If energy components cannot be balanced due to the 0 ^∘C surface temperature limit, a surplus energy sink for melting of snow or ice is included. If surface temperature is greater than the melting point, the surplus energy is used for melting of snow or ice. When calculating turbulent heat fluxes, aerodynamic surface roughness for momentum was set to 0.02 and 1 mm for snow and ice, respectively (after van As et al., 2005, 2012; Smeets and Van den Broeke, 2008). We extrapolate modelled runoff across the south-western GrIS (65–70^∘ N) by deriving the areas of each elevation bin using the Greenland Ice Mapping Project (GIMP) digital elevation model (DEM; Howat et al., 2014). Total summer runoff from bare ice was calculated by summing runoff in elevation bins that had mean daily albedo of less than 0.60. Total summer runoff from dark ice only was calculated in the same way but using a 0.39 threshold. The study by van As et al. (2017) compared the performance of the model with independent observations and found errors to be negligible in the bare-ice zone.

To determine the algal contribution to runoff, we used Eq. (1):

where R_alg is the runoff due to algae, R_tot is the total runoff from the bare-ice zone calculated using our runoff model, $M_{H_{\text{bio}}}$ and $M_{L_{\text{bio}}}$ are the mean percentage of total melt attributed to algae in H_bio and L_bio areas as calculated by our energy balance modelling described in Sect. 2.6, and C${}_{H_{\text{bio}}}$ and $C_{L_{\text{bio}}}$ are the proportion of C_tot comprised of H_bio and L_bio areas in our UAV or Sentinel-2 images. As discussed later, the Sentinel-2 algal coverage estimate is conservative because it often fails to resolve H_bio surfaces and therefore provides a lower bound on the runoff attributed to algae. An upper bound was therefore also calculated by assuming the spatial coverage derived from our UAV remote sensing – which can accurately distinguish L_bio and H_bio – surfaces is representative of the south-western dark zone. We were thereby able to estimate upper and lower limits for the runoff attributed to algal growth on the south-western ablation zone.

3.1 Algae reduce ice albedo

The ice surfaces we studied were divided into four classes depending upon the algal abundance measured in the melted ice samples: high algal abundance (H_bio), low algal abundance (L_bio), clean ice (CI) and snow (SN). The algal abundance (cells mL⁻¹) in each class was as follows: $H_{\text{bio}}=\mathrm{2.9}\times {\mathrm{10}}^{\mathrm{4}}\pm \mathrm{2.01}\times {\mathrm{10}}^{\mathrm{4}}$; $L_{\text{bio}}=\mathrm{4.73}\times {\mathrm{10}}^{\mathrm{3}}\pm \mathrm{2.57}\times {\mathrm{10}}^{\mathrm{3}}$; CI $=\mathrm{625}\pm \mathrm{381}$; and SN $=\mathrm{0}\pm \mathrm{0}$ (1 SD). These cell abundances were significantly different between the classes (one-way ANOVA: F=10.21; $p=\mathrm{3}\times {\mathrm{10}}^{-\mathrm{5}}$), which Bonferroni-corrected t tests indicated to be due to variance between all four groups. The dominant species of algae were Mesotaenium berggrenii and Ancylonema nordenskioldii (Fig. 2d), confirming observations made by Stibal et al. (2017) and Williamson et al. (2018) in the same region. Their long, thin and approximately cylindrical morphology has been shown to be near-optimal for light absorption (Kirk, 1976). The albedo of the ice surface also varied significantly between the surface classes (one-way ANOVA for broadband albedo: F=7.9; $p=\mathrm{2.8}\times {\mathrm{10}}^{-\mathrm{4}}$), again with Bonferroni-corrected t tests showing variance between all four groups (Sect. S6a, b). Greater algal abundance was associated with lower albedo, with the albedo reduction concentrated in the visible wavelengths (Fig. 2b) where both solar energy receipt and algal absorption peak (Cook et al., 2017b; Williamson et al., 2018), diminishing towards longer near infra-red (NIR: > 0.70 µm) wavelengths where ice absorption, represented by the effective grain size, is most likely to cause albedo differences (Warren, 1982). A strong inverse correlation (Pearson's R=0.75, $p=\mathrm{2.74}\times {\mathrm{10}}^{-\mathrm{9}}$) was observed between the natural logarithm of algal cell abundance (cells mL⁻¹) in the surface ice samples and broadband albedo (Fig. 2c). The linear regression coefficient of determination between the albedo and the natural logarithm of cell abundance was 0.57. It is unsurprising that the cell abundance does not account for all variation in albedo because there are also albedo-reducing effects related to the physical structure of the ice and presence of melt water (as demonstrated for snow by, for example, Warren, 1982). An inverse relationship was also observed between broadband albedo and biovolume (calculated as the sum of the products of the mean measured cell volumes and the cell counts for each algal species), but the coefficient of determination was lower (r²=0.42). This may well be the result of larger cells having a smaller effect on albedo than more numerous, smaller cells for a given total volume. The relationship between absorption and scattering coefficients and cell size may also not be straightforward for algal cells due to an increasingly important contribution to the cell optical properties from internal heterogeneity, organelles, cell walls and the pigment packaging effect in larger cells (Morel and Bricaud, 1981; Haardt and Maske, 1987).

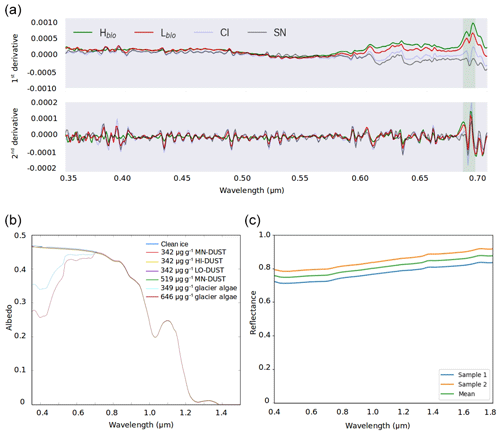
Figure 5(a) The first and second derivative spectra for each surface class. (b) BioSNICAR-GO modelled spectral albedo for clean ice (blue) and ice with each of the simulated local dusts and algae in their measured mass mixing ratios in the upper 1 mm. (c) Reflectance for an optically thick layer of two samples of the local mineral dust.

Download

The albedo of H_bio and L_bio surfaces is depressed in the visible wavelengths (0.40–0.70 µm, Fig. 2b), creating a red-edge spectrum commonly used in other environments as a marker for photosynthetic pigments (Seager et al., 2005) and for mapping algae over the GrIS by Wang et al. (2018). Chlorophyll a has a specific absorption feature at 0.68 µm which is hard to discern in the raw spectra but clear in the derivative spectra (Fig. 5a) for H_bio and L_bio but not CI and SN. This feature has previously been described as “uniquely biological” (Painter et al., 2001) and supports the hypothesis that the albedo reduction observed in these samples is primarily due to algae. Our measurements therefore strongly indicate a biological role in reducing the albedo of the GrIS surface; however, to test that the lower broadband and spectral albedo observed on algal surfaces is primarily due to the presence of algal cells, it was also necessary to compare the albedo-reducing effects of the algae to that of local mineral dust.

Table 2Albedo change relative to clean ice caused by the addition of each LAP to the upper 1 mm of ice in a range of mass mixing ratios from 10 to 1000 µg_LAP g_ice⁻¹.

Download Print Version | Download XLSX

3.2 Algae have greater impact on albedo than mineral dust

Radiative-transfer simulations demonstrated that at measured mass mixing ratios mineral dusts only have a very small (< 0.003) albedo-reducing effect at our field site on the south-western GrIS, whereas glacier algae reduce the ice albedo by up to 0.06, not accounting for indirect albedo-reducing feedbacks. The effect of adding the mean measured mass mixing ratio of MN-DUST to the clean ice was a very small albedo reduction of 0.002 (Table 2; Fig. 5b). In contrast, adding the mean measured mass mixing ratio of glacier algae reduced the albedo by 0.03, preferentially in the short visible wavelengths in a similar way to our field-measured reflectance spectra (Table 2; Fig. 5b). This effect was greater when the mass mixing ratio was increased to the maximum measured values (646 µg_algae g_ice⁻¹ and 519 µg_dust g_ice⁻¹) which caused an albedo reduction of 0.06 for glacier algae and 0.003 for MN-DUST. Changing the proportions of the minerals in our simulated local dusts had a very small effect on the albedo reduction. At the mean measured mass mixing ratio, HI-DUST reduced the albedo by just 0.0023, while LO-DUST reduced the albedo by 0.0016. Even with a mass mixing ratio of 1000 µg_dust g_ice⁻¹, the albedo reduction due to local mineral dusts was only 0.006, 0.004 and 0.005 for the HI-DUST, LO-DUST and MN-DUST, compared to 0.08 for glacier algae.

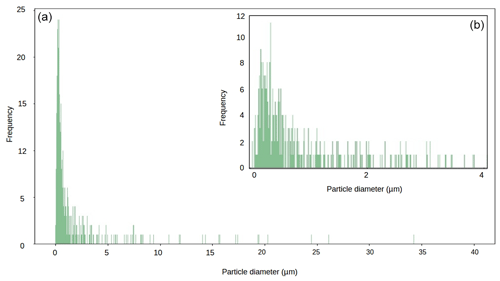
Figure 6Particle size diameter for our local mineral dust sample (panel (b) shows magnification of 0–4 µm range).

Download

Across all our simulations, the broadband albedo-reducing power of glacier algae exceeded that of the local mineral dusts, often by several orders of magnitude. At field-measured mass mixing ratios for heavily laden H_bio surfaces, mineral dusts cannot account for the broadband albedo reduction observed in the field. This is consistent with the local mineralogy being dominated by weakly absorbing minerals with small grain sizes, as measured in our field sample (Figs. 5c, 6; Table 2). In Sect. S7 we demonstrate that these conclusions are robust to different dust types, including those with typically Saharan optical properties and dusts with varying hematite concentrations. The radiative-transfer simulations do not account for feedbacks related to grain size and shape, near-surface meltwater accumulation, and the presence of other light absorbing particles, such as humic substances, that might modify the spectral reflectance and exacerbate the biological albedo reduction. Furthermore, the albedo-lowering effects of both the glacier algae and mineral dusts is reduced by the low albedo of the underlying ice. In simulations using smaller diameter, higher-albedo snow grains (whose optical properties were estimated using Mie theory) the albedo reduction caused by 1000 µg_dust g_ice of MN-DUST increased to 0.009, 0.010 and 0.012 for grains of diameter 1500, 1000 and 500 µm, respectively.

The small direct albedo-reducing effect from local minerals on the ice surface is seemingly in contrast to some previous studies, such as Wientjes et al. (2010, 2011) and Bøggild (2010); however, we highlight that neither of the Wientjes et al. (2010, 2011) studies directly measured the surface albedo or any optical properties of the mineral dusts retrieved from their GrIS sampling sites and only inferred mineralogical darkening from low spectral resolution MODIS data and the presence of a “wavy pattern” observed across the dark zone. We argue that while this may be indicative of geological outcropping onto the ablation zone, it does not necessarily follow that these minerals are responsible for surface darkening. In support of this, Wientjes et al. (2011) found strongly scattering and weakly absorbing quartz to be the dominant mineral in surface ice and speculated that biota may be having a darkening effect. Bøggild et al. (2010) found mineral dust to be an albedo reducer in Crown Prince Christian Land (80^∘ N, 24^∘ W), but this area is geologically and climatologically distinct from our field site and their transect only spanned ∼ 8 km from the ice sheet margin, being an area prone to local dust deposition. Overall, our study is consistent with previous studies that have identified that the local bare-ice mineral dust is poor in hematite and rich in weakly absorbing quartz and feldspar minerals (e.g. Tedesco et al., 2013). Tedesco et al. (2013) reported their dusts being redder than algae. However, their minerals were sourced from cryoconite, not the ice surface, where glacier algae are scarce and the biota is dominated by a rich consortium of other microbes that lack the characteristic pigmentation of glacier algae. Furthermore, Tedesco et al. (2013) reported an average of only 0.3 % goethite in their Greenland cryoconite samples. This may have been present as hematite prior to their sample processing, which involved heating the samples to 500–1000 ^∘C. This heating treatment likely oxidized Fe-bearing mineral phases, thereby artificially introducing the observed reddening.

While these radiative-transfer simulations indicate that mineral dust is unlikely to be directly causing the albedo decline on the GrIS, they may still influence the ice albedo indirectly by acting as substrates for the formation of low-albedo microbial mineral aggregates known as cryoconite granules, which are often found in quasi-cylindrical melt holes or scattered over ice surfaces (Wharton et al., 1985; Cook et al., 2015a) or by providing a nutrient source stimulating algal growth (Stibal et al., 2017). This is especially true because there is evidence in the previous literature that the dust present on the GrIS bare-ice surface is likely derived from a local source with no contribution from Asian dusts or volcanic ash (Wientjes et al., 2011) and that red minerals such as hematite, goethite and ilmenite are present only in very low concentrations (Wientjes et al., 2011; Tedesco et al., 2013; Sanna and Romeo, 2018) that would have a negligible effect on the ice albedo.

Therefore, we have demonstrated using empirical measurements and radiative-transfer modelling that glacier algae are potent albedo reducers on the south-western Greenland Ice Sheet and mineral dusts are not. These findings are consistent with several previous studies (Stibal et al., 2017; Yallop et al., 2012) that found mineral dust to be insignificant for explaining albedo variations in the same region.

3.3 Indirect effects of algae

Algae predominantly reduce the ice albedo in the visible wavelengths (0.40–0.70 µm), whereas variations in the NIR result mainly from changes to ice grain radii and the presence of liquid water (Warren, 1982; Green et al., 2002). Variations in the NIR albedo between the surface classes therefore suggest that the lower albedo of algal surfaces is not explained entirely by enhanced absorption due to algae but also by the smoother, wetter ice surface with fewer opportunities for high-angle scattering of photons (Jonsell et al., 2003) compared to the well-drained and porous CI surfaces. The spatial and temporal development of the weathering crust is therefore an important control on ice albedo (Muller and Keeler, 1969; Jonsell et al., 2003). Algal growth is stimulated by melt, which can be enhanced by algal growth (Yallop et al., 2012; Ganey et al., 2017; Stibal et al., 2017; Cook et al., 2017a, b; Dial et al., 2018) – an example of a bio-cryomorphic process where biota alter the physical, chemical and hydrological conditions of the ice surface with beneficial consequences to the biota (Cook et al., 2015b).

3.4 Algae enhance radiative forcing and melt

Having determined that glacier algae reduce the ice surface albedo, we took an empirical approach to quantifying their impact upon energy balance following Ganey et al. (2017), which includes both direct albedo effects (enhanced absorption of shortwave solar radiation by the algal cells) and the indirect effects explained above. Integrated over the entire day, this indicated a daily mean biological radiative forcing of 116 and 65 W m⁻² for H_bio and L_bio surfaces, respectively, similar to RFs for Alaskan snow algae calculated by Ganey et al. (2017). We used the biological radiative forcing integrated over the entire day and the latent heat of fusion for ice (334 J cm⁻³) to estimate 1.35±0.01 (standard error, SE) cm w.e. of melting due to algae in H_bio areas on 21 July. For L_bio sites, biological melting on 21 July 2017 was 1.01±0.01 (SE) cm w.e.

We corroborated this estimate using a point surface energy balance model (Brock and Arnold et al., 2000). The melt attributed to the presence of algae predicted by the energy balance modelling method was similar to that predicted using the radiative forcing method, with 1.37±0.48 (SE) cm w.e. attributed to H_bio and 0.95±0.41 (SE) cm w.e. attributed to L_bio. Expressing the melt attributed to algae as a proportion of the total melting in the algal sites gives 26.15±3.77 % (SE) of the local melting attributed to algae in the H_bio surfaces and 21.62±5.07 % (SE) for L_bio surfaces.

Table 3Summary of the albedo for each surface class as predicted from our classified UAV image, the Sentinel-2 image for 2016 (S2 2016) and 2017 (S2 2017), and as measured using field spectroscopy (ASD Field Spec) at our field site in 2017 (we do not have cosine collector albedo measurements for water or cryoconite surfaces). The reported values are the mean, the standard deviation in brackets and the number of observations.

Download Print Version | Download XLSX

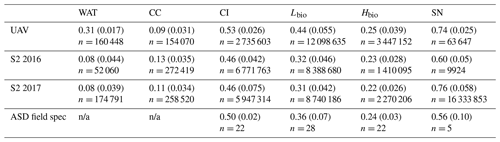
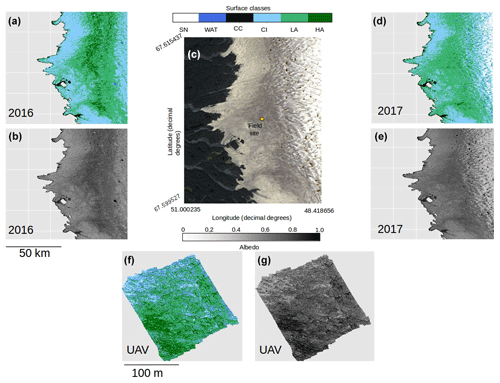
Figure 7(a) Classified map of the area shown in (c) for 2016. (b) Broadband albedo map of the area shown in (c) for 2016. (c) RGB “true colour” image showing the Sentinel-2 tile covering our field site in the Kangerlussuaq area. (d) Classified map of the area shown in (c) for 2017. (e) Broadband albedo map of the area shown in (c) for 2017. (f) Classified map of a 200 × 200 m area at the field site marked in (c) imaged using a UAV-mounted multispectral camera. (g) Broadband albedo map of a 200 × 200 m area at the field site marked in (c) imaged using a UAV-mounted multispectral camera. Panels (a–e) all have pixel resolution of 20 m and use the base geographic coordinate reference system WGS84 and the Universal Tranvserse Mercator Projection (UTM) 22N. The scale bar beneath (b) is common to (a, b, d, e), and the scale bar beneath (f) is common to (f) and (g).

Table 4Percentage of each image covered by each surface type as predicted by our trained RF algorithm. Snow was removed from the calculation in the Sentinel-2 images to enable quantification of surface coverage in the bare-ice zone, i.e. below the snow line, only.

Download Print Version | Download XLSX

3.5 Algae are widespread across the south-western ablation zone

Our analyses demonstrate that algae have a dramatic darkening effect on the ice surface, leading to increased melting. However, the importance of this effect depends upon the spatial extent of the algal blooms over thousands of kilometres. To determine spatial coverage at our field site we classified multispectral images acquired from a UAV flown over a 200 × 200 m area. The classified UAV image indicated that 78.5 % of the area was covered by algal blooms, of which 61.1 % was L_bio and 17.4 % was H_bio (Table 3; Fig. 7). The high ground resolution of the imagery enabled a qualitative assessment of the algorithm performance by visual comparison between the classifier and the raw imagery (following Ryan et al., 2018a). The algorithm produced qualitatively realistic bloom shapes, correctly placed water in channels and individual cryoconite holes in their correct positions. The confusion matrix indicates that occasional misclassifications are generally between water and cryoconite (Sect. S8). This is unsurprising since both cryoconite and water have relatively flat spectral shapes with few spectral features and cryoconite is often found beneath pools of surface water. We also point out that our cryoconite spectral reflectance measurements were made with cryoconite filling the entire field of view of the spectrometer and thus best represent large cryoconite holes or dispersed cryoconite rather than surfaces peppered with many small holes. There was also some ambiguity between thin, wet snow and bare glacier ice, as these surfaces are spectrally similar. Nevertheless, these misclassifications affect a small area of the pixel and do not affect our estimate of algal bloom coverage.

We also classified Sentinel-2 satellite data (Fig. 7). The confusion matrices (Sect. S8) indicate similar misclassification types and frequencies to the UAV model. The predicted algal coverage was 58.87 %. H_bio surfaces were much less common than L_bio (H_bio=2.53 %; L_bio=56.54 %; Table 3). The spatial coverage by algae was different in the Sentinel and UAV datasets especially for H_bio, likely because (a) the Sentinel-2 imagery includes ice that is outside of the dark zone, raising the overall reflectivity, and (b) even in the UAV image, which was retrieved from within the dark zone, H_bio surfaces comprise just 17 % of the ice surface and have a patchy distribution. The lowest-albedo surfaces – cryoconite and water – cover a small fraction (< 3 %) of the total area in both UAV and Sentinel-2 images (Table 4), although we note that many individual cryoconite holes will not be detected as they are smaller than the spatial resolution of either Sentinel-2 or the UAV. The spatial coverage reported here from our multispectral UAV imagery is consistent with a k-nearest neighbours classification scheme applied to RGB (red, green, blue) imagery from a fixed wing UAV flight over the Kangerlussuaq region by Ryan et al. (2018a). They found up to 85 % of the ice surface to be composed of “ice containing uniformly distributed impurities” in the same region of the dark zone in July 2014, which our observations confirm were dominated by algae. They also found < 2 % of the ice surface to be cryoconite-covered and that water coverage was < 5 % (except for a supraglacial lake in their imaged area). This analysis demonstrates that algae are a major component of the ice surface. The larger spatial coverage of algae observed in UAV images compared to Sentinel-2 images likely results from spatial integration occurring at the coarser spatial resolution associated with Sentinel-2 data, where pixels are likely to be classified as CI unless the majority of the pixel is covered by algae. Smaller H_bio patches are rarely detected, presumably because they are unlikely to cover the majority of a 20 m pixel. The higher detection limit for algae with decreasing ground resolution makes our estimate of spatial coverage from Sentinel-2 conservative. We highlight that this will have a much larger effect on studies aiming to quantify cell abundance using Sentinel-3 where the ground resolution is 300 m.

3.6 Algae reduce the ice albedo across the south-western ablation zone

There was a significant difference between the albedos of each surface class in all four datasets, consistent with the findings from our ground spectroscopy (Table 4). The albedo of each surface class is approximately consistent between the datasets, despite the variation in spatial coverage, giving confidence in the accuracy of our remote-sensing albedo retrievals and the classification algorithm. In the expansive areas where algae are present (Fig. 7), the ice albedo is on average 0.13 lower for L_bio and 0.25 lower for H_bio compared to clean ice (Table 4). This, combined with our ground-based spectroscopy, radiative forcing calculations, and radiative-transfer and energy balance modelling, provides robust evidence in support of algae having a significant melt-accelerating effect on the GrIS. We cannot yet explicitly separate mineral and biological effects, but our theoretical and empirical analyses indicate that (a) local mineral dust cannot explain the observed albedo reduction, (b) low-albedo areas had significantly elevated algal cell numbers relative to clean ice, (c) uniquely biological features were detectable in the spectra and derivative spectra for the lower-albedo sites, and (d) radiative-transfer models incorporating algal cells with realistic pigment profiles demonstrate the mechanism of albedo reduction. These observations confirm that supervised classification of H_bio and L_bio surfaces is indeed detecting surfaces with high algal loading and can be used to estimate algal bloom extent. Again, we point out that this estimate is conservative because there is certain to be glacier algae present in low numbers in some of the areas that are classified as clean and H_bio patches are often smaller than the ground resolution of Sentinel-2, raising their detection limit (Tedstone et al., 2019). Furthermore, these calculations consider the total albedo-reducing effect, inclusive of ice structure and meltwater feedbacks, not only the direct light-absorbing effects of the algal biomass.

3.7 Algae cause enhanced GrIS runoff

We ran a SMB model forced with local automatic weather station and MODIS albedo observations (van As et al., 2012) to estimate 45.5 Gt runoff from all bare ice and 33.8 Gt from dark ice in 2017. We used the mean spatial coverage determined using our remote sensing in each year and our radiative forcing calculations that attributed 21.62±5.07 (SE) % of melting to algae in L_bio sites and 26.15±3.77 (SE) % in H_bio sites to generate estimates for the GrIS runoff caused by algal growth. We have provided upper and lower estimates based on our two remote-sensing datasets because, while our UAV is able to accurately map H_bio and L_bio surfaces, we cannot be certain that the spatial coverage derived from the 200 × 200 m area is representative of the south-western dark zone. At the same time, our Sentinel-2 remote sensing underestimates algal coverage because it includes ice outside of the dark zone and H_bio patches are often too small to be resolved at 20 m pixel resolution (Tedstone et al., 2019). Therefore, we used the spatial coverage determined by our Sentinel-2 classification as a lower bound and spatial coverage determined by our UAV classification as an upper bound on our estimate of total runoff attributed to the presence of algae.

We found that in 2017 between 4.4 and 6.0 Gt of ice loss could be attributed to the growth of algae, representing 10 %–13 % of the total runoff from the south-western GrIS, with the lower estimate generated using algal coverage from Sentinel-2 and the upper estimate generated using spatial coverage at our field site from our UAV. When the calculations were restricted to the dark zone only (i.e. excluding areas in the ablation zone not classified as “dark”), algal contributions to total runoff were up to 18 %. These calculations confirm that algal growth is an important factor in the contribution of the GrIS to global sea level rise. This contribution will increase if biologically darkened areas expand or a greater proportion of the ice is covered by high-biomass blooms under warmer climates. These observations therefore indicate that the omission of biological growth is leading current models to underestimate future GrIS contributions to sea level rise.

3.8 Interannual variability and potential positive feedback

MODIS data (Fig. 4) indicate that 2017 was a particularly high-albedo year when the dark zone was especially small and bright, whereas 2016 was a particularly low-albedo year where the dark zone was wider and darker than most years (Fig. 4a and b and Tedstone et al., 2017). Previous field evidence (Williamson et al., 2018) demonstrates that the ice was darkened by high concentrations of algae in 2016. In our Sentinel-2 remote-sensing tile (22WEV) the bare-ice zone was wider in 2016 (6758 km²) than in 2017 (6205 km²) and a larger area was covered with algae (on 25 July 2016, 3919 km² was covered by algae compared to 3653 km² on 28 July 2017). While the proportional total algal coverage was similar between the 2 years (57.99 % in 2016 and 58.87 % in 2017), the proportion of the algal ice that was classified H_bio was much higher in 2016 (8.35 %) compared to 2017 (2.54 %). The mean albedos and their standard deviations were very similar for each ice surface class in both years (Table 4). The runoff from the south-western GrIS bare ice (albedo < 0.6) was 94.1 Gt in 2016, of which 67.6 was from dark ice (albedo < 0.39). We estimate that 8.8–12.2 Gt of this runoff was attributable to the growth of algae, representing 9 %–13 % of the total runoff from bare-ice sectors. The absolute values for runoff are therefore much higher but the proportion of the bare-ice total attributed to algae was approximately the same between the 2 years.

The snow line retreated further and earlier in 2016 compared to 2017, creating a wider bare-ice zone that existed for longer and was not transiently covered by summer snowfall events, whereas in 2017 a smaller bare-ice area was exposed later and was covered by 5–10 cm of snow several times during the summer (Fig. 4c, d). The more prolonged exposure of a larger bare-ice zone in 2016 enabled L_bio surfaces to extend to higher elevations and biomass to accumulate to greater mass concentrations at lower elevations in summer 2016, explaining the greater H_bio coverage. This indicates that the intensity of the algal bloom is a function of exposure time, as postulated by Tedstone et al. (2017) and Williamson et al. (2018). More prolonged exposure of larger ablation areas under a warming climate (Stroeve et al., 2013; Shimada et al., 2016; Tedesco et al., 2016; Tedstone et al., 2017) are likely to be prone to more spatially expansive, darker algal blooms that enhance melt rates, leading to a potential positive feedback that is not currently accounted for in surface mass balance models, whereby earlier exposure of bare ice leads to enhanced algal coverage, which will be able to accumulate higher biomass and accelerate melting. Melting in turn stimulates algal growth by liberating nutrients and liquid water.