the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Modelling last glacial cycle ice dynamics in the Alps
Julien Seguinot
Susan Ivy-Ochs
Guillaume Jouvet
Matthias Huss
Martin Funk
Frank Preusser
The European Alps, the cradle of pioneering glacial studies, are one of the regions where geological markers of past glaciations are most abundant and well-studied. Such conditions make the region ideal for testing numerical glacier models based on simplified ice flow physics against field-based reconstructions and vice versa.
Here, we use the Parallel Ice Sheet Model (PISM) to model the entire last glacial cycle (120–0 ka) in the Alps, using horizontal resolutions of 2 and 1 km. Climate forcing is derived using two sources: present-day climate data from WorldClim and the ERA-Interim reanalysis; time-dependent temperature offsets from multiple palaeo-climate proxies. Among the latter, only the European Project for Ice Coring in Antarctica (EPICA) ice core record yields glaciation during marine oxygen isotope stages 4 (69–62 ka) and 2 (34–18 ka). This is spatially and temporally consistent with the geological reconstructions, while the other records used result in excessive early glacial cycle ice cover and a late Last Glacial Maximum. Despite the low variability of this Antarctic-based climate forcing, our simulation depicts a highly dynamic ice sheet, showing that Alpine glaciers may have advanced many times over the foreland during the last glacial cycle. Ice flow patterns during peak glaciation are largely governed by subglacial topography but include occasional transfluences through the mountain passes. Modelled maximum ice surface is on average 861 m higher than observed trimline elevations in the upper Rhône Valley, yet our simulation predicts little erosion at high elevation due to cold-based ice. Finally, despite the uniform climate forcing, differencesin glacier catchment hypsometry produce a time-transgressive Last Glacial Maximum advance, with some glaciers reaching their modelled maximum extent as early as 27 ka and others as late as 21 ka.
For nearly 300 years, montane people and early explorers of the European Alps learned to read the geomorphological imprint left by glaciers in the landscape and to understand that glaciers had once been more extensive than today (Windham and Martel, 1744). Contemporaneously, it was also observed in the Alps that glaciers move by a combination of meltwater-induced sliding at the base (de Saussure, 1779) and viscous deformation within the ice body (Forbes, 1846). As glaciers flow and slide across their bed, they transport rock debris and erode the landscape, thereby leaving geomorphological traces of their former presence. In the mid-nineteenth century, more systematic studies of glacial features showed that Alpine glaciers extended well outside their current margins (Venetz, 1821) and even onto the Alpine foreland (de Charpentier, 1841), yielding the idea that, under colder temperatures, expansive ice sheets had once covered much of Europe and North America (Agassiz, 1840).
However, this glacial theory did not gain general acceptance until the discovery and exploration of the two present-day ice sheets on Earth – the Greenland and Antarctic ice sheets – provided a modern analogue for the proposed European and North American ice sheets. Although it was long unclear whether there had been single or multiple glaciations, this controversy ended with the large-scale mapping of two distinct moraine systems in North America (Chamberlin, 1894). In the European Alps, the systematic classification of the glaciofluvial terraces on the northern foreland later indicated that there had been at least four major glaciations in the Alps (Penck and Brückner, 1909). More recent studies of glaciofluvial stratigraphy in the foreland indicate at least 15 Pleistocene glaciations (Ivy-Ochs et al., 2008; Preusser et al., 2011; Schlüchter, 1988).
From the mid-twentieth century, palaeo-climate records extracted from deep sea sediments and ice cores have provided a much more detailed picture of the Earth's environmental history (Augustin et al., 2004; Dansgaard et al., 1993; Emiliani, 1955; Shackleton and Opdyke, 1973), indicating several tens of glacial and interglacial periods. During the last 800 kyr (thousand years before present), these glacial cycles have succeeded each other with a periodicity about 100 ka (Augustin et al., 2004; Hays et al., 1976). Nevertheless, this global signal is largely governed by the North American and Eurasian ice sheet complexes. It is thus unclear whether glacier advances and retreats in the Alps were in pace with global sea-level fluctuations. Besides, the landform record is typically sparse throughout time and, more often, spatially incomplete. Palaeo-ice sheets did not leave a continuous imprint on the landscape, and much of this evidence has been overprinted by subsequent glacier re-advances and other geomorphological processes (Kleman, 1994; Kleman et al., 2006, 2010). Dating uncertainties typically increase with age, such that dated reconstructions are strongly biased towards later glaciations (Heyman et al., 2011). In the European Alps, although sparse geological traces indicate that the last glacial cycle may have comprised two or three cycles of glacier growth and decay (Ivy-Ochs et al., 2008; Preusser, 2004), most glacial features currently left on the foreland present a record of the last major glaciation of the Alps, dating from the Last Glacial Maximum (Ivy-Ochs, 2015; Monegato et al., 2017; Wirsig et al., 2016).
The spatial extent and thickness of Alpine glaciers during the LGM, an integrated footprint of thousands of years of climate history and glacier dynamics, have been reconstructed from moraines and trimlines across the mountain range (Bini et al., 2009; Castiglioni, 1940; Coutterand, 2010; Penck and Brückner, 1909; van Husen, 1987). The assumption that trimlines, the upper limit of glacial erosion, represent the maximum ice surface elevation has been repeatedly invalidated in other glaciated regions of the globe (Ballantyne and Stone, 2015; Fabel et al., 2012; Kleman, 1994; Kleman et al., 2010). Although no evidence for cold-based glaciation has been reported in the Alps to date, it is supported by numerical modelling (Blatter and Haeberli, 1984; Cohen et al., 2018; Haeberli and Schlüchter, 1987). Alpine ice flow patterns were primarily controlled by subglacial topography, but there is evidence for flow across major mountain passes (Coutterand, 2010; Kelly et al., 2004; van Husen, 2011) and self-sustained ice domes (Bini et al., 2009). Finally, the timing of the LGM in the Alps (Ivy-Ochs et al., 2008; Monegato et al., 2017) is in good agreement with the maximum expansion of continental ice sheets recorded by marine oxygen isotope stage (MIS) 2 (Lisiecki and Raymo, 2005). Regional variation between different piedmont lobes exists (Wirsig et al., 2016), but it is unclear whether this relates to climate or glacier dynamics (Monegato et al., 2017), uncertainties in the dating methods, or both.
Although the glacial history of the European Alps has been studied for nearly 300 years, uncertainties remain on (1) what climate evolution led to the known maximum ice limits, (2) what extent ice flow was controlled by subglacial topography, (3) what drove the different responses of the individual lobes, (4) how far above the trimline the ice surface was located, and (5) how many advances occurred during the last glacial cycle.
Here, we intend to explore these open questions from a new angle and use the Parallel Ice Sheet Model (the PISM authors, 2015), a numerical ice sheet model that approximates glacier sliding and deformation (Sect. 2), to model Alpine glacier dynamics through the last glacial cycle (120–0 ka), a period for which palaeo-temperature proxies are available, albeit non-regional. In an attempt to analyse the long-standing questions outlined above, we test the model sensitivity to multiple palaeo-climate forcings (Sect. 3) and then explore the modelled glacier dynamics at high resolution for the optimal forcing (Sect. 4). Additional geological research will be needed to complete our knowledge.
2.1 Overview
We use the Parallel Ice Sheet Model (development version e9d2d1f), an open-source, finite-difference, shallow ice sheet model (the PISM authors, 2015). The model requires input on initial bedrock and glacier topographies, geothermal heat flux, and climate forcing. It computes the evolution of ice extent and thickness over time, the thermal and dynamic states of the ice sheet, and the associated lithospheric response. The model set-up used here was previously developed and tested on the Cordilleran ice sheet (Seguinot, 2014; Seguinot et al., 2014, 2016) and subsequently adapted for a steady climate (Becker et al., 2016) and regional (Becker et al., 2017; Jouvet et al., 2017a) applications to the European Alps.
Ice deformation follows a temperature- and water-content-dependent creep formulation (Sect. 2.2). Basal sliding follows a pseudo-plastic law where the yield stress accounts for till dilatation under high water pressure (Sect. 2.3). Bedrock topography is deflected under the ice load (Sect. 2.4). Surface mass balance is computed using a positive degree-day (PDD) model (Sect. 2.5). Climate forcing is provided by a monthly climatology from interpolated observational data (Hijmans et al., 2005) and the European Centre for Medium-Range Weather Forecasts Reanalysis Interim (Dee et al., 2011), which is amended with temperature lapse-rate corrections (Sect. 2.6), time-dependent temperature offsets, and in some cases, time-dependent palaeo-precipitation reductions (Sect. 3).
Each simulation starts from assumed present-day ice thickness and equilibrium temperature in the ice and bedrock at 120 ka and runs to the present. Our modelling domain of 900 by 600 km encompasses the entire Alpine range (Fig. 1). The simulations were run on two different grids, using horizontal resolutions of 2 and 1 km. All parameter values are summarized in Table 1.
2.2 Ice rheology
Ice sheet dynamics are typically modelled using a combination of internal deformation and basal sliding. PISM is a shallow ice sheet model, which implies that the balance of stresses is approximated based on their predominant components. The shallow shelf approximation (SSA) is combined with the shallow ice approximation (SIA) by adding velocity solutions of the two approximations (Winkelmann et al., 2011). In the SIA, topographic roughness is parametrized using a bed smoother range of 5 km (Schoof, 2003). Although the SSA–SIA heuristic is inaccurate in the transition zone where both vertical shear and longitudinal stretch are significant, it was shown to effectively approximate complex ice sheet flow dynamics over mountainous topographies similar to that of the European Alps (Golledge et al., 2012; Ziemen et al., 2016).
Ice deformation is governed by the constitutive law for ice (Glen, 1952; Nye, 1953). Ice softness depends on ice temperature, pressure, and water content through an enthalpy scheme (Aschwanden et al., 2012). It follows a piecewise Arrhenius-type rheology representative of Holocene polar ice (Cuffey and Paterson, 2010) and increases with liquid water fractions up to 0.01 (Cuffey and Paterson, 2010; Duval, 1977; Lliboutry and Duval, 1985), an arbitrary threshold above which new ice deformation measurements are critically needed (Kleiner et al., 2015).
Surface air temperature derived from climate forcing (Sects. 2.6, 3.1) provides the upper boundary condition to the ice enthalpy model. Temperature is computed in the ice and in the bedrock down to a depth of 3 km below the glacier base, where it is conditioned by a lower boundary geothermal heat flux estimate from multiple geothermal proxies (Goutorbe et al., 2011; Fig. 1a).
2.3 Basal sliding
A pseudo-plastic sliding law relates the bed-parallel shear stresses to the sliding velocity. The yield stress is modelled using the Mohr–Coulomb criterion (Tulaczyk et al., 2000), using a constant basal friction angle corresponding to the average of available measurements (Cuffey and Paterson, 2010). Effective pressure is related to the ice overburden stress and the modelled amount of subglacial water, using a formula derived from laboratory experiments with till extracted from the base of Ice Stream B in West Antarctica (Bueler and van Pelt, 2015; Tulaczyk et al., 2000). Basal meltwater is accumulated locally without horizontal transport. When the till becomes saturated, additional meltwater is assumed to drain instantaneously and is removed from the system in an accountable way. Other parameters (Table 1) follow simulations of the Greenland ice sheet (Aschwanden et al., 2013) or benchmarks when other data are missing (Bueler and van Pelt, 2015).
2.4 Basal topography
The initial basal topography is bilinearly interpolated from the hole-filled Shuttle Radar Topography Mission (SRTM) data with a resolution of 30 arcsec (Jarvis et al., 2008). These data include post-glacial sediment fills and lake surface topography. However, they were corrected for an estimation of present-day ice thickness based on modern glacier outlines, surface topography, and simplified ice physics (Huss and Farinotti, 2012).
Basal topography responds to ice load following a bedrock deformation model that includes local isostasy, elastic lithosphere flexure, and viscous asthenosphere deformation in an infinite half-space (Bueler et al., 2007; Lingle and Clark, 1985). Model parameters were set according to results from glacial isostatic adjustment modelling of deglacial rebound in the Alps, most closely reproducing observed modern uplift rates (Mey et al., 2016).1
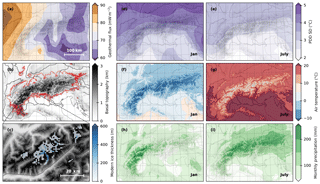
Figure 1(a) Geothermal heat flow from applying the similarity method to multiple geophysical proxies (Goutorbe et al., 2011) used as a boundary condition to the bedrock thermal model 3 km below the ice–bedrock interface. (b) Initial basal topography from SRTM (Jarvis et al., 2008) and geomorphological reconstruction of Last Glacial Maximum Alpine glacier extent (Ehlers et al., 2011). (c) Extract from the estimated present-day ice thickness (Huss and Farinotti, 2012) subtracted from the SRTM topography and aggregated to a 1 km horizontal resolution. (d) Modern January and (e) July standard deviation (Seguinot, 2013) of daily mean temperature from the ERA-Interim (Dee et al., 2011) monthly climatology approximating temperature variability. (f) Modern January and (g) July mean near-surface air temperature, and (h) January and (i) July precipitation from WorldClim (Hijmans et al., 2005) used to compute surface mass balance. The background maps contain Natural Earth data (Patterson and Kelso, 2017).
2.5 Surface mass balance
Ice surface accumulation and ablation are computed from monthly mean near-surface air temperature, Tm, monthly standard deviation of near-surface air temperature, σ, and monthly precipitation, Pm, using a temperature-index model (Hock, 2003). Accumulation is equal to precipitation when air temperatures are below 0 ∘C and decreases to zero linearly with temperatures between 0 and 2 ∘C. Ablation is computed from PDD, the integral of temperatures above 0 ∘C.
The PDD computation accounts for stochastic temperature variations by assuming a normal temperature distribution with standard deviation, σ, around the expected value, Tm. It is expressed by an error-function formulation (Calov and Greve, 2005), which is numerically approximated using week-long subintervals. In order to account for the effects of spatial and seasonal variations in temperature variability (Seguinot, 2013), σ is computed from ERA-Interim daily temperature values from 1979 to 2012 (Mesinger et al., 2006), including variability associated with the seasonal cycle (Seguinot, 2013), and bilinearly interpolated to the model grids (Fig. 1d and e). Degree-day factors for snow and ice melt are set to values used in the European Ice Sheet Modelling INiTiative (Huybrechts, 1998).
2.6 Reference climate forcing
The climate forcing driving the ice sheet simulations consists spatially of a present-day monthly mean climatology, {Tm0,Pm0}, modified by a temperature lapse-rate correction, ΔTLR, temperature offset time series, ΔTTS, and time-dependent palaeo-precipitation corrections, ΨPP:
The present-day monthly mean climatology was bilinearly interpolated from near-surface air temperature and precipitation rate fields from WorldClim (Hijmans et al., 2005), which is representative of the period 1960 to 1990. The modern climate of the European Alps is characterized by a north–south gradient in winter and summer air temperatures (Fig. 1f and g) and an east–west gradient in winter precipitation (Fig. 1h), which is reversed in summer (Fig. 1i). WorldClim data were selected as an input to the ice sheet model because they incorporate observations from the dense weather station network of central Europe (Hijmans et al., 2005). Besides, WorldClim data were previously used as climate forcing for PISM to model the LGM extent of the former Cordilleran ice sheet in good agreement with geological evidence along the southern margin (Seguinot et al., 2014) where weather station density is lower than in the Alps. Finally, the last glacial cycle Alpine glaciers did not extend over marine areas where WorldClim data are missing.
The temperature lapse-rate corrections, ΔTLR, are computed as a function of ice surface elevation, s, using the SRTM-based topography data provided with WorldClim as a reference, bref:
thus accounting for the evolution of ice thickness, , on the one hand, and for differences between the basal topography of the ice flow model, b, and the WorldClim reference topography, bref, on the other hand. All simulations use an annual temperature lapse rate of , which is slightly above annual lapse rates measured in the Alps but more representative of summer months when surface melt occurs (Rolland, 2003).
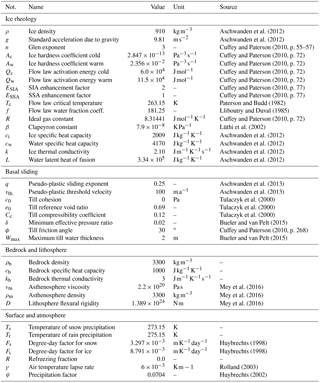
Aschwanden et al. (2012)Aschwanden et al. (2012)Paterson and Budd (1982)Lliboutry and Duval (1985)Lüthi et al. (2002)Aschwanden et al. (2012)Aschwanden et al. (2012)Aschwanden et al. (2012)Aschwanden et al. (2012)Aschwanden et al. (2013)Aschwanden et al. (2013)Tulaczyk et al. (2000)Tulaczyk et al. (2000)Tulaczyk et al. (2000)Bueler and van Pelt (2015)Bueler and van Pelt (2015)Mey et al. (2016)Mey et al. (2016)Mey et al. (2016)Huybrechts (1998)Huybrechts (1998)Rolland (2003)Huybrechts (2002)Table 1Parameter values used in the ice sheet model. Symbols refer to equations used by Seguinot (2014) and Seguinot et al. (2016).
In this section, we analyse the model sensitivity to palaeo-climate forcing through the last glacial cycle, using three palaeo-temperature records (Sect. 3.1) and two parametrizations of palaeo-precipitation (Sect. 3.2), in terms of modelled evolution of total ice volume (Sect. 3.3) and glaciated area during MIS 2 and 4 (Sect. 3.4).
These simulations use a horizontal resolution of 2 km. The vertical grid consists of 31 temperature layers in the bedrock and up to 126 enthalpy layers in the ice, corresponding to vertical resolutions of 100 and 40 m, respectively.
3.1 Palaeo-temperature forcing
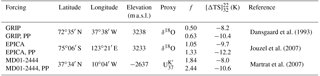
Dansgaard et al. (1993)Jouzel et al. (2007)Martrat et al. (2007)Table 2Palaeo-temperature proxy records and scaling factors yielding temperature offset time series used to force the ice sheet model through the last glacial cycle (Fig. 2). f corresponds to the scaling factor adopted to yield Last Glacial Maximum ice limits in the vicinity of mapped end moraines (Fig. 3a), and refers to the resulting mean temperature anomaly during the period 32 to 22 ka after scaling.
Only few regional proxy records exist that extend over periods when the Alps were glaciated (Heiri et al., 2014). These include lake sediment records in the north and west of the Alps (Duprat-Oualid et al., 2017; Wohlfarth et al., 2008; de Beaulieu and Reille, 1992) and cave speleothems in the Eastern (Boch et al., 2011; Spötl and Mangini, 2002) and Western (Luetscher et al., 2015) Alps. Due to the scarcity of vegetation north of the Alps during glacial periods, varying sources for moisture advection, and the limited duration of the records, quantitative palaeoclimatic interpretation will require both combining multiple proxies in space and time, and comparing them against regional circulation model output (Heiri et al., 2014).
In our simulations, temperature offset time series, ΔTTS, are derived from distal palaeo-temperature proxy records from the Greenland Ice Core Project (Dansgaard et al., 1993), the European Project for Ice Coring in Antarctica (Jouzel et al., 2007), and an oceanic sediment core from the Iberian margin (Martrat et al., 2007). Palaeo-temperature anomalies from the GRIP record are calculated from the oxygen isotope (δ18O) measurements using a quadratic equation (Johnsen et al., 1995),
while temperature reconstructions from the EPICA and MD01-2444 records are provided as such. For each proxy record used and each of the parameter set-ups used in the sensitivity tests, palaeo-temperature anomalies are scaled linearly (Table 2, Fig. 2a) so that, within a 150×100 km rectangular domain covering the Rhine glacier piedmont lobe (Fig. 3a, black rectangle), the modelled cumulative glaciated area during MIS 2 (29–14 ka) is consistent with the glaciated area of the geological reconstruction (Ehlers et al., 2011).
3.2 Palaeo-precipitation forcing
Finally, in some simulations (hereafter labelled PP), precipitation was reduced with air temperature in order to simulate the potential rarefaction of atmospheric moisture in colder climates. This was done using an empirical relationship derived from observed accumulation rates and oxygen isotope concentrations in the GRIP ice core (Dahl-Jensen et al., 1993),
with (Huybrechts, 2002). The control simulations use constant precipitation, corresponding to ψ=0. This simple relationship does not reflect the complexity of atmospheric circulation changes that governed moisture availability over the Alps during the last glacial cycle. Palaeo-climate proxies indicate slightly reduced LGM precipitation in western Europe with anomalies diminishing eastwards (Wu et al., 2007). Regional circulation models indicate generally dryer conditions during MIS 3 (Barron and Pollard, 2002; Kjellström et al., 2010) but more precipitation south of the Alps during MIS 2 (Ludwig et al., 2016; Strandberg et al., 2011). Besides, changes in the ice surface topography may have redistributed orographic precipitation.
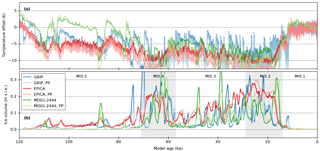
Figure 2(a) Temperature offset time series from ice core and ocean records (Table 2) used as palaeo-climate forcing for the ice sheet model. (b) Modelled total ice volume through the last 120 thousand years (ka) expressed in metres of sea-level equivalent (m s.l.e.). Shaded grey areas indicate the timing for MIS 2 and MIS 4 (Lisiecki and Raymo, 2005). The simulation driven by the EPICA temperature yields smaller ice volume variability and a more realistic timing of deglaciation.
3.3 Sensitivity of ice volume evolution
For the three palaeo-temperature records and the two palaeo-precipitation parametrizations used, the model yields significant ice volume build-up during MIS 4 and 2 (Fig. 2b), corresponding to documented glaciation periods in the Alps (Ivy-Ochs et al., 2008; Preusser, 2004). All simulations also yield important glaciations during MIS 5 and 3, but their timing and amplitude varies significantly depending on the climate forcing used. All six simulations overestimate the late-glacial re-advance during the Younger Dryas (Ivy-Ochs et al., 2009). This is partly because the 2 km resolution used in these simulations is too coarse to resolve Younger Dryas Alpine glaciers. However, the large total ice volume overestimation resulting from the GRIP temperature forcing (Fig. 2b, blue curves) certainly indicates that the vigorous cooling experienced during the Younger Dryas in Greenland is not representative of the Alps.
Geological data from the best documented Alpine piedmont lobes indicate that their maximum extension during MIS 2 occurred around 25.5–24.0 ka (Monegato et al., 2017), after which Alpine glaciers remained or potentially re-advanced to within close reach of this maximum extent, until as late as 22 to 17 ka (Ivy-Ochs, 2015; Wirsig et al., 2016). The EPICA simulations yield an early maximum ice volume at 25.2/24.6 (without/with palaeo-precipitation reductions), followed by a retreat and then a standstill until 17.3 ka (Fig. 2b, red curves) in a very good agreement with these geological data. On the other hand, the simulations forced by the GRIP palaeo-temperature record yield two distinct total ice volume maxima at 27.3/27.0 and 21.8/21.7 ka followed by an early deglaciation of the foreland by 21.4 ka. The MD01-2444 palaeo-temperature forcing yields a late LGM peak ice volume at 16.5/15.7 ka followed by a rapid retreat, in contrast to dated records of large-scale ice retreat by 17 to 16 ka (Ivy-Ochs et al., 2006, 2008).
Finally, all simulations yield very strong ice volume variability over the last 120 kyr (Fig. 2b), indicative of many more than the two or three documented cycles of glacier advance and retreats onto the foreland for this time period (Ivy-Ochs et al., 2008; Preusser, 2004). Palaeo-precipitation reductions dampen some of the small-scale variability, but they have little effect on the millennial scales that characterize those cycles (Fig. 2b, light colour curves). In particular, strong millennial variability recorded in GRIP δ18O (Dansgaard–Oeschger events) has large repercussions on the modelled Alpine ice volume, including around six glaciations of LGM magnitude (Fig. 2b, blue curves), which are not supported by geologic evidence (Ivy-Ochs et al., 2008; Preusser, 2004). Dansgaard–Oeschger events, however, have been recorded in European lake sediments (Wohlfarth et al., 2008) and cave speleothems (Luetscher et al., 2015; Spötl and Mangini, 2002). Our results indicate that their magnitude in Europe was likely smaller than that recorded in GRIP δ18O, which either implies smaller associated palaeo-temperature fluctuations in Europe than in Greenland, or temperature-independent controls on GRIP δ18O. In contrast, the EPICA palaeo-temperature record has the smallest variability among the records used (Fig. 2a, red curves). This results in smaller variability in the total ice volume and more restrictive glaciations during MIS 5 and 3 (Fig. 2b, red curves).
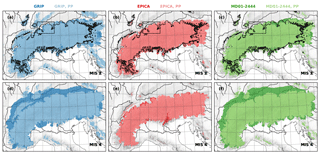
Figure 3(a–c) Modelled maximum ice extent during MIS 2 (29–14 ka), without (dark colours) and with (light colours) palaeo-precipitation corrections, and using temperature time-series scaling factors (Table 2) adjusted to model the area glaciated by the Rhine glacier piedmont lobe (black rectangle) in agreement with the Last Glacial Maximum (LGM) geomorphological reconstruction (Ehlers et al., 2011). (d–f) Modelled maximum ice extent during MIS 4 (71–57 ka). Only the simulation driven by the EPICA temperature time series yields realistic MIS 4 ice cover.
3.4 Sensitivity of glaciated area
During MIS 2, all six simulations yield comparative modelled maximum extents (Fig. 3a). This result is inherent to the palaeo-climate forcing approach used, which involves a linear scaling of each palaeo-temperature anomaly record to a geomorphological reconstruction of the area glaciated by the Rhine Glacier piedmont lobe (Sect. 3.1; Fig. 3a, black rectangle). Outside this benchmark area, all simulations underestimate ice extent in the western part of the model domain and overestimate it in the eastern part, relative to the geomorphological ice limits (Fig. 3a). This result might indicate that the LGM temperature depression, here taken as homogeneous, was actually lower in the Eastern Alps than in the Western Alps, as previously shown by positive degree-day modelling of the central European palaeo-ice caps (Heyman et al., 2013). Alternatively, the east–west gradient in winter precipitation existing today (Fig. 1h) was perhaps enhanced during the LGM, as indicated by pollen reconstructions (Wu et al., 2007). The LGM extent of Alpine glaciers might have been affected by an east–west gradient in variables not accounted for by the PDD model, such as cloud cover or dust deposition. Finally, modern precipitation data from WorldClim also bear uncertainties and exhibit local disagreement with other regional data (Isotta et al., 2013).
Besides this general pattern, there exist differences in glaciated area depending on the palaeo-climate forcing used. The MD01-2444, and to a greater extent the GRIP palaeo-temperature records, tend to overestimate MIS 2 ice cover on all peripheral ranges that surround the Alps (Fig. 3a and c). This is particularly true when no precipitation corrections are applied (bright colours). In fact, both palaeo-temperature records have a larger temperature variability and contain brief spells of cold temperatures (Fig. 2b, blue and green curves), which are too short to develop a fully grown Alpine ice sheet, but long enough to build up ice cover on a smaller scale in these peripheral ranges. On the other hand, peripheral glaciation modelled using the EPICA record (Fig. 3b), which has smaller temperature variability, is in relatively good agreement with the geomorphological reconstructions.
The modelled extent of glaciation during MIS 4 depicts a more pronounced sensitivity to the choice of palaeo-climate forcing used. Using the GRIP and MD01-2444 palaeo-temperature records, Alpine glaciers are modelled to extend well beyond the reach of documented LGM end-moraines (Fig. 3d and f). Because, in both cases, the modelled glaciation extent corresponds to brief cold spells in the palaeo-temperature forcing (Fig. 2a), palaeo-precipitation reductions greatly reduce the excessive modelled ice cover (Figs. 2b and 3d and f, light colours). However, with or without palaeo-precipitation corrections, the GRIP and MD01-2444 forcing yield modelled ice extents (Fig. 3d and f) and volumes (Fig. 2b) considerably larger during MIS 4 than during MIS 2, which is not supported by geological evidence (Barrett et al., 2017; Haldimann et al., 2017; Ivy-Ochs et al., 2008; Preusser, 2004; van Husen and Reitner, 2011). Gravel deposits from the Rhine Glacier indicate an early last glacial cycle foreland glaciation, but the extent reached is less than that in MIS 2 (Keller and Krayss, 2010). Dropstones in lake sediments indicate a late MIS 4 advance restricted to the upper Inn Valley (Barrett et al., 2017). For the Linth Glacier, no evidence for a pre-LGM glacier advance during the last glacial cycle is available (Haldimann et al., 2017).
The EPICA palaeo-temperature forcing, on the other hand, yields a MIS 4 glaciation that is only slightly less expansive than the MIS 2 glaciation (Fig. 3e). The sensitivity of the glaciated area to palaeo-precipitation reductions is mostly limited to the southern terminal lobes of central-Alpine glaciers, where reduced precipitation results in a slightly lesser extent during both MIS 2 and 4 (Fig. 3b and e).
Based on the above considerations on timing of the LGM during MIS 2, and modelled ice extent during MIS 4, we select EPICA as our optimal palaeo-temperature record for a more detailed and higher-resolution comparison of modelled glacier dynamics to available geological evidence (Sect. 4). As a conservative approach in regard to the rapid ice volume fluctuations, we choose to include palaeo-precipitation corrections in the following higher-resolution run.
In this section, we compare the model output to geological evidence from the last glacial cycle, in terms of Last Glacial Maximum extent (Sect. 4.1), ice flow patterns (Sect. 4.2), timing of the Last Glacial Maximum (Sect. 4.3), ice thickness (Sect. 4.4), and glacial cycle dynamics (Sect. 4.5).
This simulation is forced by the optimal EPICA palaeo-temperature record (Sect. 3.1) and includes palaeo-precipitation reductions (Sect. 3.2). It uses a horizontal resolution of 1 km. The vertical grid consists of 61 temperature layers in the bedrock and up to 251 enthalpy layers in the ice, corresponding to vertical resolutions of 50 and 20 m, respectively.
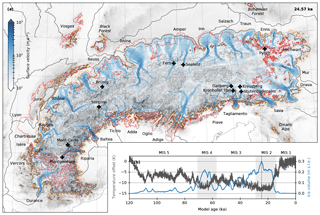
Figure 4(a) Modelled bedrock topography (grey), ice surface topography (200 m contours), and ice surface velocity (blue) in the Alps 24.57 ka before present, corresponding to the modelled maximum ice cover. The modelled LGM ice extent (dashed orange line), geomorphological reconstruction (Ehlers et al., 2011), and some major transfluences across mountain passes (crosses) are shown. (b) Temperature offset time series from the EPICA ice core used as palaeo-climate forcing for the ice flow model (Jouzel et al., 2007), and modelled total ice volume through the last glacial cycle (120–0 ka), expressed in metres of sea level equivalent (m s.l.e., blue curve). Shaded grey areas indicate the timing for marine oxygen isotope stage (MIS) 2 and MIS 4 according to a global compilation of benthic δ18O records (Lisiecki and Raymo, 2005). The black vertical line indicates the modelled age of maximum ice cover at 24.57 ka.
4.1 Last Glacial Maximum ice extent
The LGM extent of Alpine glaciers has been mapped with varying level of detail across the Western (Bini et al., 2009; Buoncristiani and Campy, 2011; Coutterand, 2010; Hantke, 2011; Jäckli, 1962), and Eastern Alps (BGR, 2007; Bavec and Verbič, 2011; Castiglioni, 1940; Penck and Brückner, 1909; van Husen, 1987, 2011). Some of these maps have been compiled into a reconstruction, covering the entire Alps (Ehlers et al., 2011), and reproduced here (Fig. 4, red line) for comparison against model results.
The modelled total ice volume reaches a maximum of 123×103 km3, or 300 mm of sea-level equivalent, at 24.56 ka (Fig. 4b). A maximum glacierized area of 163×103 km2 is attained shortly afterwards at 24.57 ka (Fig. 4a). Although the modelled timing of the LGM varies across the mountain range (Sect. 4.3), at 24.57 ka nearly all outlet glaciers extend to within a few kilometres from their modelled maximum stage (Fig. 4a, dashed orange line).
The palaeo-climate forcing was adapted (Sect. 3.1) to model the maximum configuration of the Rhine Glacier in broad agreement with the geological reconstruction of the LGM extent (Fig. 4a, solid red line), yet discrepancies remain elsewhere. As already outlined for low resolution runs (Sect. 3.4), the extent of glaciation in the north-western Alps – including the Rhône Glacier complex, the Jura ice cap, and the Lyon Lobe – is underestimated in the model results (Bini et al., 2009; Coutterand, 2010). On the other hand, the model yields excessive ice cover in the Eastern Alps, where the Mur, Drava, and Sava glaciers are modelled to extend tens of kilometres beyond the mapped ice limits (Bavec and Verbič, 2011; van Husen, 1987). As previously discussed, these discrepancies might indicate that the LGM climate was characterized by an east–west gradient in temperature (Heyman et al., 2013) or precipitation (Wu et al., 2007), anomalies relative to present, or an east–west gradient in variables that are not accounted for by the PDD model.
On the other hand, while atmospheric circulation models (Ludwig et al., 2016; Strandberg et al., 2011) and palaeo-climate proxies (Luetscher et al., 2015) both support differential precipitation changes north and south of the Alps, our model results show no obvious north–south bias as compared to the mapped LGM margins (Fig. 4a) despite the homogeneous temperature and precipitation anomalies applied relative to present. Although this may appear as a contradiction with previous, constant-climate modelling results (Becker et al., 2016; Jouvet et al., 2017a), it follows from introducing a time-dependent palaeo-temperature forcing. Without introducing differential precipitation change north and south of the Alps, constant climate forcing systematically resulted in extraneous (Becker et al., 2016) and premature (Becker et al., 2016) glaciation on the north slope of the Alps. Using time-dependent palaeo-temperature forcing, progressive atmospheric cooling over several thousand years allows for warmer temperatures – closer to the thermodynamic equilibrium – within the ice and the bedrock. This results in thinner glaciers and limits overshoot of the equilibrium state (discussed further in Sect. 4.3).
On a more regional level, the maximum extent of the Adda, Oglio, Adige, and Piave glaciers in the central southern Alps is modelled several kilometres within the mapped LGM moraines (Fig. 4a). This appears to result from the palaeo-precipitation reduction used to force the model (Fig. 3b), which is likely unrealistic in at least this part of the model domain. On the other hand, the Durance Glacier in the south-western Alps is modelled to extend several kilometres beyond the mapped limit (Fig. 4a), indicating that the LGM temperature depression was likely dampened by the Mediterranean climate in this part of the model domain. However, geochronological data from the south-western Alps are sparse, and the LGM extent compilation (Ehlers et al., 2011) is inconsistent with more recent regional reconstructions (Federici et al., 2017).
The model reproduces peripheral ice caps where documented by geological evidence on the Vercors, Chartreuse, and Bauge Prealpine reliefs, the Jura Mountains, the Vosges Mountains, the Black Forest, the Bohemian Forest and the Dinaric Alps (Fig. 4a). An independent ice cap also covers the Hochwart massif during most of the simulation, yet it is engulfed by Alpine glaciers during the LGM to become a peripheral ice dome (van Husen, 2011). The LGM extent of peripheral ice caps is underestimated in the Vosges and Jura mountains, but it is overestimated for the more meridional Vercors Massif (Coutterand, 2010). Thus, there exists a regional conformity between the model–data discrepancies obtained for the main Alpine ice sheet and those obtained for peripheral ice caps, including too extensive modelled ice cover to the east and extreme south-west, and too restrictive modelled ice cover to the north-west. Because peripheral ice caps have very different glacier dynamics than the main ice sheet, this conformity most likely indicates a climatic cause, rather than an ice dynamics cause, for these discrepancies.
4.2 Ice flow patterns
The LGM Alpine ice flow pattern is traditionally described as that of a network of interconnected valley glaciers, which are primarily controlled by subglacial topography. However, geomorphology shows that ice was thick enough to flow across high mountain passes throughout the mountain range (Coutterand, 2010; Jäckli, 1962; Kelly et al., 2004; Onde, 1938; Penck and Brückner, 1909; van Husen, 1985, 2011), and even perhaps to form self-sustained ice domes (Bini et al., 2009; Florineth, 1998; Florineth and Schlüchter, 1998; Kelly et al., 2004).
The modelled flow pattern at 24.57 ka is complex (Fig. 4a, blue colour mapping). Ice velocities of several hundred metres per year – characteristic of basal sliding – generally occur along the main river valleys, while ice domes and ice divides are predominantly located over major relief areas, where ice moves only by a few metres per year, characteristic of internal deformation without basal sliding (Fig. 4a). Nevertheless, the model results depict exceptions to this general pattern as occasional ice flow across the modern water divides, i.e. transfluences.
In the Western Alps, major transfluences occur for instance across Col de Montgenèvre, Col du Mont-Cenis, Simplon Pass and Brünig Pass (Fig. 4a). Although a transfluence across Col de Montgenèvre was previously questioned (Cossart et al., 2012), evidence for southerly ice flow across Col du Mont-Cenis has been recognized (Coutterand, 2010; Onde, 1938). Similarly, transfluences have been previously identified from the geomorphology across Simplon Pass (Kelly et al., 2004) and from the distribution of glacial erratics across Brünig Pass (Jäckli, 1962). On the other hand, the simplified climate forcing used in this simulation could not reproduce the transport of glacial erratics from southern Valais to observed deposition sites in the Solothurn region (Jouvet et al., 2017a).
In the Eastern Alps, major transfluences are modelled to have occurred for instance across Fern Pass, the Seefeld Saddle, the Gailberg Saddle, the Kreuzberg Saddle, Kronhof Pass, Studenbodenalm, and Pyhrn Pass (Fig. 4a). Transfluences across Fern Pass and the Seefeld Saddle are known from the geomorphology (Penck and Brückner, 1909; van Husen, 2011). It is also known that ice flowed across the Gailberg and Kreuzberg saddles (van Husen, 1985) as well as Pyhrn Pass (van Husen, 2011). On the other hand, no transfluence has previously been documented over the Kronhof Pass, Studenbodenalm or elsewhere over the Carnic Alps. The Tagliamento catchment is usually assumed to not have received transfluences from the Drava catchment (Monegato et al., 2007), but this would not be incompatible with reconstructed ice surface elevations in this area (van Husen, 1987).
Except for too extensive ice cover in the easternmost part of the model domain (Sect. 4.1), there is generally a good agreement between transfluences observed in the geomorphology and the model results. Both depict the LGM Alpine ice flow pattern as an intermediate between that of a topography-controlled ice field, and that of a self-sustained ice cap.
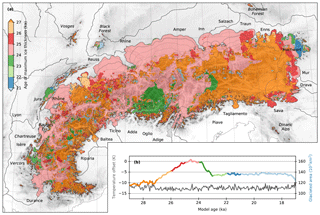
Figure 5(a) Timing of the LGM given by the modelled age of maximum ice thickness throughout the entire simulation (colour mapping) and corresponding, ice surface elevation (200 m contours). (b) Temperature offset time series from the EPICA ice core used as palaeo-climate forcing for the ice flow model (black curve), and modelled glacierized area during the LGM (coloured curve). The LGM is here modelled as a time-transgressive event. In much of the mountain area, maximum thickness is reached before 27 ka.
4.3 Timing of the Last Glacial Maximum
The timing of the LGM has been documented by radiocarbon and cosmogenic isotope dating techniques at multiple locations around the Alps (cf. reviews by Ivy-Ochs, 2015, and Wirsig et al., 2016, and the more recent publications by Federici et al., 2017, Monegato et al., 2017, Gild et al., 2018, and Ivy-Ochs et al., 2018). These data indicate that Alpine glaciers reached their maximum extent between 26 and 20 ka (calibrated 14C and 10Be ages), but also that terminal lobes stayed in the foreland until 22 ka to 17 ka, when they experienced a rapid retreat synchronously with the lowering of the ice surface in the mountains (Ivy-Ochs, 2015; Wirsig et al., 2016; Monegato et al., 2017).
In our simulation, the maximum areal cover is reached at 24.57 ka (Fig. 4a), yet individual glacier lobes reach their maximum extent at different ages (Fig. 5). For instance, the Dora Riparia, Dora Baltea, and Tagliamento glaciers reach an early maximum before 27 ka; the Durance, Rhône, Inn, Enns, Ticino, and Adige glaciers reach their maximum thickness in phase with the overall Alpine areal maximum around 25 ka; while the Isère, Adda and Oglio glaciers reach a late maximum after 24 ka (Fig. 5). Remarkably, peripheral ice caps on the Vercors, Jura Mountains, Black Forest and Hochschwab reach their maximum extent even later and locally after 21 ka (Fig. 5).
These differences in timing of the LGM occur in the model results despite the homogeneous temperature and precipitation anomalies supplied as palaeo-climate forcing. The LGM timing differences modelled here are thus not related to climate, but are inherent to modelled glacier dynamics. They result from differences in the subglacial topography, in particular catchment sizes and hypsometry, of the different outlet glaciers.
For large Alpine glaciers flowing in deep valleys, such as the Rhône, Rhine and Adige glaciers, several thousand model years are needed to attain a thermodynamical equilibrium between cold-ice advection from the high accumulation areas, upward diffusion of geothermal heat, and heat release from strong basal shear strain. Temperature evolution is, in part, limited by the slow warming of the subglacial bedrock, that has been previously cooled downed by subfreezing air temperature before glacier advance. For larger glaciers, this thermodynamical equilibrium is typically not yet attained by around 25 ka. Several Alpine lobes surge and overshoot their balanced extent before thinning and receding towards the mountains as they warm towards thermodynamical equilibrium (supplementary animation in Seguinot, 2018c). In contrast, peripheral ice caps with basal topography restricted to high elevations experience very low shear strain and virtually no basal sliding. They advance regularly on a frozen bed during the entire cold period, resulting in a late maximum stage (Fig. 5).
Our results indicate that even for a relatively small ice sheet like that found in the Alps, the LGM glacier extent corresponds to a transient stage, while millennial-scale spatial differences in its timing can result not only from climate variability but also from complex glacier dynamics. Heterogeneous climatic anomalies, such as temperature or precipitation anomaly gradients, which are not included in our model set-up, could perhaps induce further spatial differences in the timing of the LGM Alpine ice sheet, which may counterbalance or enhance those modelled here.
4.4 Ice thickness and trimlines
Following the general assumption that trimlines, which mark the transition between the steep frost-shattered ridges and the more gentle glacially sculpted valley troughs, represent the maximum elevation of the LGM ice surface, the maximum ice thickness in the Alps has been reconstructed in several areas (Bini et al., 2009; Cossart et al., 2012; Coutterand, 2010; Florineth, 1998; Florineth and Schlüchter, 1998; Kelly et al., 2004; van Husen, 1987). However, this assumption is challenged by geomorphological and cosmogenic nuclide dating evidence from Scandinavia (Kleman, 1994; Kleman and Borgström, 1994), the British Isles (Ballantyne and Stone, 2015; Fabel et al., 2012), and North America (Kleman et al., 2010), that pre-glacial landscapes located well above the trimlines have been glaciated and preserved under cold-based ice, sometimes for several glacial cycles (Stroeven et al., 2002). Thus, the trimline could also mark the maximum elevation of the transition from temperate to cold-based ice or a late-glacial ice surface elevation (Coutterand, 2010). However, no such evidence has been reported in the Alps. Instead, tree and fire remains record the presence of nunataks in the south-western Alps by 21 ka (Carcaillet and Blarquez, 2017; Carcaillet et al., 2018).
In the upper Rhône Valley, the maximum ice surface elevation reached during MIS 2 in our simulation, corrected for bedrock deformation, is consistently modelled to have occurred several hundred metres above the observed trimline elevations (Fig. 6a and b), with a mean difference of 861 m (and a standard deviation 197 m, Fig. 6b), which is significant in respect to the modelled maximum ice thickness in the Rhône Valley (and the Alps) of 2586 m. This result depends on uncertain basal sliding and ice rheological parameters, the model sensitivity to which was not tested here. However, regional model sensitivity tests show that a modelled surface compatible with the trimline elevations is incompatible with the documented overspilling flow across the Simplon Pass (Becker, 2017; Becker et al., 2017) and LGM palaeo-climate proxy records (Cohen et al., 2018). Unfortunately, validation through the bedrock uplift rate (Kuchar et al., 2012) is not doable in the Alps due its lower values, active tectonics, and uncertainties in geological properties (Mey et al., 2016).
Our model results depict a polythermal LGM Alpine ice cover. Due to sub-freezing temperatures applied in the climate forcing of the model, the entire Alpine ice sheet is capped by an upper layer of cold ice. In major Alpine valleys, such as the upper Rhône Valley, important ice thickness and strain heating contribute to form a layer of temperate ice near the glacier base, allowing basal melt, sliding, and potentially erosion (Fig. 6c, white areas). On the other hand, on the highest mountains, ice cover is too thin and too static to form temperate ice, resulting in cold ice down to the bed and preventing potential erosion (Fig. 6c, hatched areas).
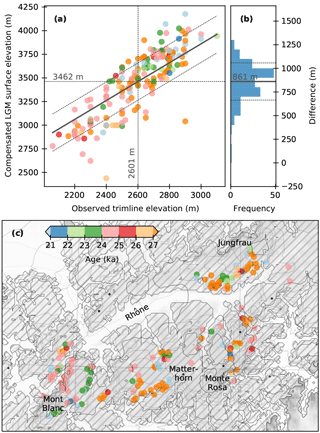
Figure 6(a) Comparison of modelled ice surface elevation at the LGM (time-transgressive, corresponding to maximum ice thickness, Fig. 5), compensated for bedrock deformation, against observed trimline elevations for the upper Rhône Glacier (Kelly et al., 2004). Colours show the age of maximum ice thickness (as in Fig. 5). Model variables were bilinearly interpolated to the trimline locations. (b) Histogram of differences between modelled LGM ice surface elevation and trimline elevations (50 m bands). The average difference is 861 m. (c) Observed upper Rhône Valley trimline locations (Kelly et al., 2004), modelled age of maximum ice thickness (colour) and LGM ice surface elevation (200 m contours). Hatches mark the LGM cold-based areas (basal temperature above K below freezing at the age of maximum ice thickness).
In the upper Rhône Valley, observed trimlines are often located near the LGM cold–temperate basal thermal transition or within cold-based areas (Fig. 6c). The remaining discrepancies between the trimline locations and the modelled basal thermal boundary may relate to temporal migrations of the basal thermal boundary, an absence of sliding in warm-based areas, and levelling of small-scale topographic features in the 1 km horizontal grid. They call for more detailed comparisons spanning the entire Alpine range and specific sensitivity studies to relevant basal sliding and ice rheological parameters, as well as to the uncertain subglacial topography. However, the presence of an upper layer of cold ice during the LGM, already found at high altitudes in the much warmer climate of today (Bohleber et al., 2018; Suter et al., 2001), is inevitable (Blatter and Haeberli, 1984; Cohen et al., 2018; Haeberli and Schlüchter, 1987). The bedrock thermal model yields significant volumes of frozen ground periglacially north of the Alps and subglacially under the highest mountains, which is also in agreement with previous studies (Cohen et al., 2018; Haeberli et al., 1984; Lindgren et al., 2016).
In this context, our results challenge the assumption that Alpine trimlines mark the maximum upper ice surface elevation of the LGM ice cover and call for a more accurate estimation of the thickness of the upper layer of cold ice in the Alps.
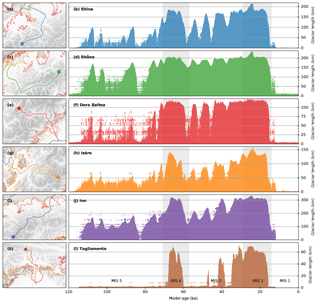
Figure 7(a, c, e, g, i, k) Profile lines roughly following valley centerlines for the Rhine, Rhône, Dora Baltea and Isère, Inn and Tagliamento glaciers. (b, d, f, h, j, l) Evolution of modelled glacier extent in time, bilinearly interpolated along the corresponding profiles, showing numerous cycles of advance and retreat over the last glacial cycle modulated by subglacial topography and catchment geometry. Shaded grey areas indicate the timing for MIS 2 and MIS 4 (Lisiecki and Raymo, 2005). Isolated patches indicate episodic advances from tributary glaciers.
4.5 Glacial cycle dynamics
Glacial history of the Alps prior to the LGM remains poorly constrained. Although the four glaciations model (Penck and Brückner, 1909) has long been used, it is now known that glaciers advanced onto the foreland at least fifteen times since the beginning of the Quaternary at 2.58 Ma (Preusser et al., 2011; Schlüchter, 1991). Sparse geological data indicate that the last glacial cycle may have comprised two or even three periods of glacier growth and decay (Ivy-Ochs et al., 2008; Preusser, 2004). Luminescence dating from two sites in the central northern foreland indicate an early last glacial advance of Alpine glaciers onto the near foreland from around 107±9 to 101±5 ka (Preusser and Schlüchter, 2004; Preusser et al., 2003). Evidence for a MIS 4 glaciation is equally sparse (Barrett et al., 2017; Haldimann et al., 2017; Keller and Krayss, 2010) and its timing remains uncertain (Link and Preusser, 2006; Preusser et al., 2007). During MIS 3, major Eastern Alpine valleys hosted woolly mammoths (Spötl et al., 2018) and open vegetation (Barrett et al., 2018), indicating more restricted glaciation.
As previously mentioned (Sect. 3.3), independent of the palaeo-temperature (GRIP, EPICA, or MD01-2444) and palaeo-precipitation (with or without corrections) applied, all simulations presented here result in a high temporal variability in the total modelled ice volume (Fig. 2). Using the optimal EPICA palaeo-temperature record with least variability (Sect. 3.1) and conservatively including palaeo-precipitation reductions (Sect. 3.2), the 1 km resolution simulation also results in strong total ice volume variability throughout the last glacial cycle (Fig. 4b). Two major glaciations occur during MIS 4 and 2 (Fig. 4b). However, several minor glaciations occur during MIS 5 and 3, as well as a minor late-glacial re-advance at the onset of MIS 1 (Fig. 4b). These episodes are the result of synchronous advances of several Alpine glaciers well into the major valleys and sometimes even onto the foreland (Fig. 7; supplementary animation).
For instance the Rhine Glacier (Fig. 7a) extends beyond the outermost limestone reliefs six times during the simulation, and sometimes retreats almost completely between two advances (Fig. 7b). The Rhône Glacier, fed by several high-altitude accumulation areas, advances eight times onto modern Lake Geneva (Fig. 7c and d). The Dora Baltea Glacier, characterized by a very steep catchment, and multiple tributaries, shows even a higher variability and reaches close to its maximum position six times throughout the simulation (Fig. 7e and f). The Isère (Fig. 7g and h) and Inn (Fig. 7i and j) glaciers, with their complex system of confluences and diffluences, need longer time to build up and reach the foreland only two or three times (Fig. 7g–j). Finally, the Tagliamento Glacier, distant from the major ice-dispersal centres of the inner Alps, is absent for most of the modelled glacial cycle (Fig. 7k and l)
Despite the low temperature variability of the palaeo-climate forcing and reduced precipitation dampening glacier response, our simulation depicts the Alpine ice complex as highly dynamic, with many more than two or three (Ivy-Ochs et al., 2008; Preusser, 2004) glaciations and regional glacier dynamics controlled by spatial variations in catchment size and hypsometry. Importantly, Dansgaard–Oeschger events, recorded in Europe (Luetscher et al., 2015; Spötl and Mangini, 2002; Wohlfarth et al., 2008) but absent from the EPICA palaeo-temperature forcing, may have induced an even more dynamic glacier response than that modelled here.
In this study the numerical ice sheet model PISM (Sect. 2) has been applied to ice dynamics of the last glacial cycle in the Alps. Using three different palaeo-temperature forcing records (GRIP, EPICA, and MD01-2444; Sect. 3.1), scaled to reproduce the Rhine Glacier piedmont lobe in agreement with the mapped LGM ice margin, and two different palaeo-precipitation parametrizations (with and without ca. −68 precipitation reductions; Sect. 3.2), we find that only the EPICA palaeo-temperature record yields model results in agreement with geological findings, in the following sense:
-
The EPICA palaeo-temperature forcing yields maximum ice volume at 25.2/24.6 ka (without/with palaeo-precipitation reduction), followed by a standstill of major piedmont lobes in the forelands until 17.3 ka, both compatible with much of the dating results, whereas the GRIP forcing results in early deglaciation of the foreland complete by 21.4 ka, and the MD01-2444 forcing results in a late LGM glaciation peaking at 16.5/15.7 ka (Sect. 3.3).
-
The EPICA palaeo-temperature forcing yields cumulative ice extent compatible with geological evidence during MIS 4 and 2, whereas both GRIP and MD01-2444 records result in MIS 4 glaciation well beyond the mapped LGM ice limits (Sect. 3.4).
This interesting result may be coincidental as there is no direct link between European and Antarctic climate. This highlights the need for more quantitative reconstructions of European palaeoclimate.
We then use this optimal palaeo-temperature forcing, and as a conservative approach, palaeo-precipitation reductions, to force a 1 km resolution simulation of the last glacial cycle in the Alps. A more detailed analysis of its output led us to the following conclusions.
-
Ice cover is generally underestimated in the north-western Alps and overestimated in the eastern and south-western Alps, indicating that east–west gradients in temperature or precipitation change, absent from our model forcing, probably controlled the LGM extent of ice cover in the Alps. The observed asymmetric extent of ice north and south of the Alps can be explained by the modelled transient nature of the LGM extent without involving north–south gradients in temperature and precipitation change (Sect. 4.1).
-
The LGM ice flow pattern in the Alps was largely controlled by subglacial topography, but transfluences across several mountain passes may have occurred (Sect. 4.2).
-
The LGM (maximum) extent was a transient stage in which glaciers were out of balance with the contemporary climate. Its timing potentially varied across the range due to inherent glacier dynamics (Sect. 4.3).
-
Ice thickness during the LGM is modelled to be much larger than in reconstructions. On average, modelled surface elevation is 861 m above the Rhône Glacier trimlines, which may instead indicate an englacial thermal boundary (Sect. 4.4).
-
Alpine glaciers were very dynamic. They quickly responded to climate fluctuations and some potentially advanced many times over the foreland during the last glacial cycle (Sect. 4.5).
However, these results are limited by uncertainties in glacier physics. The till deformation model used here does not hold for sliding over bedrock surfaces. On the other hand, the constant friction angle used is representative of wet till, but weaker basal conditions may have applied over saturated lake sediments where they occurred. In the absence of ice deformation measurements, a constant rheology was used for temperature ice containing more than 1 % of liquid water.
More importantly, these results are limited by the simplicity of the surface mass balance parameters and climate forcing used. In particular, additional palaeo-climate variability over the European Alps may have caused more glaciations than modelled here. Shifts in the North Atlantic storm track and polar front may have caused varied patterns of glaciations through different cold phases. Using more specifically targeted sensitivity runs, and a more realistic climate forcing based on regional circulation model output, or including the effect of long-term changes in incoming solar radiation, future modelling studies will certainly be able to quantify uncertainties associated with some of the above limitations. Nevertheless, we hope that these conclusions will also serve as a basis for future studies of glacial geology in the Alps and call for a more systematic aggregation and homogenization of glacial geological data to form a basis for model validation across the entire Alpine range.
PISM is available as open-source software at http://pism-docs.org. Aggregated variables used in the figures (https://doi.org/10.5281/zenodo.1423160, 35 MB) and a subset of continuous model variables (https://doi.org/10.5281/zenodo.1423176, 1 GB) have been made available. Original model output (1.8 TB) will be stored by the first author for a limited time. The supplementary animation can be found at https://doi.org/10.5446/35164.
JS designed the study, ran the simulations, and wrote most of the manuscript. All authors contributed in interpreting the results and improving the text. MH provided modern ice thickness data. The idea for this study stems in part from an excursion organized by FP in the central Alps in 2012.
The authors declare that they have no conflict of interest.
We are very thankful to Constantine Khroulev, Ed Bueler, and Andy Aschwanden
for providing constant help and development with PISM, in particular with
recent issues with the computation of ice temperature (Github issue no. 371)
and with the computation of bedrock deformation (Github issues no. 370 and
377). We are equally thankful to three anonymous reviewers, Giovanni
Monagato, and the editor Andreas Vieli for their meticulous readings and
constructive inputs during peer-review. We thank Marc Luetscher for an
insightful discussion of preliminary results during the EGU General
Assembly 2017. The experimental design and article layout used here are based
on previous work which received much guidance from Irina Rogozhina and
Arjen P. Stroeven. The current work was supported by the Swiss National
Science Foundation grants no. 200020-169558 and 200021-153179/1 to
Martin Funk. Computer resources were provided by the Swiss National
Supercomputing Centre (CSCS) allocations no. s573 and sm13 to
Julien Seguinot.
Edited by: Andreas Vieli
Reviewed by: three anonymous referees
Agassiz, L.: Etudes sur les glaciers, Jent et Gassmann, Soleure, 1840. a
Aschwanden, A., Bueler, E., Khroulev, C., and Blatter, H.: An enthalpy formulation for glaciers and ice sheets, J. Glaciol., 58, 441–457, https://doi.org/10.3189/2012JoG11J088, 2012. a, b, c, d, e, f, g
Aschwanden, A., Aðalgeirsdóttir, G., and Khroulev, C.: Hindcasting to measure ice sheet model sensitivity to initial states, The Cryosphere, 7, 1083–1093, https://doi.org/10.5194/tc-7-1083-2013, 2013. a, b, c
Augustin, L., Barbante, C., Barnes, P. R. F., Barnola, J. M., Bigler, M., Castellano, E., Cattani, O., Chappellaz, J., Dahl-Jensen, D., Delmonte, B., Dreyfus, G., Durand, G., Falourd, S., Fischer, H., Flückiger, J., Hansson, M. E., Huybrechts, P., Jugie, G., Johnsen, S. J., Jouzel, J., Kaufmann, P., Kipfstuhl, J., Lambert, F., Lipenkov, V. Y., Littot, G. C., Longinelli, A., Lorrain, R., Maggi, V., Masson-Delmotte, V., Miller, H., Mulvaney, R., Oerlemans, J., Oerter, H., Orombelli, G., Parrenin, F., Peel, D. A., Petit, J.-R., Raynaud, D., Ritz, C., Ruth, U., Schwander, J., Siegenthaler, U., Souchez, R., Stauffer, B., Steffensen, J. P., Stenni, B., Stocker, T. F., Tabacco, I. E., Udisti, R., van de Wal, R. S. W., van den Broeke, M., Weiss, J., Wilhelms, F., Winther, J.-G., Wolff, E. W., and Zucchelli, M.: Eight glacial cycles from an Antarctic ice core, Nature, 429, 623–628, https://doi.org/10.1038/nature02599, 2004. a, b
Ballantyne, C. K. and Stone, J. O.: Trimlines, blockfields and the vertical extent of the last ice sheet in southern Ireland, Boreas, 44, 277–287, https://doi.org/10.1111/bor.12109, 2015. a, b
Barrett, S., Starnberger, R., Tjallingii, R., Brauer, A., and Spötl, C.: The sedimentary history of the inner-alpine Inn Valley, Austria: extending the Baumkirchen type section further back in time with new drilling, J. Quaternary Sci., 32, 63–79, https://doi.org/10.1002/jqs.2924, 2017. a, b, c
Barrett, S. J., Drescher-Schneider, R., Starnberger, R., and Spötl, C.: Evaluation of the regional vegetation and climate in the Eastern Alps (Austria) during MIS 3–4 based on pollen analysis of the classical Baumkirchen paleolake sequence, Quaternary Res., 90, 153–163, https://doi.org/10.1017/qua.2018.26, 2018. a
Barron, E. and Pollard, D.: High-Resolution Climate Simulations of Oxygen Isotope Stage 3 in Europe, Quaternary Res., 58, 296–309, https://doi.org/10.1006/qres.2002.2374, 2002. a
Bavec, M. and Verbič, T.: Chapter 29 – Glacial History of Slovenia, in: Quaternary Glaciations – Extent and Chronology: A Closer Look, edited by: Ehlers, J., Gibbard, P. L., and Hughes, P. D., 15, 385–392, https://doi.org/10.1016/b978-0-444-53447-7.00029-5, 2011. a, b
Becker, P.: Numerische Modellierung der Alpenvergletscherung während des letztglazialen Maximums, PhD thesis, ETH Zürich, Switzerland, https://doi.org/10.3929/ethz-b-000161489, 2017. a
Becker, P., Seguinot, J., Jouvet, G., and Funk, M.: Last Glacial Maximum precipitation pattern in the Alps inferred from glacier modelling, Geogr. Helv., 71, 173–187, https://doi.org/10.5194/gh-71-173-2016, 2016. a, b, c, d
Becker, P., Funk, M., Schlüchter, C., and Hutter, K.: A study of the Würm glaciation focused on the Valais region (Alps), Geogr. Helv., 72, 421–442, https://doi.org/10.5194/gh-72-421-2017, 2017. a, b
BGR: Geologische Übersichtskarte der Bundesrepublik Deutschland , various sheets, Bundesanstalt für Geowissenschaften und Rohstoffe, Hannover, 2007. a
Bini, A., Buoncristiani, J.-F., Couterrand, S., Ellwanger, D., Felber, M., Florineth, D., Graf, H. R., Keller, O., Kelly, M., Schlüchter, C., and Schoeneich, P.: Die Schweiz während des letzteiszeitlichen Maximums (LGM), Bundesamt für Landestopografie swisstopo, 2009. a, b, c, d, e, f
Blatter, H. and Haeberli, W.: Modelling Temperature Distribution in Alpine Glaciers, Ann. Glaciol., 5, 18–22, https://doi.org/10.3189/1984aog5-1-18-22, 1984. a, b
Boch, R., Cheng, H., Spötl, C., Edwards, R. L., Wang, X., and Häuselmann, Ph.: NALPS: a precisely dated European climate record 120–60 ka, Clim. Past, 7, 1247–1259, https://doi.org/10.5194/cp-7-1247-2011, 2011. a
Bohleber, P., Hoffmann, H., Kerch, J., Sold, L., and Fischer, A.: Investigating cold based summit glaciers through direct access to the glacier base: a case study constraining the maximum age of Chli Titlis glacier, Switzerland, The Cryosphere, 12, 401–412, https://doi.org/10.5194/tc-12-401-2018, 2018. a
Bueler, E. and van Pelt, W.: Mass-conserving subglacial hydrology in the Parallel Ice Sheet Model version 0.6, Geosci. Model Dev., 8, 1613–1635, https://doi.org/10.5194/gmd-8-1613-2015, 2015. a, b, c, d
Bueler, E., Lingle, C. S., and Brown, J.: Fast computation of a viscoelastic deformable Earth model for ice-sheet simulations, Ann. Glaciol., 46, 97–105, https://doi.org/10.3189/172756407782871567, 2007. a
Buoncristiani, J.-F. and Campy, M.: Quaternary Glaciations in the French Alps and Jura, in: Quaternary Glaciations – Extent and Chronology: A Closer Look, edited by: Ehlers, J., Gibbard, P. L., and Hughes, P. D., 117–126, https://doi.org/10.1016/b978-0-444-53447-7.00010-6, 2011. a
Calov, R. and Greve, R.: A semi-analytical solution for the positive degree-day model with stochastic temperature variations, J. Glaciol., 51, 173–175, https://doi.org/10.3189/172756505781829601, 2005. a
Carcaillet, C. and Blarquez, O.: Fire ecology of a tree glacial refugium on a nunatak with a view on Alpine glaciers, New Phytol., 216, 1281–1290, https://doi.org/10.1111/nph.14721, 2017. a
Carcaillet, C., Latil, J.-L., Abou, S., Ali, A., Ghaleb, B., Magnin, F., Roiron, P., and Aubert, S.: Keep your feet warm? A cryptic refugium of trees linked to a geothermal spring in an ocean of glaciers, Glob. Change Biol., 24, 2476–2487, https://doi.org/10.1111/gcb.14067, 2018. a
Castiglioni, B.: L'Italia nell'età quaternaria, Carta delle Alpi nel Glaciale, (1 : 200 000 scale), in: Atlante fisico-economico d'Italia, edited by: Dainelli, G., Consociazione Turistica Italiana, Milano, Italy, Table 3, 1940. a, b
Chamberlin, T. C.: Glacial phenomena of North America, in: The great ice age, edited by: Geikie, J., Stanford, London, 3rd edn., 724–775, 1894. a
Cohen, D., Gillet-Chaulet, F., Haeberli, W., Machguth, H., and Fischer, U. H.: Numerical reconstructions of the flow and basal conditions of the Rhine glacier, European Central Alps, at the Last Glacial Maximum, The Cryosphere, 12, 2515–2544, https://doi.org/10.5194/tc-12-2515-2018, 2018. a, b, c, d
Cossart, E., Fort, M., Bourlès, D., Braucher, R., Perrier, R., and Siame, L.: Deglaciation pattern during the Lateglacial/Holocene transition in the southern French Alps. Chronological data and geographical reconstruction from the Clarée Valley (upper Durance catchment, southeastern France), Palaeogeogr. Palaeocl., 315-316, 109–123, https://doi.org/10.1016/j.palaeo.2011.11.017, 2012. a, b
Coutterand, S.: Etude géomorphologique des flux glaciaires dans les Alpes nord-occidentales au Pléistocène récent: du maximum de la dernière glaciation aux premières étapes de la déglaciation, PhD thesis, Université de Savoie, 2010. a, b, c, d, e, f, g, h, i
Cuffey, K. M. and Paterson, W. S. B.: The physics of glaciers, Elsevier, Amsterdam, 2010. a, b, c, d, e, f, g, h, i, j, k, l
Dahl-Jensen, D., Johnsen, S. J., Hammer, C. U., Clausen, H. B., and Jouzel, J.: Past Accumulation rates derived from observed annual layers in the GRIP ice core from Summit, Central Greenland, in: Ice in the Climate System, edited by: Peltier, W. R., NATO ASI Series, 12, 517–532, https://doi.org/10.1007/978-3-642-85016-5_29, 1993. a
Dansgaard, W., Johnsen, S. J., Clausen, H. B., Dahl-Jensen, D., Gundestrup, N. S., Hammer, C. U., Hvidberg, C. S., Steffensen, J. P., Sveinbjörnsdottir, A. E., Jouzel, J., and Bond, G.: Evidence for general instability of past climate from a 250-kyr ice-core record, Nature, 364, 218–220, https://doi.org/10.1038/364218a0, 1993. a, b, c
de Beaulieu, J.-L. and Reille, M.: The last climatic cycle at La Grande Pile (Vosges, France) a new pollen profile, Quaternary Sci. Rev., 11, 431–438, https://doi.org/10.1016/0277-3791(92)90025-4, 1992. a
de Charpentier, J.: Essai sur les glaciers et sur le terrain erratique du bassin du Rhône, Ducloux, Lausanne, https://doi.org/10.3931/e-rara-8464, 1841. a
de Saussure, H.-B.: Voyages dans les Alpes, précédés d'un essai sur l'histoire naturelle des environs de Genève, vol. 1, Fauche-Borel, Neuchâtel, 1779. a
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a, b
Duprat-Oualid, F., Rius, D., Bégeot, C., Magny, M., Millet, L., Wulf, S., and Appelt, O.: Vegetation response to abrupt climate changes in Western Europe from 45 to 14.7 k cal a BP: the Bergsee lacustrine record (Black Forest, Germany), J. Quaternary Sci., 32, 1008–1021, https://doi.org/10.1002/jqs.2972, 2017. a
Duval, P.: The role of the water content on the creep rate of polycrystalline ice, in: Isotopes and impurities in snow and ice, Proceedings of the Grenoble Symposium, August–September 1975, IAHS Publ. no. 118, 29–33, 1977. a
Ehlers, J., Gibbard, P. L., and Hughes, P. D. (Eds.): Supplementary data to Quaternary glaciations – extent and chronology, a closer look, vol. 15 of Dev. Quaternary Sci., Elsevier, Amsterdam, available at: https://booksite.elsevier.com/9780444534477 (last access: 10 February 2016), 2011. a, b, c, d, e, f
Emiliani, C.: Pleistocene Temperatures, J. Geol., 63, 538–578, https://doi.org/10.1086/626295, 1955. a
Fabel, D., Ballantyne, C. K., and Xu, S.: Trimlines, blockfields, mountain-top erratics and the vertical dimensions of the last British-Irish Ice Sheet in NW Scotland, Quaternary Sci. Rev., 55, 91–102, https://doi.org/10.1016/j.quascirev.2012.09.002, 2012. a, b
Federici, P. R., Ribolini, A., and Spagnolo, M.: Glacial history of the Maritime Alps from the Last Glacial Maximum to the Little Ice Age, Geol. Soc. Spec. Publ., 433, 137–159, https://doi.org/10.1144/SP433.9, 2017. a, b
Florineth, D.: Surface geometry of the Last Glacial Maximum (LGM) in the southeastern Swiss Alps (Graubünden) and its paleoclimatological significance, E&G Quaternary Sci. J., 48, 23–37, https://doi.org/10.3285/eg.48.1.03, 1998. a, b
Florineth, D. and Schlüchter, C.: Reconstructing the Last Glacial Maximum (LGM) ice surface geometry and flowlines in the Central Swiss Alps, Eclogae Geol. Helv., 91, 391–407, 1998. a, b
Forbes, J. D.: Illustrations of the Viscous Theory of Glacier Motion. Part III, Philos. T. R. Soc. Lond., 136, 177–210, https://doi.org/10.1098/rstl.1846.0015, 1846. a
Gild, C., Geitner, C., and Sanders, D.: Discovery of a landscape-wide drape of late-glacial aeolian silt in the western Northern Calcareous Alps (Austria): First results and implications, Geology, 301, 39–52, https://doi.org/10.1016/j.geomorph.2017.10.025, 2018. a
Glen, J.: Experiments on the deformation of ice, J. Glaciol., 2, 111–114, 1952. a
Golledge, N. R., Mackintosh, A. N., Anderson, B. M., Buckley, K. M., Doughty, A. M., Barrell, D. J., Denton, G. H., Vandergoes, M. J., Andersen, B. G., and Schaefer, J. M.: Last Glacial Maximum climate in New Zealand inferred from a modelled Southern Alps icefield, Quaternary Res., 46, 30–45, https://doi.org/10.1016/j.quascirev.2012.05.004, 2012. a
Goutorbe, B., Poort, J., Lucazeau, F., and Raillard, S.: Global heat flow trends resolved from multiple geological and geophysical proxies, Geophys. J. Int., 187, 1405–1419, https://doi.org/10.1111/j.1365-246x.2011.05228.x, 2011. a, b
Haeberli, W. and Schlüchter, C.: Geological evidence to constrain modelling of the Late Pleistocene Rhonegletscher (Switzerland), in: The Physical Basis of Ice Sheet Modelling, Proceedings of the Vancouver Symposium, August 1987, IAHS Publ. no. 170, 333–346, 1987. a, b
Haeberli, W., Rellstab, W., and Harrison, W. D.: Geothermal Effects of 18 ka BP Ice Conditions in the Swiss Plateau, Ann. Glaciol., 5, 56–60, https://doi.org/10.3189/1984aog5-1-56-60, 1984. a
Haldimann, P., Graf, H., and Jost, J.: Geological map Bülach (LK 1071), Bundesamt für Landestopografie swisstopo, Wabern, Switzerland, 2017. a, b, c
Hantke, R.: Eiszeitalter : Kalt-/Warmzeit-Zyklen und Eistransport im alpinen und voralpinen Raum, Ott, Bern, 2011. a
Hays, J. D., Imbrie, J., and Shackleton, N. J.: Variations in the Earth's Orbit: Pacemaker of the Ice Ages, Science, 194, 1121–1132, https://doi.org/10.1126/science.194.4270.1121, 1976. a
Heiri, O., Koinig, K. A., Spötl, C., Barrett, S., Brauer, A., Drescher-Schneider, R., Gaar, D., Ivy-Ochs, S., Kerschner, H., Luetscher, M., Moran, A., Nicolussi, K., Preusser, F., Schmidt, R., Schoeneich, P., Schwörer, C., Sprafke, T., Terhorst, B., and Tinner, W.: Palaeoclimate records 60–8 ka in the Austrian and Swiss Alps and their forelands, Quaternary Sci. Rev., 106, 186–205, https://doi.org/10.1016/j.quascirev.2014.05.021, 2014. a, b
Heyman, B. M., Heyman, J., Fickert, T., and Harbor, J. M.: Paleo-climate of the central European uplands during the last glacial maximum based on glacier mass-balance modeling, Quaternary Res., 79, 49–54, https://doi.org/10.1016/j.yqres.2012.09.005, 2013. a, b
Heyman, J., Stroeven, A. P., Harbor, J. M., and Caffee, M. W.: Too young or tooold: Evaluating cosmogenic exposure dating based on an analysis of compiled boulder exposure ages, Earth Planet. Sc. Lett., 302, 71–80, https://doi.org/10.1016/j.epsl.2010.11.040, 2011. a
Hijmans, R. J., Cameron, S. E., Parra, J. L., Jones, P. G., and Jarvis, A.: Very high resolution interpolated climate surfaces for global land areas, Int. J. Climatol., 25, 1965–1978, https://doi.org/10.1002/joc.1276, 2005. a, b, c, d
Hock, R.: Temperature index melt modelling in mountain areas, J. Hydrol., 282, 104–115, https://doi.org/10.1016/S0022-1694(03)00257-9, 2003. a
Huss, M. and Farinotti, D.: Distributed ice thickness and volume of all glaciers around the globe, J. Geophys. Res., 117, F04010, https://doi.org/10.1029/2012JF002523, 2012. a, b
Huybrechts, P.: Report of the third EISMINT workshop on model intercomparison, Tech. rep., Grindelwald, Switzerland, 120 pp., 1998. a, b, c
Huybrechts, P.: Sea-level changes at the LGM from ice-dynamic reconstructions of the Greenland and Antarctic ice sheets during the glacial cycles, Quaternary Sci. Rev., 21, 203–231, https://doi.org/10.1016/s0277-3791(01)00082-8, 2002. a, b
Isotta, F. A., Frei, C., Weilguni, V., Tadić, M. P., Lassègues, P., Rudolf, B., Pavan, V., Cacciamani, C., Antolini, G., Ratto, S. M., Munari, M., Micheletti, S., Bonati, V., Lussana, C., Ronchi, C., Panettieri, E., Marigo, G., and Vertačnik, G.: The climate of daily precipitation in the Alps: development and analysis of a high-resolution grid dataset from pan-Alpine rain-gauge data, Int. J. Climatol., 34, 1657–1675, https://doi.org/10.1002/joc.3794, 2013. a
Ivy-Ochs, S.: Glacier variations in the European Alps at the end of the last glaciation, Cuadernos de Investigación Geográfica, 41, 295–315, https://doi.org/10.18172/cig.2750, 2015. a, b, c, d
Ivy-Ochs, S., Kerschner, H., Kubik, P. W., and Schlüchter, C.: Glacier response in the European Alps to Heinrich Event 1 cooling: the Gschnitz stadial, J. Quaternary Sci., 21, 115–130, https://doi.org/10.1002/jqs.955, 2006. a
Ivy-Ochs, S., Kerschner, H., Reuther, A., Preusser, F., Heine, K., Maisch, M., Kubik, P. W., and Schlüchter, C.: Chronology of the last glacial cycle in the European Alps, J. Quaternary Sci., 23, 559–573, https://doi.org/10.1002/jqs.1202, 2008. a, b, c, d, e, f, g, h, i, j
Ivy-Ochs, S., Kerschner, H., Maisch, M., Christl, M., Kubik, P. W., and Schlüchter, C.: Latest Pleistocene and Holocene glacier variations in the European Alps, Quaternary Sci. Rev., 28, 2137–2149, https://doi.org/10.1016/j.quascirev.2009.03.009, 2009. a
Ivy-Ochs, S., Lucchesi, S., Baggio, P., Fioraso, G., Gianotti, F., Monegato, G., Graf, A. A., Akçar, N., Christl, M., Carraro, F., Forno, M. G., and Schlüchter, C.: New geomorphological and chronological constraints for glacial deposits in the Rivoli-Avigliana end-moraine system and the lower Susa Valley (Western Alps, NW Italy), J. Quaternary Sci., 33, 550–562, https://doi.org/10.1002/jqs.3034, 2018. a
Jäckli, H.: Die Vergletscherung der Schweiz im Würm maximum, Eclogae Geol. Helv., 55, 12 pp., https://doi.org/10.5169/seals-162924, 1962. a, b, c
Jarvis, A., Reuter, H., Nelson, A., and Guevara, E.: Hole-filled SRTM for the globe Version 4, available from the CGIAR-CSI SRTM 90 m Database, available at: http://srtm.csi.cgiar.org (last access: 28 April 2017), 2008. a, b
Johnsen, S. J., Dahl-Jensen, D., Dansgaard, W., and Gundestrup, N.: Greenland palaeotemperatures derived from GRIP bore hole temperature and ice core isotope profiles, Tellus B, 47, 624–629, https://doi.org/10.1034/j.1600-0889.47.issue5.9.x, 1995. a
Jouvet, G., Seguinot, J., Ivy-Ochs, S., and Funk, M.: Modelling the diversion of erratic boulders by the Valais Glacier during the last glacial maximum, J. Glaciol., 63, 487–498, https://doi.org/10.1017/jog.2017.7, 2017. a, b, c
Jouzel, J., Masson-Delmotte, V., Cattani, O., Dreyfus, G., Falourd, S., Hoffmann, G., Minster, B., Nouet, J., Barnola, J. M., Chappellaz, J., Fischer, H., Gallet, J. C., Johnsen, S., Leuenberger, M., Loulergue, L., Luethi, D., Oerter, H., Parrenin, F., Raisbeck, G., Raynaud, D., Schilt, A., Schwander, J., Selmo, E., Souchez, R., Spahni, R., Stauffer, B., Steffensen, J. P., Stenni, B., Stocker, T. F., Tison, J. L., Werner, M., and Wolff, E. W.: Orbital and Millennial Antarctic Climate Variability over the Past 800,000 Years, Science, 317, 793–796, https://doi.org/10.1126/science.1141038, 2007. a, b, c
Keller, O. and Krayss, E.: Mittel- und spätpleistozäne Stratigraphie und Morphogenese in Schlüsselregionen der Nordschweiz, E&G Quaternary Sci. J., 59, 88–119, https://doi.org/10.3285/eg.59.1-2.08, 2011. a, b
Kelly, M. A., Buoncristiani, J.-F., and Schlüchter, C.: A reconstruction of the last glacial maximum (LGM) ice surface geometry in the western Swiss Alps and contiguous Alpine regions in Italy and France, Eclogae Geol. Helv., 97, 57–75, 2004. a, b, c, d, e, f, g
Kjellström, E., Brandefelt, J., Näslund, J.-O., Smith, B., Strandberg, G., Voelker, A. H. L., and Wohlfarth, B.: Simulated climate conditions in Europe during the Marine Isotope Stage 3 stadial, Boreas, 39, 436–456, https://doi.org/10.1111/j.1502-3885.2010.00143.x, 2010. a
Kleiner, T., Rückamp, M., Bondzio, J. H., and Humbert, A.: Enthalpy benchmark experiments for numerical ice sheet models, The Cryosphere, 9, 217–228, https://doi.org/10.5194/tc-9-217-2015, 2015. a
Kleman, J.: Preservation of landforms under ice sheets and ice caps, Geomorphology, 9, 19–32, https://doi.org/10.1016/0169-555x(94)90028-0, 1994. a, b, c
Kleman, J. and Borgström, I.: Glacial land forms indicative of a partly frozen bed, J. Glaciol., 40, 255–264, https://doi.org/10.1017/S0022143000007346, 1994. a
Kleman, J., Hättestrand, C., Stroeven, A. P., Jansson, K. N., De Angelis, H., and Borgström, I.: Reconstruction of Palaeo-Ice Sheets – Inversion of their Glacial Geomorphological Record, in: Glacier Science and Environmental Change, edited by: Knight, P. G., Blackwell, Malden, MA, 192–198, https://doi.org/10.1002/9780470750636.ch38, 2006. a
Kleman, J., Jansson, K., De Angelis, H., Stroeven, A., Hättestrand, C., Alm, G., and Glasser, N.: North American ice sheet build-up during the last glacial cycle, 115–21 kyr, Quaternary Sci. Rev., 29, 2036–2051, https://doi.org/10.1016/j.quascirev.2010.04.021, 2010. a, b, c
Kuchar, J., Milne, G., Hubbard, A., Patton, H., Bradley, S., Shennan, I., and Edwards, R.: Evaluation of a numerical model of the British-Irish ice sheet using relative sea-level data: implications for the interpretation of trimline observations, J. Quaternary Sci., 27, 597–605, https://doi.org/10.1002/jqs.2552, 2012. a
Lindgren, A., Hugelius, G., Kuhry, P., Christensen, T. R., and Vandenberghe, J.: GIS-based Maps and Area Estimates of Northern Hemisphere Permafrost Extent during the Last Glacial Maximum, Palaeogeogr. Palaeocl., 27, 6–16, https://doi.org/10.1002/ppp.1851, 2016. a
Lingle, C. S. and Clark, J. A.: A numerical model of interactions between a marine ice sheet and the solid Earth: application to a West Antarctic ice stream, J. Geophys. Res., 90, 1100–1114, https://doi.org/10.1029/JC090iC01p01100, 1985. a
Link, A. and Preusser, F.: Hinweise auf eine Vergletscherung des Kemptener Beckens während des Mittelwürms, Eiszeitalter und Gegenwart, 55, 65–88, https://doi.org/10.3285/eg.55.1, 2006. a
Lisiecki, L. E. and Raymo, M. E.: A Pliocene-Pleistocene stack of 57 globally distributed benthic δ18O records, Paleoceanography, 20, PA1003, https://doi.org/10.1029/2004pa001071, 2005. a, b, c, d
Lliboutry, L. A. and Duval, P.: Various isotropic and anisotropic ices found in glaciers and polar ice caps and their corresponding rheologies, Ann. Geophys., 3, 207–224, 1985. a, b
Love, A. E. H.: A treatise on the mathematical theory of elasticity, 2nd edn., Cambridge University Press, Cambridge, UK, 1906. a
Ludwig, P., Schaffernicht, E. J., Shao, Y., and Pinto, J. G.: Regional atmospheric circulation over Europe during the Last Glacial Maximum and its links to precipitation, J. Geophys. Res.-Atmos., 121, 2130–2145, https://doi.org/10.1002/2015jd024444, 2016. a, b
Luetscher, M., Boch, R., Sodemann, H., Spötl, C., Cheng, H., Edwards, R. L., Frisia, S., Hof, F., and Müller, W.: North Atlantic storm track changes during the Last Glacial Maximum recorded by Alpine speleothems, Nature Communications, 6, 6344, https://doi.org/10.1038/ncomms7344, 2015. a, b, c, d
Lüthi, M., Funk, M., Iken, A., Gogineni, S., and Truffer, M.: Mechanisms of fast flow in Jakobshavns Isbræ, Greenland; Part III: measurements of ice deformation, temperature and cross-borehole conductivity in boreholes to the bedrock, J. Glaciol., 48, 369–385, https://doi.org/10.3189/172756502781831322, 2002. a
Martrat, B., Grimalt, J. O., Shackleton, N. J., de Abreu, L., Hutterli, M. A., and Stocker, T. F.: Four climate cycles of recurring deep and surface water destabilizations on the Iberian margin, Science, 317, 502–507, https://doi.org/10.1126/science.1139994, 2007. a, b
Mesinger, F., DiMego, G., Kalnay, E., Mitchell, K., Shafran, P. C., Ebisuzaki, W., Jović, D., Woollen, J., Rogers, E., Berbery, E. H., Ek, M. B., Fan, Y., Grumbine, R., Higgins, W., Li, H., Lin, Y., Manikin, G., Parrish, D., and Shi, W.: North American regional reanalysis, B. Am. Meteorol. Soc., 87, 343–360, https://doi.org/10.1175/BAMS-87-3-343, 2006. a
Mey, J., Scherler, D., Wickert, A. D., Egholm, D. L., Tesauro, M., Schildgen, T. F., and Strecker, M. R.: Glacial isostatic uplift of the European Alps, Nature Communications, 7, 13382, https://doi.org/10.1038/ncomms13382, 2016. a, b, c, d, e, f, g, h
Monegato, G., Ravazzi, C., Donegana, M., Pini, R., Calderoni, G., and Wick, L.: Evidence of a two-fold glacial advance during the last glacial maximum in the Tagliamento end moraine system (eastern Alps), Quaternary Res., 68, 284–302, https://doi.org/10.1016/j.yqres.2007.07.002, 2007. a
Monegato, G., Scardia, G., Hajdas, I., Rizzini, F., and Piccin, A.: The Alpine LGM in the boreal ice-sheets game, Scientific Reportsvolume, 7, 2078, https://doi.org/10.1038/s41598-017-02148-7, 2017. a, b, c, d, e, f
Nye, J. F.: The Flow Law of Ice from Measurements in Glacier Tunnels, Laboratory Experiments and the Jungfraufirn Borehole Experiment, P. Roy. Soc. A-Math. Phy., 219, 477–489, 1953. a
Onde, H.: La Maurienne et la Tarentaise; étude de Géographie physique, PhD thesis, Université de Grenoble, Switzerland, 1938. a, b
Paterson, W. S. B. and Budd, W. F.: Flow parameters for ice sheet modeling, Cold Reg. Sci. Technol., 6, 175–177, 1982. a
Patterson, T. and Kelso, N. V.: Natural Earth. Free vector and raster map data, available at: http://naturalearthdata.com, last access: 22 November 2017. a
Penck, A. and Brückner, E.: Die alpen im Eiszeitalter, Tauchnitz, Leipzig, 1909. a, b, c, d, e, f
Preusser, F.: Towards a chronology of the Late Pleistocene in the northern Alpine Foreland, Boreas, 33, 195–210, https://doi.org/10.1111/j.1502-3885.2004.tb01141.x, 2004. a, b, c, d, e, f, g
Preusser, F. and Schlüchter, C.: Dates from an important early Late Pleistocene ice advance in the Aare valley, Switzerland, Eclogae Geol. Helv., 97, 245–253, https://doi.org/10.1007/s00015-004-1119-4, 2004. a
Preusser, F., Geyh, M. A., and Schlüchter, C.: Timing of Late Pleistocene climate change in lowland Switzerland, Quaternary Sci. Rev., 22, 1435–1445, https://doi.org/10.1016/S0277-3791(03)00127-6, 2003. a
Preusser, F., Blei, A., Graf, H. R., and Schlüchter, C.: Luminescence dating of Würmian (Weichselian) proglacial sediments from Switzerland: methodological aspects and stratigraphical conclusions, Boreas, 36, 130–142, https://doi.org/10.1111/j.1502-3885.2007.tb01187.x, 2007. a
Preusser, F., Graf, H. R., Keller, O., Krayss, E., and Schlüchter, C.: Quaternary glaciation history of northern Switzerland, Quaternary Sci. J., 60, 282–305, https://doi.org/10.3285/eg.60.2-3.06, 2011. a, b
Rolland, C.: Spatial and Seasonal Variations of Air Temperature Lapse Rates in Alpine Regions, J. Climate, 16, 1032–1046, https://doi.org/10.1175/1520-0442(2003)016<1032:sasvoa>2.0.co;2, 2003. a, b
Schlüchter, C.: A non-classical summary of the Quaternary stratigraphy in the northern alpine foreland of Switzerland, Bulletin de la Société Neuchâteloise de Géographie, 32, 143–157, 1988. a
Schlüchter, C.: Fazies und Chronologie des letzteiszeitlichen Eisaufbaues im Alpenvorland der Schweiz, in: Klimageschichtliche Probleme der letzten 130000 Jahre, in: Klimageschichtliche Probleme der letzten 130 000 Jahre, edited by: Frenzel, B., G. Fischer Verlag, Stuttgart, 401–407, 1991. a
Schoof, C.: The effect of basal topography on ice sheet dynamics, Continuum Mech. Therm., 15, 295–307, https://doi.org/10.1007/s00161-003-0119-3, 2003. a
Seguinot, J.: Spatial and seasonal effects of temperature variability in a positive degree-day glacier surface mass-balance model, J. Glaciol., 59, 1202–1204, https://doi.org/10.3189/2013JoG13J081, 2013. a, b, c
Seguinot, J.: Numerical modelling of the Cordilleran ice sheet, PhD thesis, Stockholm University, available at: http://urn.kb.se/resolve?urn=urn:nbn:se:su:diva-106815, last access: 2014. a, b
Seguinot, J., Khroulev, C., Rogozhina, I., Stroeven, A. P., and Zhang, Q.: The effect of climate forcing on numerical simulations of the Cordilleran ice sheet at the Last Glacial Maximum, The Cryosphere, 8, 1087–1103, https://doi.org/10.5194/tc-8-1087-2014, 2014. a, b
Seguinot, J., Rogozhina, I., Stroeven, A. P., Margold, M., and Kleman, J.: Numerical simulations of the Cordilleran ice sheet through the last glacial cycle, The Cryosphere, 10, 639–664, https://doi.org/10.5194/tc-10-639-2016, 2016. a, b
Seguinot, J.: Alpine ice sheet glacial cycle simulations aggregated variables [Data set], Zenodo, available at: https://doi.org/10.5281/zenodo.1423160, 2018a.
Seguinot, J.: Alpine ice sheet glacial cycle simulations continuous variables [Data set], Zenodo, available at: https://doi.org/10.5281/zenodo.1423176, 2018b.
Seguinot, J.: Modelling last glacial cycle ice dynamics in the Alps, German National Library of Science and Technology (TIB) AV-Portal, available at: https://doi.org/10.5446/35164, 2018c. a
Shackleton, N. J. and Opdyke, N. D.: Oxygen isotope and palaeomagnetic stratigraphy of Equatorial Pacific core V28-238: Oxygen isotope temperatures and ice volumes on a 105 year and 106 year scale, Quaternary Res., 3, 39–55, https://doi.org/10.1016/0033-5894(73)90052-5, 1973. a
Spötl, C. and Mangini, A.: Stalagmite from the Austrian Alps reveals Dansgaard–Oeschger events during isotope stage 3:: Implications for the absolute chronology of Greenland ice cores, Earth Planet. Sc. Lett., 203, 507–518, https://doi.org/10.1016/S0012-821X(02)00837-3, 2002. a, b, c
Spötl, C., Reimer, P. J., and Göhlich, U. B.: Mammoths inside the Alps during the last glacial period: Radiocarbon constraints from Austria and palaeoenvironmental implications, Quaternary Sci. Rev., 190, 11–19, https://doi.org/10.1016/j.quascirev.2018.04.020, 2018. a
Strandberg, G., Brandefelt, J., Kjellstrom, E., and Smith, B.: High-resolution regional simulation of last glacial maximum climate in Europe, Tellus A, 63, 107–125, https://doi.org/10.1111/j.1600-0870.2010.00485.x, 2011. a, b
Stroeven, A. P., Fabel, D., Hättestrand, C., and Harbor, J.: A relict landscape in the centre of Fennoscandian glaciation: cosmogenic radionuclide evidence of tors preserved through multiple glacial cycles, Geomorphology, 44, 145–154, https://doi.org/10.1016/S0169-555X(01)00150-7, 2002. a
Suter, S., Laternser, M., Haeberli, W., Frauenfelder, R., and Hoelzle, M.: Cold firn and ice of high-altitude glaciers in the Alps: measurements and distribution modelling, J. Glaciol., 47, 85–96, https://doi.org/10.3189/172756501781832566, 2001. a
the PISM authors: PISM, a Parallel Ice Sheet Model, available at: http://www.pism-docs.org (last access: 7 March 2017), 2015. a, b
Tulaczyk, S., Kamb, W. B., and Engelhardt, H. F.: Basal mechanics of Ice Stream B, west Antarctica: 1. Till mechanics, J. Geophys. Res., 105, 463–481, https://doi.org/10.1029/1999jb900329, 2000. a, b, c, d, e
van Husen, D.: Zur quartären Entwicklung im Gailtal, in: Arbeitstagung der Geologischen Bundesanstalt, Geologische Bundesanstalt, Wien, 10–15, available at: http://www.zobodat.at/pdf/Arbeitstagungen-geologischen-Bundesanstalt_1985_0010-0015.pdf (last access: September 2018), 1985. a, b
van Husen, D.: Die Ostalpen in den Eiszeiten, Geologische Bundesanstalt, Wien, 1987. a, b, c, d, e
van Husen, D.: Chapter 2 – Quaternary Glaciations in Austria, in: Quaternary Glaciations – Extent and Chronology: A Closer Look, edited by: Ehlers, J., Gibbard, P. L., and Hughes, P. D., 15, 15–28, https://doi.org/10.1016/b978-0-444-53447-7.00002-7, 2011. a, b, c, d, e, f
Van Husen, D. and Reitner, J. M.: An Outline of the Quaternary Stratigraphy of Austria, E&G Quaternary Sci. J., 60, 366–387, https://doi.org/10.3285/eg.60.2-3.09, 2011. a
Venetz, I.: Mémoire sur les variations de la température dans les Alpes de la Suisse, 38 pp., 1821. a
Walcott, R. I.: Flexural rigidity, thickness, and viscosity of the lithosphere, J. Geophys. Res., 75, 3941–3954, https://doi.org/10.1029/JB075i020p03941, 1970. a
Windham, W. and Martel, P.: An account of the glacières or ice alps in Savoy, in two letters, one from an English gentleman to his friend at Geneva; the other from Peter Martel, engineer, to the said English gentleman, as laid before the Royal Society, London, UK, 1744. a
Winkelmann, R., Martin, M. A., Haseloff, M., Albrecht, T., Bueler, E., Khroulev, C., and Levermann, A.: The Potsdam Parallel Ice Sheet Model (PISM-PIK) – Part 1: Model description, The Cryosphere, 5, 715–726, https://doi.org/10.5194/tc-5-715-2011, 2011. a
Wirsig, C., Zasadni, J., Christl, M., Akçar, N., and Ivy-Ochs, S.: Dating the onset of LGM ice surface lowering in the High Alps, Quaternary Sci. Rev., 143, 37–50, https://doi.org/10.1016/j.quascirev.2016.05.001, 2016. a, b, c, d, e
Wohlfarth, B., Veres, D., Ampel, L., Lacourse, T., Blaauw, M., Preusser, F., Andrieu-Ponel, V., Kéravis, D., Lallier-Vergès, E., Björck, S., Davies, S. M., de Beaulieu, J.-L., Risberg, J., Hormes, A., Kasper, H. U., Possnert, G., Reille, M., Thouveny, N., and Zander, A.: Rapid ecosystem response to abrupt climate changes during the last glacial period in western Europe, 40–16 ka, Geology, 36, 407, https://doi.org/10.1130/G24600A.1, 2008. a, b, c
Wu, H. B., Guiot, J. L., Brewer, S., and Guo, Z. T.: Climatic changes in Eurasia and Africa at the last glacial maximum and mid-Holocene: reconstruction from pollen data using inverse vegetation modelling, Clim. Dynam., 29, 211–229, 2007. a, b, c
Ziemen, F. A., Hock, R., Aschwanden, A., Khroulev, C., Kienholz, C., Melkonian, A., and Zhang, J.: Modeling the evolution of the Juneau Icefield between 1971 and 2100 using the Parallel Ice Sheet Model (PISM), J. Glaciol., 62, 199–214, https://doi.org/10.1017/jog.2016.13, 2016. a
Lithosphere rigidity was computed using the erroneous formula, , in Mey et al. (2016). The correct formula is (Love, 1906). Using Young's modulus, Y=100 GPa, and the Poisson ratio, ν=0.25 (Mey et al., 2016), the consequence of this error is that the simulations effectively use an elastic thickness of the lithosphere of E=53.8 km instead of 50 km, which is well within uncertainties (Mey et al., 2016), thus introducing a % change in the length scale of bedrock deformation (Walcott, 1970).





