the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A key factor initiating surface ablation of Arctic sea ice: earlier and increasing liquid precipitation
Tingfeng Dou
Cunde Xiao
Jiping Liu
Wei Han
Zhiheng Du
Andrew R. Mahoney
Joshua Jones
Hajo Eicken
Snow plays an important role in the Arctic climate system, modulating heat transfer in terrestrial and marine environments and controlling feedbacks. Changes in snow depth over Arctic sea ice, particularly in spring, have a strong impact on the surface energy budget, influencing ocean heat loss, ice growth and surface ponding. Snow conditions are sensitive to the phase (solid or liquid) of deposited precipitation. However, variability and potential trends of rain-on-snow events over Arctic sea ice and their role in sea-ice losses are poorly understood. Time series of surface observations at Utqiaġvik, Alaska, reveal rapid reduction in snow depth linked to late-spring rain-on-snow events. Liquid precipitation is key in preconditioning and triggering snow ablation through reduction in surface albedo as well as latent heat release determined by rainfall amount, supported by field observations beginning in 2000 and model results. Rainfall was found to accelerate warming and ripening of the snowpack, with even small amounts (such as 0.3 mm recorded on 24 May 2017) triggering the transition from the warming phase into the ripening phase. Subsequently, direct heat input drives snowmelt, with water content of the snowpack increasing until meltwater output occurs, with an associated rapid decrease in snow depth. Rainfall during the ripening phase can further raise water content in the snow layer, prompting onset of the meltwater output phase in the snowpack. First spring rainfall in Utqiaġvik has been observed to shift to earlier dates since the 1970s, in particular after the mid-1990s. Early melt season rainfall and its fraction of total annual precipitation also exhibit an increasing trend. These changes of precipitation over sea ice may have profound impacts on ice melt through feedbacks involving earlier onset of surface melt.
Arctic sea ice has been experiencing rapid decline in both extent and thickness in recent decades (Stroeve et al., 2007, 2012; Comiso and Nishio, 2008). The 10 lowest sea ice extent anomalies on record have all occurred in recent decades. Sea-ice thinning trends (Kwok et al., 2009; Kwok and Untersteiner, 2011) have been associated with first-year sea ice replacing thicker multi-year sea ice (Maslanik et al., 2007, 2011; Giles et al., 2008). These changes make Arctic sea ice more susceptible to variations in thermodynamic forcings, increasing interannual variability (Kwok et al., 2009; Maslanik et al., 2007, 2011; Nghiem et al., 2007; Notz, 2009; Laxon et al., 2013). Snow over sea ice plays an important role in the growth and melt of Arctic sea ice (Maykut and Untersteiner, 1971; Maykut, 1986; Blazey et al., 2013; Perovich and Polashenski, 2012). Snow has a lower thermal conductivity and higher albedo (∼0.7–0.9 for wet to dry snow) than sea ice, which limits the absorption of solar energy by sea ice as well as by the ocean beneath sea ice (Eicken et al., 2004; Perovich and Polashenski, 2012). Screen and Simmonds (2012) showed that the fraction of Arctic summer precipitation occurring as snow has declined in recent decades due to lower-atmosphere warming, and this change of precipitation has likely contributed to the decrease in sea ice extent by reducing the area of snow-covered ice and the resulting surface albedo during summer.
In spring, changes in the amount of snow can either curb or foster sea ice melt. Thick snow helps maintain high surface albedos during the melt season (Eicken et al., 2004) and reduces solar heating of ice and upper ocean (Sturm et al., 2002). In contrast, thin snow melts back earlier in spring and promotes the formation of melt ponds (Eicken et al., 2004; Petrich et al., 2012), which absorb approximately 1.7 times more solar radiation than bare ice and approximately 5 times more than cold, snow-covered sea ice (Perovich et al., 2002; Perovich and Polashenski, 2012; Webster et al., 2014), accelerating ice decay and solar heating of the upper ocean in spring.
Spring snow depth on sea ice is very sensitive to the phase of precipitation. Solid precipitation increases snow depth, protecting sea ice from melt. Conversely, liquid precipitation heats the snowpack, changes snow grain morphology and lowers albedo, decreasing snow depth. Data from Operation IceBridge flights (2009–2013) indicate an average snow depth on Arctic sea ice of ∼20 cm (22.2 cm in the western Arctic and 14.5 cm in the Beaufort and Chukchi seas) (Webster et al., 2014), which renders the thin sea-ice snowpack particularly susceptible to earlier surface ablation and shorter duration as a result of liquid precipitation. An assessment based on 37 state-of-the-art climate models indicated that in the future rain is projected to become the dominant form of precipitation over the Arctic region (Bintanja and Andry, 2017). Rain-on-snow events over Arctic sea ice are likely to have profound impacts, particularly in late spring when the snowpack has warmed. However, to date no such investigation has been completed over Arctic sea ice.
In order to determine how liquid precipitation affects the surface ablation of sea ice and to assess its quantitative contribution to the reduction in snow depth over sea ice, here, we investigate the role of liquid precipitation in initiating snowmelt and the sea ice ablation season based on field measurements in the coastal Chukchi Sea. An energy balance model was adopted to help develop a mechanistic interpretation of the observations. The variability of rain-on-snow events over sea ice and the timing of first spring rain are analysed using long-term meteorological records available at Utqiaġvik, Alaska.
2.1 Data
2.1.1 Micrometeorological observations at the MB site
A snow and ice mass balance (MB) site has been deployed on undeformed landfast first-year ice in the Chukchi Sea north of Utqiaġvik since 1990s. At this location the ice is homogeneous, and it forms primarily through in situ freezing rather than advection and deformation and provides ice and snow data representative of level, undeformed ice (Druckenmiller and Haas, 2009). The relative humidity was measured with a Campbell CS500 instrument in 2013 and a Campbell HMP155A instrument from 2014 to 2016. Air temperature was measured 2 m above the ice with a shielded Campbell CS500 sensor in 2013 and with a Campbell HMP155A from 2014 to 2016. The shielded Rotronic HC2S3 that measured air temperature in 2017 also measured relative humidity. Wind direction and speed were measured by two R.M. Young and Campbell 5108-L anemometers, one 2.1 m above the initial snow surface and the other 4.1 m above the initial snow surface. Data were recorded every 15 min and transferred via FTP to the University of Alaska Fairbanks, where they were processed (Druckenmiller and Haas, 2009; Eicken et al., 2012). We used the data for 2013–2017 (https://arcticdata.io/catalog/\#view/doi:10.18739/A2D08X, last access: 15 March 2018).
2.1.2 Radiation, albedo, surface temperature and snow depth near the MB site
From April through June 2017, we conducted radiation and surface albedo measurements near the MB site. The distribution of snow depth at this location is the same as that at the MB site. Radiation was measured using a CNR4 net radiometer that records the upwelling and downwelling shortwave and longwave radiation. The surface albedo was derived from the upward solar radiation divided by the incident solar radiation. The surface temperature was measured with a SI-111 infrared radiometer. The sensors were fixed on a bracket 1.5 m above the snow surface. Data were recorded every 5 min and collected by LoggerNet 4.0 (CR1000). Snow depth was measured with a Campbell SR50 sonic ranger fixed to a mast extending through the ice. The accuracy is about ±1 cm.
2.1.3 Air temperature and precipitation at Utqiaġvik WSO AP station
The data analysed here comprise daily precipitation and snowfall from January 1952 to June 2017 for the Utqiaġvik Weather Service Office airport weather station (WSO AP), located near the coast of the Chukchi Sea at Utqiaġvik (available from the Alaska Climate Research Center; http://climate.gi.alaska.edu/acis_data, last access: 2 September 2018). The snowfall data are given as snow water equivalent (cm w.e.). The snowfall amount is subtracted from the total precipitation to obtain the rainfall amount (also in units of cm w.e.).
2.2 Methodology
2.2.1 Modelling of snow depth, snow density and snow water equivalent (SWE)
The surface energy balance for the snowpack overlying sea ice can be defined as
where Qnet is the net energy flux at the snowpack on sea ice, Q∗ is the net radiative flux, Qs is the turbulent sensible heat flux, Ql is the turbulent latent heat flux, C is the conductive heat flux and R is the heat input by rain. Each component of the surface energy budget is expressed in the unit W m−2. The net radiative flux is composed of the net shortwave and longwave components, which are derived from the observed incoming and outgoing radiative fluxes with a CNR4 net radiometer (see more details in the Data and methodology section). The sensible heat Qs and latent heat Ql were calculated by
where Vz is the mean wind speed (m s−1) in 1 h at a height z and ρa (unit: kg m−3) and cp (unit: J (kg K)−1) denote the air density and the specific heat capacity of air. rl is the vaporization enthalpy. (Ts−Ta) and (qs−qa) are the differences in temperature and specific humidity between the snow surface and atmosphere at the height z. The temperature and humidity are respectively expressed in the unit K and g m−3.
CH and CE are the bulk transfer coefficients estimated from a simple non-iterative algorithm (Launiainen and Chengm, 1995) based on the Monin–Obukhov similarity theory.
The conductive heat flux C was estimated as
where k is the thermal conductivity of snow in W m−1 K, and Ts is the snow surface temperature in K. The observed ice surface temperature Ti was applied in this study. Hs is snow depth in m. k varies with snow density according to the regression in Eqs. (2) and (2), as suggested by Sturm et al. (2002).
For heat input by rain, two settings need to be considered. If rain falls on snowpack that is at the freezing point,
where Cw is the heat capacity of water in J (kg K)−1, r is the rainfall rate (m s−1) and Tr is the rain temperature (K). Rain is cooled to the freezing point, giving up sensible heat to warm the snowpack.
If rain falls on a snowpack below the freezing point,
where Lm is the latent heat of fusion in J kg−1, and Tm is the freezing point in K. Rain first cools to the freezing point, giving up sensible heat. Thereafter the rain will freeze, releasing latent heat, which can heat the snowpack effectively.
Once the snowpack reaches the warming phase, the positive energy budget is used to melt snow. The amount of snowmelt ΔSWE (snow water equivalent in m) was estimated as
where Qnet is the net energy flux derived from Eq. (1), and ρw denotes water density in kg m−3.
The snow density changes were modelled based on
where C1 and C2 are empirical coefficients, which are 7.0 m−1 h−1 and 21.0 cm3 g−1 according to the field measurements in Yen et al. (1981). T0 is the freezing point temperature. Here, Δt is equal to 1 h.
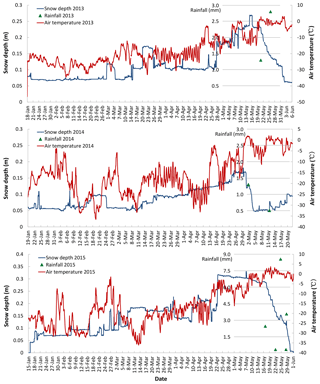
Figure 1Rainfall and variations in air temperature and snow depth recorded near Utqiaġvik, Alaska. The data were observed at the MB site on Chukchi Sea landfast ice between January and June in 2013, 2014 and 2015. Amount (mm w.e.) and timing of rainfall are indicated by blue triangles.
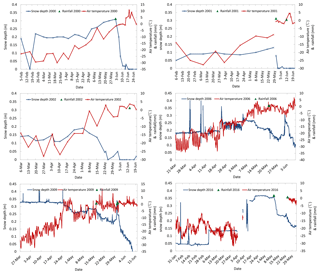
Figure 2Observed air temperature, snow depth and liquid precipitation over coastal Chukchi Sea ice in 2000, 2001, 2002, 2006, 2009, 2016.
The snow depth Hs was modelled by
where SWE is snow water equivalent in m, ρs is snow density in kg m−3, and SWEnew is new deposited snow in snow water equivalent (m). The density of new fallen snow ρsnew is 102 kg m−3 on average derived from the field measurement in Chukchi Sea 2017.
The energy required to reach the isothermal state was calculated according to [ciρw SWE (Tave−Tm)] by Dingman (2015), where CI is the heat capacity of snow or ice (2.1 kJ kg−1 ∘C−1), Tave is the average temperature of the snowpack, Tm is the freezing point of snow, ρw is the density of water, and SWE is snow water equivalent in m. The temperature profile of the snowpack used to track the timing of the isothermal state was measured with a CRREL-designed thermistor string employing Beaded Stream thermistors. The thermistors were spaced 2 cm apart and measure temperature with 0.1 ∘C accuracy.
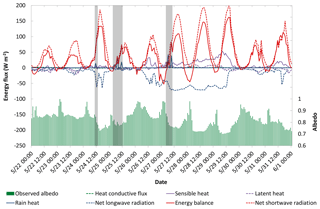
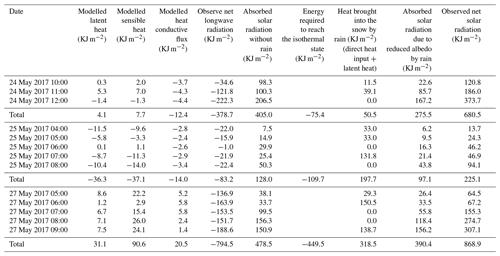
Figure 3Energy balance of snow over sea ice during the early stage of melt season. Observed net solar radiation, albedo, net longwave radiation and timing of rainfall from 22 May through 1 June 2017 (local time). Calculated sensible heat, latent heat, heat conductive flux and energy budget during the same period are also shown. Rain heat includes the heat that rain directly brings into the snowpack and the latent heat release when the rain freezes within the snowpack. Grey shading shows the timing of rainfall.

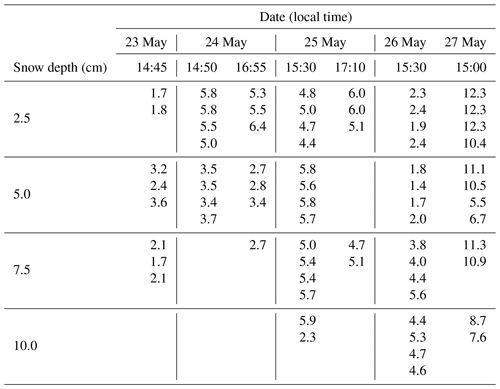
Figure 4Observed snow morphology at different depths of the snowpack over ice in the Chukchi Sea north of Utqiaġvik from 23 May through 27 May 2017. The reference ruler is 0.5 mm long.
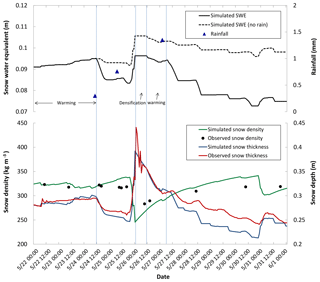
Figure 5Observed and modelled snow density, thickness and snow water equivalent (SWE) at different stages of snowmelt. A sensitivity experiment without rain was conducted for the same time period, and the corresponding SWE is also shown. Rainfall, snow density and depth were observed at the surface of Chukchi Sea landfast ice from 22 May through 1 June 2017. A detailed description of the ablation process is provided in the “Observations and model simulations of key processes” section.
2.2.2 Model experiments
Two experiments were conducted to quantitatively estimate the contribution of rain to snow ablation. In the control run, we applied the meteorological observations to drive the model and simulate the snow depth, snow density and SWE. These observations include wind, air temperature, relative humidity, snow surface temperature, upward and downward longwave radiation, incoming solar radiation, surface albedo, rainfall, snowfall, snow temperature and snow–ice interface temperature. The measured snow depth and snow density were used to validate the model results. In the sensitivity experiment, we excluded the impacts of rain by lowering albedo and eliminating the latent heat and sensible heat terms contributed by rainfall.
As observed in this study and previous studies, such as Perovich et al. (2002, 2017) and Perovich and Polashenski (2012), rain can decrease the surface albedo by ∼0.1 within a few hours. This impact on albedo is quite different from that of a gradual warming or melting process. The latter needs ∼10 days to reduce the albedo by the same amount (Perovich et al., 2002, 2017). In the sensitivity experiment, we derived an evolutionary sequence of albedo without rain based on a simplifying assumption, in which albedos are linearly extrapolated based on the observations of the previous 3 days using the method of Perovich et al. (2017) for the period 24 May–3 June (also see their Figs. 2 and 3). In contrast, the control experiment includes all impacts of rainfall on surface properties and fluxes and therefore draws on the observed albedo time series from the same period. The observed downwelling solar irradiance was applied to calculate the absorbed solar radiation with and without rain.
2.2.3 Significance testing
We calculated the significance value of a linear trend for first rainfall date, rainfall in May, total precipitation and rainfall : total precipitation ratio in May using Student's t test. The trend is significant when p≤0.05 with 95 % confidence.
Field measurements at a mass balance site (MB site) on landfast sea ice near Utqiaġvik, Alaska, in April–June from 2013 to 2015 revealed rapid declines in snow depth once non-freezing rain fell on the snow. Figure 1 shows the variations of snow depth and surface air temperature observed in 2013–2015. It appears that snow depth on sea ice started to decrease when air temperature rose above the freezing point (0∘). Snow depth then decreased sharply and persistently during subsequent days (6, 3 and 6 days for 2013, 2014 and 2015, respectively). The change in surface air temperature itself cannot explain such rapid reduction in snow depth since surface air temperature fluctuates above and below the freezing point at this time. Rather, the first non-freezing rain events of the year that were immediately followed by the rapid decrease in snow depth might be responsible for such a phenomenon. Our available observations from prior years at Utqiaġvik and in the ice pack of the Chukchi Sea corroborate these findings (Fig. 2) as do studies suggesting that the transition into the Arctic surface melt season is linked to pronounced synoptic events, rather than through gradual heating processes (Alt, 1987; Persson et al., 1997; Stone et al., 2002; Wang et al., 2005; Sharp and Wang, 2009; Persson and Ola, 2012).
A primary mechanism for the acceleration of surface melt and ablation is the rain-induced rapid lowering of surface albedo. In order to evaluate this impact, we conducted field measurements of surface albedo in conjunction with characterization of the state of the snow and ice cover on Chukchi Sea ice in April and June 2017. Observations showed that surface albedo decreased sharply on 24, 25 and 27 May by 0.12, 0.10 and 0.13, respectively, coinciding with the occurrence of rain-on-snow events (Fig. 3). The observed snow morphology (Fig. 4) and water content (Table 1) indicated significant melt of the snowpack after rainfall for these 3 days, corresponding to a decrease in snow depth (Fig. 5). Comparison with the earlier two warming events (15 and 18 May), with temperatures at or above the freezing point, demonstrates that the warming events alone did not result in such a rapid decrease in albedo but that liquid precipitation plays a key role. Consistently, two earlier studies also supported that a sharp drop in surface albedo by over 0.05 within a single day was associated with a rain-on-snow event, different from the gradual decline in surface albedo associated with seasonal surface warming and individual warming events (Perovich et al., 2002, 2017). Such rapid decrease in surface albedo may result in a significant increase in the absorbed shortwave flux. In addition, the rain can directly bring heat into the snow layer and heat the snowpack interior through the release of latent heat during refreezing of rainwater in the early stages of snow warming.
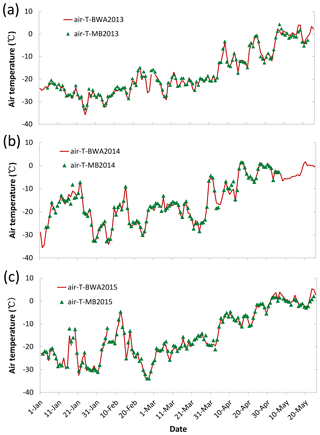
Figure 6Comparison of air temperature observed at WSO AP (Utqiaġvik Weather Service Office airport weather station) and the MB site during January–June 2013 (a), 2014 (b) and 2015 (c).
In order to quantitatively estimate the contribution of liquid precipitation towards rapid decreases in snow depth, we consider three basic snowmelt phases: warming, ripening and meltwater output phase (Dingman, 2015). For the warming phase, the absorbed energy raises the average snowpack temperature to the freezing point and the snowpack becomes isothermal. Only in an isothermal snowpack is the absorbed energy transformed effectively into snowmelt, initiating the snowpack ripening phase, which in turn leads into the meltwater output phase.
Based on our latest and most comprehensive field measurements, the surface energy budget and contribution from each component were estimated, to identify the dominant factors governing the warming phase of snowmelt during three key periods with rainfall occurrence. The first rainfall in 2017 was recorded as starting at 10:00 on 24 May (the average snow cover temperature was −0.7 ∘C). The observed snow temperature showed that the upper layers of the snowpack (16 cm) became isothermal after 2 h. The observed snow particle size and water content data indicate that the upper 10 cm began to melt immediately (Fig. 4 and Table 1). Interestingly, the modelled shortwave radiation absorbed by the snow layer without rainfall (405 KJ m−2) could offset the heat loss (−391 KJ m−2) from longwave radiative loss and heat conduction, but the residual – which includes latent and sensible heat – was too small to increase the temperature of the snow layer to the freezing point. During this period, rain changed the energy balance, initiating the warming phase of snowmelt in two ways: (1) increasing the absorption of solar radiation (275.47 KJ m−2) by lowering surface albedo and (2) transferring heat into the snowpack. At the same time, such rain events may exceed the storage capacity of water in the snowpack since the snow temperature was still low at this time. As a result, water drains downward, forming ice layers in the lower part of the snowpack and releasing latent heat (contributing in total 50.5 KJ m−2). Therefore, rainfall is believed to be the main factor in rapidly warming the snow layer to an isothermal state in this case.
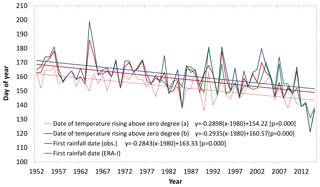
Figure 7Timing of air temperature exceeding 0∘ for the first time and the timing of first rainfall in spring at the WSO AP site, 1952–2015. The dashed red line (a) corresponds to the first instance of air temperature above 0 ∘C. The solid red line (b) indicates the first warming event continuing for at least 4 days. p denotes the significance value of the linear trend.
From the night of 24 May to the morning of 25 May, the snow temperature fell below the freezing point (−1.0 ∘C), and then rainfall occurred at 04:00 on 25 May. The snow temperature observations demonstrated that the snow layer reached an isothermal state after 5 h. During this period, the solar radiation absorbed by the snow cover would have been 128 KJ m−2 if there were no rainfall, which is not enough to make up for the total energy loss (171 KJ m−2) mainly from the longwave loss (−83 KJ m−2) and from sensible (−36 KJ m−2) and latent heat transfer (−37 KJ m−2) and heat conduction (−14 KJ m−2). Due to the occurrence of rainfall and the resulting albedo reduction, the snowpack absorbed an additional 97 KJ m−2 of solar radiation, and the rain also brought 198 KJ m−2 into the snowpack, mainly through latent heat release and direct heat input. Most of the rain-induced energy transfer was used to warm the snowpack; once the snowpack reached the warming phase, the remaining energy was used to melt the snow further, pushing the snowpack into ripening phase.
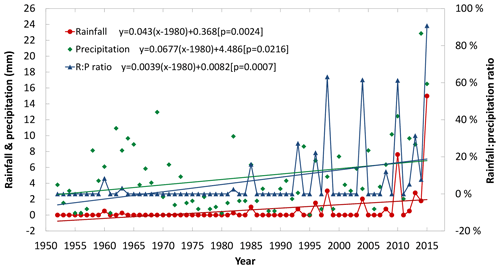
Figure 8The variation trend of rainfall, total precipitation and R:P ratio at Utqiaġvik for May, 1952–2015. p denotes the significance value of the linear trend.
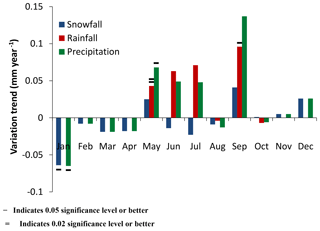
Figure 9The variation trends of rainfall, snowfall and precipitation for each month at Utqiaġvik from January 1952 to December 2015. The trend is characterized by the slope of the linear regression equation of the time series (− indicates 0.05 significance level or better; = indicates 0.02 significance level or better).
A heavy snowfall occurred during the evening of 25 May through the morning of 26 May. A constant SWE and reduced snow thickness indicated that there was significant snow densification during the daytime on 26 May, which was confirmed by the increase in snow density (Fig. 5). From the evening of 26 May to the morning of 27 May, the snow temperature decreased to −2.9 ∘C. Subsequently, rainfall occurred at 05:00 on 27 May, and the entire snowpack reached an isothermal state within 5 h after the rainfall, as observed in the snow temperature record. During this period, the heat loss from longwave radiation was larger than other components of the heat budget (−795 KJ m−2). The absorbed solar radiation (479 KJ m−2), latent heat (31 KJ m−2) and sensible heat (91 KJ m−2) were far from enough to offset this part of the energy budget in the absence of rainfall. The rainfall contributed 390 KJ m−2 to the energy balance by reducing the surface albedo and contributed 318 KJ m−2 by bringing heat directly into the snowpack and releasing latent heat (the latter accounted for the main contribution).
The model results shown above demonstrate that liquid precipitation can lead to completion of the warming phase within several hours, subsequently initiating the melt season (Fig. 5 and Table 2). Once the warming phase is reached, the remaining energy is used to further melt the snow, producing significant meltwater flow and contributing to snowpack ripening, together with the subsequent absorption of solar radiation (some of which was also contributed by rain-on-snow). According to Table 2, the remaining energy was 377 KJ m−2 on 24 May. For this period, 534 KJ m−2 was needed to push the snowpack into the ripening phase. The remaining energy contributed substantially to attainment of the ripening phase, which lasted only briefly on 24 May due to rapid warming; on 25 May, the remaining energy was 143 KJ m−2, and on 27 May, it was 86 KJ m−2. Subsequently, the absorbed energy drove further snowmelt, with water content of the snowpack increasing until meltwater output occurred, with an associated rapid decrease in snow depth. If rainfall occurs during the ripening phase, it increases water content in the snow layer, pushing the snowpack into the meltwater output phase. This is confirmed by the model simulations showing that SWE decreased significantly within a few hours after each rainfall. In the absence of rainfall, warming is mostly sluggish, and the snow depth reduction is much more gradual as snowmelt proceeds, as was the case in 2002 (Fig. 2). A comparison of modelled SWE for the cases with and without rainfall demonstrates that in the case in which the longwave radiant flux is kept consistent with the observations, in the absence of rain, the snowpack does not undergo such rapid ablation (Fig. 5).
In addition to the contribution of surface ablation in reducing snow depth, the physical properties of the snow itself will affect the decrease in snow depth to a certain extent when ablation begins. For example, brine may collect at the surface of the sea ice cover as a result of expulsion through surface cracks (Tucker III et al., 1992) and will wick into the bottom layers of the snowpack through capillary action. Consequently, the base of the snowpack can consist of such brine-wetted snow (Martin, 1979), with liquid water present even at low temperatures due to the high salinity of the brine (Geldsetzer et al., 2009). Previous work in the Arctic, including at the location studied here, has established that for Arctic snowpack (in contrast with the Antarctic) typically only the lowermost centimetres of the snowpack exhibit higher salt content (Domine et al., 2004; Douglas et al., 2012). Therefore the presence of brine-wetted snow may accelerate the transition of the lowermost snow layers into the ripening phase during ablation but does not impact the onset of melt in the surface layers of the snowpack.
In addition, in our field work, we found depth hoar to be commonly present at the bottom of the snowpack. Depth hoar is a typical stratigraphic element of the basal layers of the Utqiaġvik snowpack during the spring season, widely confirmed in previous studies (e.g. Hall et al., 1986; Domine et al., 2012). Depth hoar is conducive to discharge of meltwater and subsidence of the snow cover surface, thereby promoting rapid reduction in snow depth. In theory, the presence of both depth hoar and brine-wetted snow supports the rapid reduction of snow depth through the process outlined in this study, though further observations are required to establish the relative importance of this process.
Having demonstrated the profound impact of rainfall on snow depth and ablation, we explore variability in the timing of first rain-on-snow events since the start of the available record. Due to the lack of long-term continuous observations over sea ice, we employ observations from Utqiaġvik WSO AP station, which is close to the MB site. Precipitation and surface air temperature have been measured at WSO AP since 1902 with large data gaps prior to 1952. Here we use air temperature and precipitation data from 1952 to 2017. A comparison of surface air temperature between WSO AP and the MB site shows close correspondence (Fig. 6). The amount of liquid precipitation was not recorded at the MB site, but we did record the timing of rainfall on sea ice or at the laboratory near the MB site from April through June in the field expedition of 2015 and 2017. This timing is in good agreement with the records from WSO AP. Hence, meteorological conditions at WSO AP are representative of the MB site.
As shown in Fig. 7, the first rain-on-snow events of the year have been shifted to earlier dates over the past 60 years (2.8 days decade−1, P<0.01). This trend towards earlier spring rainfall has been more pronounced since the early 2000s (26.9 days decade−1 during 2000–2015, P<0.01), which is consistent with the accelerated decline of Arctic sea ice since the early 2000s. Meanwhile, the timing of surface air temperature rising above the freezing point has also been occurring earlier for the past 60 years (3.0 days decade−1; P<0.01; Fig. 7). There is a clear relationship between the timing of first rainfall and the timing of air temperature rising above the freezing point (r=0.66). After removing the linear trend, the correlation is 0.57 (p<0.01). On average, the timing of air temperature rising above the freezing point is earlier than the first rainfall event by 9.1 days, suggesting that air temperature exceeding the freezing point is not in and of itself a driver of rain-on-snow events. Further analysis indicates that in some years (32 %), after the warming events continued for 1–2 days, air temperature dropped again without occurrence of recorded rainfall. Similarly, warming events of 3 days' duration without rainfall account for 21 % of all cases. Hence, we recalculate the timing of warming events that persisted for at least 4 days. Results show that these two measures of spring warming are highly positively correlated (r=0.96). After removing the linear trend, the correlation is still strong (r=0.95, p<0.01), suggesting that the year-to-year variability of the timing of first spring rainfall is closely tied to the timing of persistent warming events (Fig. 7), which might be associated with large-scale weather events.
Prior to the mid-1990s there was almost no rainfall in May (Fig. 8). Since then, the amount of rainfall has increased, especially in the past 10 years. Rainfall amount in May has been increasing significantly over the past 60 years (Fig. 9), with a linear trend of 0.43 mm decade−1 during 1952–2015 (p<0.01) and 1.4 mm decade−1 since the mid-1990s (p<0.01). By contrast, the total precipitation did not change significantly before and after the mid-1990s but has increased substantially over the past few years (Fig. 8). The trend towards higher ratios of rain : total precipitation (R:P ratio) in May has been significant over the past 60 years (0.04 per decade; p<0.01; Fig. 8), especially after the mid-1990s (0.09 per decade; p<0.01).
Snow on sea ice strongly impacts the surface energy budget, driving ocean heat loss, ice growth and surface ponding. While the role of snow depth and snowfall variations is well understood, this study demonstrated that rain-on-snow events are a critical factor in initiating the onset of surface melt over Arctic sea ice, primarily through reduction in surface albedo as well as latent heat release. By pushing the snowpack into the isothermal, ripening and meltwater output phase, liquid precipitation can sharply reduce snow depth and initiate the onset of rapid surface ablation. The increases in downwelling longwave fluxes through cloud warming associated with rainfall events contribute to warming of the snowpack to the melting point but are not sufficient to drive the temperature of the entire snow layer into an isothermal state on short timescales. In contrast, the occurrence of liquid precipitation can induce a quick transition of the snow temperature from diurnally varying to an isothermal state. The observations at Utqiaġvik and in the offshore Chukchi Sea ice pack suggest that at least in some years rain-on-snow events act as an effective, mostly irreversible trigger for the transition into the surface ablation season. In cases in which melt onset occurred in the absence of rain, increases in downward longwave fluxes largely offset the longwave radiation heat loss of snow and are thus key to melt initiation (Mortin et al., 2016). However, as shown from our observations and model results, snowmelt triggered by increases in net longwave radiation is much slower than that driven by liquid precipitation. This study deepens the understanding of the trigger mechanism of sea ice ablation, which is helpful in improving the modelling and seasonal prediction of Arctic sea ice extent.
This study assembles process studies and long-term observations at an important coastal site in North America for the first time, showing that onset of spring rainfall over sea ice has shifted to earlier dates since the 1970s, in particular since the mid-1990s. Early melt season rainfall and its fraction of total annual precipitation also exhibit an increasing trend. Based on the observational evidence and model results, we speculate that earlier and increasing liquid precipitation leads to earlier and more rapid melt of snowpack over sea ice, allowing for earlier formation of melt ponds. This strengthens the ice–albedo feedback, leading to greater ice mass loss in summer (Perovich et al., 1997; Stroeve et al., 2014), with the resulting thinner ice in turn reducing the ice pack in September (Notz, 2009). This inference needs further confirmation in future studies.
The micrometeorological observations (air temperature, relative humidity) at the MB site data can be accessed at https://doi.org/10.18739/A2D08X (Eicken, 2016). Air temperature and precipitation at Utqiaġvik WSO AP station are available from the Alaska Climate Research Center at http://climate.gi.alaska.edu/acis_data (last access: 2 September 2018).
TD, CX, JL and HE jointly conceived the study and wrote the paper with additional input from WH, ZD, AM and JJ. AM, HE and TD conceived field measurements and generated in situ data and associated products used in this study. TD performed the analyses. All of the authors discussed the results and contributed to interpretations.
The authors declare that they have no conflict of interest.
This study is funded by the National Key Research and Development Program of China (2018YFC1406103, 2018YFA0605901), the National Nature Science Foundation of China (NSFC 41425003 and 41401079), the key project of CAMS “Research on the key processes of cryospheric rapid changes” (KJZD-EW-G03-04) and the Climate Program Office, NOAA, U.S. Department of Commerce (NA15OAR4310163 and NA14OAR4310216). MB site data at Utqiaġvik were collected through support of the U.S. National Science Foundation, grant PLR- 0856867. We thank Chris Polashenski and Nicholas Wright for providing the snow temperature profile data at the MB site in 2017, funded under NSF grant ARC-1603361, the “Snow, Wind and Time” project.
This paper was edited by John Yackel and reviewed by three anonymous referees.
Alt, B. T.: Developing synoptic analogs for extreme mass balance conditions on Queen Elizabeth Island ice caps, J. Clim. Appl. Meteor., 26, 1605–1623, 1987.
Bintanja, R. and Andry, O.: Towards a rain-dominated Arctic, Nat. Clim. Change., 7, 263–267, 2017.
Blazey, B. A., Holland, M. M., and Hunke, E. C.: Arctic Ocean sea ice snow depth evaluation and bias sensitivity in CCSM, The Cryosphere, 7, 1887–1900, https://doi.org/10.5194/tc-7-1887-2013, 2013.
Comiso, J. C. and Nishio, F.: Trends in the sea ice cover using enhanced and compatible AMSR-E, SSM/I, and SMMR data, J. Geophys. Res., 113, C02S07, https://doi.org/10.1029/2007JC004257, 2008.
Dingman, S. L.: Physical hydrology, 3rd edition, Waveland Press, Inc. 223–226, 2015.
Domine, F., Sparapani, R., Ianniello, A., and Beine, H. J.: The origin of sea salt in snow on Arctic sea ice and in coastal regions, Atmos. Chem. Phys., 4, 2259–2271, https://doi.org/10.5194/acp-4-2259-2004, 2004.
Domine, F., Gallet, J. C., Bock, J., and Morin, S.: Structure, specific surface area and thermal conductivity of the snowpack around Barrow, Alaska, J. Geophys. Res., 117, D00R14, https://doi.org/10.1029/2011JD016647, 2012.
Douglas, T. A., Domine, F., Barret, M., Anastasio, C., Beine, H. J., Bottenheim, J., Grannas, A., Houdier, S., Netcheva, S., Rowland, G., Staebler, R., and Steffen, A.: Frost flowers growing in the Arctic ocean-atmosphere-sea ice-snow interface: 1. Chemical composition, J. Geophys. Res., 117, D00R09, https://doi.org/10.1029/2011JD016460, 2012.
Druckenmiller, M. L. and Haas, C.: Integrated Ice Observation Programs, Book Chapter, Sea-Ice Handbook, edited by: Eicken, H., University of Alaska Press, 2009.
Eicken, H.: Automated ice mass balance site (SIZONET), Arctic Data Center, https://doi.org/10.18739/A2D08X, 2016.
Eicken, H., Grenfell, T. C., Perovich, D. K., Richter-Menge, J. A., and Frey, K.: Hydraulic controls of summer Arctic pack ice albedo, J. Geophys. Res., 109, C08007, https://doi.org/10.1029/2003JC001989, 2004.
Eicken, H., Gradinger, R., Heinrichs, T., Johnson, M. A., Lovecraft, A. L., and Kaufman, M.: Automated ice mass balance site (SIZONET), UCAR/NCAR – CISL – ACADIS, Dataset, https://doi.org/10.5065/D6MW2F2H, 2012.
Geldsetzer, T., Langlois, A., and Yackel, J. J.: Dielectric properties of brine-wetted snow on first-year sea ice, Cold Reg. Sci. Technol., 58, 47–56, 2009.
Giles, K. A., Laxon, S. W., and Ridout, A. L.: Circumpolar thinning of Arctic sea ice following the 2007 record ice extent minimum, Geophys. Res. Lett., 35, L22502, https://doi.org/10.1029/2008GL035710, 2008.
Hall, D. K., Chang, A. T. C., and Foster, J. L.: Detection of the depth-hoar layer in the snow-pack of the Arctic coastal plain of Alaska, U.S.A, using satellite data, J. Glaciol., 32, 87–94, 1986.
Kwok, R. and Untersteiner, N.: The thinning of Arctic sea ice, Phys. Today, 64, 36–41, 2011.
Kwok, R., Cunningham, G. F., Wensnahan, M., Rigor, I., Zwally, H. J., and Yi, D.: Thinning and volume loss of the Arctic Ocean sea ice cover: 2003–2008, J. Geophys. Res., 114, C07005, https://doi.org/10.1029/2009JC005312, 2009.
Launiainen, J. and Chengm B. A.: simple non-iterative algorithm for calculating turbulent bulk fluxes in diabatic conditions over water, snow/ice and ground surface, Rep. Ser. Geophys., 33, p. 16, 1995.
Laxon, S. W., Giles, K. A., Ridout, A. L., Wingham, D. J., Willatt, R., Cullen, R., Kwok, R., Schweiger, A., Zhang, J., Haas, C., Hendricks, S., Krishfield, R., Kurtz, N., Farrell, S., and Davidson, M.: CryoSat-2 estimates of Arctic sea ice thickness and volume, Geophys. Res. Lett., 40, 732–737, https://doi.org/10.1002/grl.50193, 2013.
Martin, S.: A field study of brine drainage and oil entrapment in first-year sea ice, J. Glaciol., 22, 473–502, 1979.
Maslanik, J., Drobot, S., Fowler, C., Emery, W., and Barry, R.: On the Arctic climate paradox and the continuing role of atmospheric circulation in affecting sea ice conditions, Geophys. Res. Lett., 34, L03711, https://doi.org/10.1029/2006GL028269, 2007.
Maslanik, J., Stroeve, J., Fowler, C., and Emery, W.: Distribution and trends in Arctic sea ice age through spring 2011, Geophys. Res. Lett., 38, L13502, https://doi.org/10.1029/2011GL047735, 2011.
Maykut, G. A.: The surface heat and mass balance, in: The geophysics of sea ice, edited by: Untersteiner, N., New York, Plenum Press, 395–463, 1986.
Maykut, G. A. and Untersteiner, N.: Some results from a time dependent thermodynamic model of sea ice, J. Geophys. Res., 76, 1550–1575, 1971.
Mortin, J., Svensson, G., Graversen, R. G., Kapsch, M. L., Stroeve, J. C., and Boisvert, L. N.: Melt onset over Arctic sea ice controlled by atmospheric moisture transport, Geophys. Res. Lett., 43, 6636–6642, 2016.
Nghiem, S. V., Rigor, I. G., Perovich, D. K., Clemente-Colón, P., Weatherly, J. W., and Neumann, G.: Rapid reduction of Arctic perennial sea ice, Geophys. Res. Lett., 34, L19504, https://doi.org/10.1029/2007GL031138, 2007.
Notz, D.: The future of ice sheets and sea ice: Between reversible retreat and unstoppable loss, P. Natl. Acad. Sci. USA, 106, 20590–20595, 2009.
Perovich, D. K. and Polashenski, C.: Albedo evolution of seasonal Arctic sea ice, Geophys. Res. Lett., 39, L08501, https://doi.org/10.1029/2012GL051432, 2012.
Perovich, D. K., Bruce, C. E., and Richter-Menge, J. A.: Observations of the annual cycle of sea ice 824 temperature, Geophys. Res. Lett., 24, 555–558, 1997.
Perovich, D. K., Grenfell, T. C., Light, B., and Hobbs, P. V.: Seasonal evolution of the albedo of multiyear Arctic sea ice, J. Geophys. Res., 107, 8044, https://doi.org/10.1029/2000JC000438, 2002.
Perovich, D., Polashenski, C., Arntsen, A., and Stwertka, C.: Anatomy of a late spring snowfall on sea ice, Geophys. Res. Lett., 44, 2802–2809, https://doi.org/10.1002/2016GL071470, 2017.
Persson, P. and Ola, G.: Onset and end of the summer melt season over sea ice: thermal structure and surface energy perspective from SHEBA, Clim. Dynam., 39, 1349–1371, 2012.
Persson, P., Ola, G., Ruffieux, D., and Fairall, C. W.: Recalculations of pack ice and lead surface energy budgets during LEADEX 92, J. Geophys. Res., 102, 25085–25089, 1997.
Petrich, C., Eicken, H., Polashenski, C. M., Sturm, M., Harbeck, J. P., Perovich, D. K., and Finnegan, D. C.: Snow dunes: A controlling factor of melt pond distribution on Arctic sea ice, J. Geophys. Res., 117, C09029, https://doi.org/10.1029/2012JC008192, 2012.
Screen, J. A. and Simmonds, I.: Declining summer snowfall in the Arctic: Causes, impacts and feedbacks, Clim. Dynam., 38, 2243–2256, 2012.
Sharp, M. and Wang, L.: A five-year record of summer melt on Eurasian Arctic ice caps, J. Climate, 22, 133–145, 2009.
Stone, R. S., Dutton, E. G., Harris, J. M., and Longenecker, D.: Earlier spring snowmelt in northern Alaska as an indicator of climate change, J. Geophys. Res., 107, 4089, https://doi.org/10.1029/2000JD000286, 2002.
Stroeve, J., Holland, M. M., Meier, W., Scambos, T., and Serreze, M.: Arctic sea ice decline: Faster than forecast, Geophys. Res. Lett., 34, L09501, https://doi.org/10.1029/2007GL029703, 2007.
Stroeve, J. C., Holland, M. M., Kay, J. E., Malanik, J., and Barrett, A. P.: The Arctic's rapidly shrinking sea ice cover: A research synthesis, Clim. Change, 110, 1005–1027, 2012.
Stroeve, J. C., Markus, T., Boisvert, L., Miller, J., and Barrett, A.: Changes in Arctic melt season and implications for sea ice loss, Geophys. Res. Lett., 41, 1216–1225, 2014.
Sturm, M., Perovich, D. K., and Holmgren, J.: Thermal conductivity and heat transfer through the snow on the ice of the Beaufort Sea, J. Geophys. Res., 107, 8043, https://doi.org/10.1029/2000JC000409, 2002.
Tucker III, W. B., Perovich, D. K., Gow, A. J., Weeks, W. F., and Drinkwater, M. R.: Physical properties of sea ice relevant to remote sensing, in: Microwave Remote Sensing of Sea Ice, edited by: Carsey, F., Geophysical Monograph, American Geophysical Union, 9–28, Chapter 2, 1992.
Wang, L., Sharp, M. J., Rivard, B., Marshall, S., and Burgess, D.: Melt season duration on Canadian Arctic ice caps, 2000–2004, Geophys. Res. Lett., 32, L19502, https://doi.org/10.1029/2005GL023962, 2005.
Webster, M. A., Rigor, I., Nghiem, S. V., Kurtz, N. T., Farrell, S. L., Perovich, D. K., and Sturm, M.: Interdecadal changes in snow depth on Arctic sea ice, J. Geophys. Res., 119, 5395–5406, https://doi.org/10.1002/2014JC009985, 2014.
Yen, Y.: Review of thermal properties of snow, ice and sea ice, US Army Cold Regions Research and Engineering Laboratory, Report 81–10, Hanover, NH, USA, 1981.
- Abstract
- Introduction
- Data and methodology
- Observed evidence of rapid reduction in snow depth associated with liquid precipitation
- Observations and model simulations of key processes
- Variability of rain-on-snow events
- Discussion and conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Review statement
- References
- Abstract
- Introduction
- Data and methodology
- Observed evidence of rapid reduction in snow depth associated with liquid precipitation
- Observations and model simulations of key processes
- Variability of rain-on-snow events
- Discussion and conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Review statement
- References