the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Scaling of instability timescales of Antarctic outlet glaciers based on one-dimensional similitude analysis
Anders Levermann
Johannes Feldmann
Recent observations and ice-dynamic modeling suggest that a marine ice-sheet instability (MISI) might have been triggered in West Antarctica. The corresponding outlet glaciers, Pine Island Glacier (PIG) and Thwaites Glacier (TG), showed significant retreat during at least the last 2 decades. While other regions in Antarctica have the topographic predisposition for the same kind of instability, it is so far unclear how fast these instabilities would unfold if they were initiated. Here we employ the concept of similitude to estimate the characteristic timescales of several potentially MISI-prone outlet glaciers around the Antarctic coast. Our results suggest that TG and PIG have the fastest response time of all investigated outlets, with TG responding about 1.25 to 2 times as fast as PIG, while other outlets around Antarctica would be up to 10 times slower if destabilized. These results have to be viewed in light of the strong assumptions made in their derivation. These include the absence of ice-shelf buttressing, the one-dimensionality of the approach and the uncertainty of the available data. We argue however that the current topographic situation and the physical conditions of the MISI-prone outlet glaciers carry the information of their respective timescale and that this information can be partially extracted through a similitude analysis.
- Article
(4584 KB) -
Supplement
(37482 KB) - BibTeX
- EndNote
Sea-level rise poses a future challenge for coastal regions worldwide (IPCC, WG II, 2014). The contribution from mass loss of the West Antarctic Ice Sheet has been increasing over the last 2 decades (Medley et al., 2014; The IMBIE team, 2018). Large parts of the Antarctic Ice Sheet rest on a retrograde marine bed, i.e., on a bed topography that lies below the current sea level and is downsloping inland (Bentley et al., 1960; Ross et al., 2012; Cook and Swift, 2012; Fretwell et al., 2013). This topographic situation makes these parts of the ice sheet prone to a so-called marine ice-sheet instability (MISI; Weertman, 1974; Mercer, 1978; Schoof, 2007; Pattyn, 2018). Currently, this kind of instability constitutes a large uncertainty in projections of future sea-level rise (IPCC, WG I, 2013; Joughin and Alley, 2011; Huybrechts et al., 2011; Golledge et al., 2015; Winkelmann et al., 2015; DeConto and Pollard, 2016; Pattyn et al., 2018): if the grounding line (that separates grounded from floating ice) enters a region of retrograde bed slope, a positive ice-loss feedback can be initiated. Resulting self-sustained retreat, acceleration and discharge of the ice sheet can be hindered by the buttressing effect of ice shelves and topographic features (Dupont and Alley, 2005; Goldberg et al., 2009; Gudmundsson et al., 2012; Favier et al., 2012; Asay-Davis et al., 2016) or strong basal friction (Joughin et al., 2009; Ritz et al., 2015).
The ongoing retreat of two major outlets of West Antarctica, Pine Island Glacier (PIG) and Thwaites Glacier (TG), initiated by warm-water entrainment into their ice-shelf cavities and resulting basal melting (Jenkins et al., 2010; Pritchard et al., 2012; Paolo et al., 2015; Shean et al., 2018), is pointing toward a developing MISI (Rignot et al., 2014; Mouginot et al., 2014; Konrad et al., 2018; Favier et al., 2014; Joughin et al., 2014; Seroussi et al., 2017) with the potential of raising the global sea level by more than 3 m (Bamber et al., 2009; Feldmann and Levermann, 2015). Whether the observed retreat indeed marks the start of a MISI or is a temporally limited response to oceanic variability still requires further studies (Hillenbrand et al., 2017; Smith et al., 2017; Jenkins et al., 2018). Similar warm-water exposition might apply to other Antarctic ice shelves in the future (Hellmer et al., 2012; Timmermann and Hellmer, 2013; Greene et al., 2017), bearing the potential to trigger unstable grounding-line retreat. It has been demonstrated that East Antarctica's Wilkes Subglacial Basin (WSB), would, once destabilized, contribute by 3–4 m to the global sea level (Mengel and Levermann, 2014). The marine part of the adjacent Aurora Subglacial Basin stores ice of around 3.5 m sea-level equivalent (Greenbaum et al., 2015). Other studies investigated the response of the Filchner-Ronne tributaries to enhanced melting (Wright et al., 2014; Thoma et al., 2015; Mengel et al., 2016) and suggest that instability might not unfold there, possibly due to the stabilizing buttressing effect of the large ice shelf and narrow bed troughs (Dupont and Alley, 2005; Goldberg et al., 2009; Gudmundsson et al., 2012). In total, the marine catchment basins of Antarctica that are connected to the ocean store ice masses of about 20 m sea-level equivalent (Fig. A1). Besides the question of whether local instabilities are already triggered, or will be triggered in the future, the question about which timescale a potentially unstable retreat would evolve if it had been initiated still remains. Naturally, numerical ice-sheet models are used to investigate these instabilities.
Here we try to contribute information using a different approach which is based the concept of similitude (Buckingham, 1914; Rayleigh, 1915; Macagno, 1971; Szücs, 1980). To this end the presented method combines observational and model data with a similarity analysis of the governing equations for shallow ice-stream flow. This similarity analysis has been carried out in previous work (Feldmann and Levermann, 2016), yielding scaling laws that determine how the geometry, the timescale, and the involved physical parameters for ice softness, surface mass balance and basal friction have to relate in order to satisfy similitude between different ice sheets. The approach is an analogy to, for example, the derivation of the Reynold's number (Reynolds, 1883) from the Navier–Stokes equation (Kundu et al., 2012), which can provide a scaling law that assures similar flow patterns of a fluid (laminar or turbulent) under variation of its characteristic geometric dimension, velocity and viscosity. In our previous paper we showed that the ice-sheet scaling behavior predicted according to the analytically derived scaling laws agrees with results from idealized three-dimensional, numerical simulations. In particular, this included the prediction of MISI-evolution timescales over a range of 3 orders of magnitude for different ice-sheet configurations respecting ice-sheet similarity. In the present study we take the next step and apply these scaling laws to the real world, aiming to infer relative response times to potential destabilization of 11 MISI-prone Antarctic outlets, based on their dynamic and geometric similarity (ice streams on marine, landward downsloping bed topography). This approach has the disadvantage of reduced dynamic complexity compared to numerical modeling but the advantage of being based on the observed ice-sheet configuration, which is generally not the case for an ice-sheet simulation.
Our approach is based on the fact that the currently observed shape of the considered Antarctic outlet glaciers represents the balance of the different forces that act on the ice, that is, the balance of the forces caused by the bed and ice topography, the surface mass balance, and the frictional forces from the ice interaction with itself and its surrounding. This static situation carries the information for the initial ice-sheet response after a potential destabilization. The scaling laws used to infer these response timescales come out of a similitude analysis of (1) the shallow-shelf approximation (SSA; e.g., as described by Morland, 1987; MacAyeal, 1989) of the Stokes stress balance and (2) mass conservation (Greve and Blatter, 2009).
The SSA is a simplified version of the Stokes stress balance, accounting for the case of membrane stresses dominating over vertical shear stresses. It is thus a suitable representation of the plug-like ice flow observed close to the grounding lines of the ice streams analyzed here. The equation of mass conservation provides the time evolution of the ice thickness, being determined by the horizontal ice-flux divergence and the surface mass balance.
The derivation of the scaling laws from these two equations is presented in full detail in Feldmann and Levermann (2016) and thus shall be outlined only very briefly here: in their dimensionless form the SSA and the equation of mass conservation together have three independent numbers, analogous to the Reynolds number in the Navier–Stokes equation (Reynolds, 1883). If each of these three numbers is the same for topographically similar situations (i.e., ice streams on retrograde bed) the solution of the ice-dynamical equations will be similar, satisfying three independent scaling laws (one for each dimensionless number). These numbers and thus the scaling laws are combinations of parameters or scales of characteristics of the ice dynamics, physical ice properties, boundary conditions, and geometry. In the present study we use scales for the bed elevation, b, the slope of the retrograde bed, s, the surface mass balance, a, and the bed friction, C, obtained from observational and model data (for details see Sect. 2.2).
The procedure to infer these scales from the data is schematized in Fig. 1: for each of the tributaries considered in this study a transect is defined that represents a center line of the ice stream and covers its potentially unstable bed section close to the grounding line. Since this study aims at providing a scaling analysis, the transects were not chosen following a strict definition that involves the velocity or topography fields. They were chosen to be straight lines that allow the quantification of a generic slope of the topography. The results presented here do not depend on the precise choice of the position of these transects. Fitting a linear slope to the retrograde bed section (blue line), the bed elevation b at the starting point of the slope and the slope magnitude s serve as characteristic geometric scales for the sloping bed on which the ice sheet is grounded. Thus, b is a representative scale also for the thickness of the ice below sea level in the vicinity of the grounding line. Basal friction C is averaged along this section to represent local conditions, and the surface mass balance a is obtained from averaging over the catchment that feeds the ice stream (Fig. 2 and Figs. S1–S9 in the Supplement). For each tributary these physical parameters are taken relative to the reference values of PIG (primed vs. unprimed parameters). The resulting scaling ratios are then used to calculate timescale ratios via two independent scaling conditions coming out of the similitude principle. We assume that the inferred timescales correspond to the outlet-specific initial response time to potential destabilization. We choose PIG as the reference, as it is one of the most prominent tributaries of West Antarctica and it is relatively well observed. Due to the nature of the conducted scaling analysis the scales calculated here could also be expressed relative to any other of the examined outlets without changing the results.
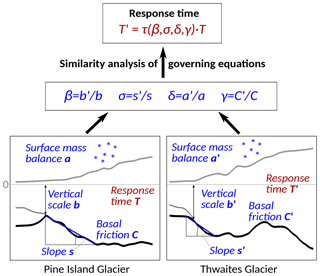
Figure 1Schematic visualizing the presented approach to obtain the response-time ratio τ between different Antarctic outlets as a function of their specific physical properties, here exemplified for Pine Island Glacier (unprimed reference) and Thwaites Glacier (primed scales). Blue variables are obtained from observations and model data. The equations for τ (Eqs. 2 and 3) result from a similarity analysis of the stress balance and conservation of mass (Feldmann and Levermann, 2016).
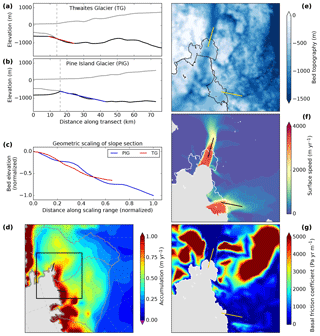
Figure 2Scaling of bed geometry and maps of data involved in the response-time calculation (here shown exemplarily for Thwaites Glacier – TG – with respect to the reference Pine Island Glacier – PIG). (a)–(b) Elevation of ice surface (grey) and bedrock (black) with retrograde slope section (colored) that is used to infer the vertical scale and the slope magnitude for the transects shown in panels (d)–(g). Panel (c) shows the bed geometry of the retrograde slope section, scaled with vertical and horizontal scaling factors (Table 1) and normalized to the dimensions of Pine Island Glacier. Maps of (d) surface mass balance (van Wessem et al., 2014), (e) bed topography (Fretwell et al., 2013), (f) surface velocity (Rignot et al., 2011) and (g) basal friction (Morlighem et al., 2013). Drainage basins are obtained from Zwally et al. (2012). The transects as shown in panels (a) and (b) are provided as black and yellow lines in panels (d)–(g).
2.1 Scaling laws and uncertainty criteria
The first of the two scaling laws used in this study is derived from the isothermal, two-dimensional SSA (Feldmann and Levermann, 2016, Eq. 1). More precisely, the scaling condition comes out of the non-dimensionalized frictional term of the SSA (see Eqs. 9 and 11 in Feldmann and Levermann, 2016). In its general form, it reads
being a function of the slope scaling ratio , the vertical scaling factor and the scaling ratio of basal friction . The friction exponent m stems from the Weertman-type sliding law that enters the SSA (see Eq. 3 in Feldmann and Levermann, 2016). The friction data applied in this study are obtained from an inversion model that assumes a linear relation between basal friction and ice velocity (m=1) with a spatially varying proportionality constant C (Morlighem et al., 2013). For this linear case, Eq. (1) simplifies to
As a consequence, for example, more slippery bed conditions (lower γ) and a steeper bed slope (higher σ) yield a shorter timescale (smaller response time).
The second scaling law () used here results from mass conservation (Feldmann and Levermann, 2016, Eqs. 4 and 13). It is independent of basal properties but a function of the vertical scaling β and the surface-mass-balance ratio , i.e.,
According to Eq. (3), an initially stable situation with stronger accumulation but initially thinner ice at the grounding line, for example, results in a faster response in the case of destabilization. As detailed in Feldmann and Levermann (2016), the above scaling laws (Eqs. 2 and 3) are consistent with analytic solutions of the ice-dynamic equations (Schoof, 2007).
Calculation of the time-scaling ratios τ and provides two independent estimates for the response time of each outlet examined here, values which are relative to the reference PIG. We use the deviation between the two values as a measure for the uncertainty of the estimation, accounting for observational uncertainty and approximations in our approach. In order to consider the calculated response-time scaling of a tributary with sufficient certainty we require the two calculated response-time ratios to fulfill the following conditions:
The first criterion compares the obtained qualitative scaling behavior which would be contradictory for c1<0 (one time-scaling ratio would indicate a faster response and the other a slower response compared to the reference). The second criterion yields the relative error between the two calculated response-time ratios with respect to their mean and ensures that this uncertainty is at most 20 %. Ice streams with a larger uncertainty in their calculated time scaling are reported in the following but considered to be unsuitable for the approach used here.
2.2 Data
The locations of the chosen transects are motivated by the bed topography and the flow field of the analyzed outlets to capture their retrograde bed section directly upstream of the grounding line (e.g., see Fig. 2). The ice-stream characteristic parameter values are all obtained from datasets that represent present-day conditions of the Antarctic Ice Sheet. The bed topography stems from the BEDMAP2 dataset (Fretwell et al., 2013), which is the most recent continent-wide compilation of Antarctic ice thickness and basal topography and involves data from various sources, including satellite, airborne radar, over-snow radar and seismic-sounding measurements that total to 25 million data points. The basal-friction dataset is taken from Morlighem et al. (2013) and is a product from inversion of observed present-day Antarctic ice-surface velocity (Rignot et al., 2011) with the Ice Sheet System Model (Larour et al., 2012). The thermo-mechanical, higher-order model uses anisotropic mesh refinement that allows for horizontal resolutions down to 3 km along the Antarctic coast, i.e., our region of interest. The field of basal friction is consistent with results from other inversion models (Joughin et al., 2009; Morlighem et al., 2010; Pollard and DeConto, 2012). Surface mass balance is obtained from the Regional Atmospheric Climate Model (RACMO version 2.3p2; van Wessem et al., 2014) and is averaged over the period from 1979 to 2016. RACMO is forced by ERA-Interim reanalysis data at the lateral boundaries, simulating the interaction of the ice sheet with its atmospheric environment, involving relevant processes such as solid precipitation, snow sublimation and surface meltwater runoff. For most of the tributaries the surface mass balance a is obtained from averaging over the entire feeding catchment basin (Zwally et al., 2012). For some basins that have a long coastline and are drained by several major tributaries the averaging area is constrained to a region upstream of the ice stream of interest (Figs. S3–S6 and S9).
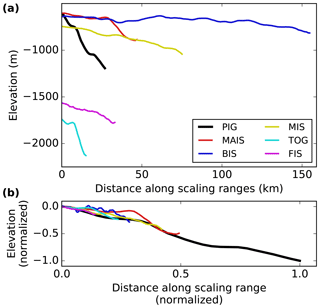
The examined individual retrograde bed slopes vary in magnitude by a factor of six and bed elevation differs by up to 1000 m (Figs. 3a and A2a). The lengths of the slope sections indicate how far the considered retrograde slopes reach inland before an (intermediate) section with vanishing slope or an upsloping bed follows (Figs. 2 and S1–S9). We scale these bed sections with respect to the reference according to the obtained vertical and horizontal length–scale ratios (Table 1). The resulting bed profiles collapse towards the reference showing similar downsloping while still exhibiting their characteristic pattern (Figs. 3b and A2b). This confirms that the chosen geometric measures adequately reflect the characteristics of the retrograde bed slopes.
Table 1Scaling ratios for all examined Antarctic outlets, clockwise, starting with the reference Pine Island Glacier. The ratios for the vertical scale (β), the retrograde-slope magnitude (σ), the basal friction (γ) and the surface mass balance friction (δ) are inferred from observational and model data (see Methods). The horizontal scaling ratio α, used for the scaling of the retrograde bed topography (Figs. 3 and A2), is calculated via . The scaling of the ice softness ζ is obtained from Eq. (A2). The response-time ratios τ and are calculated according to the scaling laws given by Eqs. (2) and (3). The last two columns show the resulting values from application of the two quality criteria (Eqs. 4 and 5) according to which tributaries are either accepted (bold) or discarded.
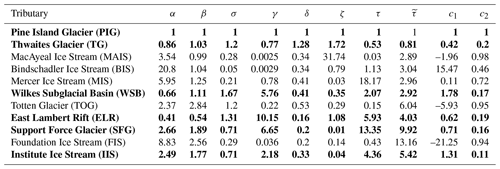
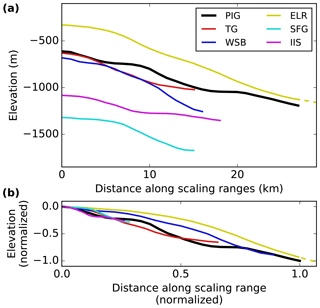
Figure 3(a) Unscaled bed topography of retrograde slope sections of the six examined Antarctic outlets that fulfill the time-scaling criteria. (b) Bed topography from panel (a) scaled according to similitude theory using the horizontal and vertical length–scale ratios obtained from observations (see Table 1) and normalized to the dimensions of the PIG slope (that has the same aspect ratio in both panels). For better visibility the x and y axis are cut (see Fig. S4 for full extent of the ELR bed section).
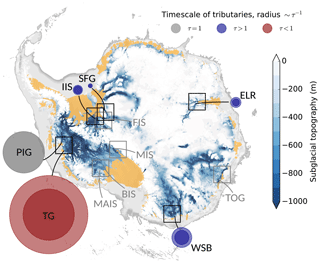
Figure 4Map of inverse response time of Antarctic tributaries (two circles for each, corresponding to the two independent estimates, τ and ; see Table 1) relative to Pine Island Glacier (grey circle) as obtained from similitude analysis. Rectangles denote examined regions as displayed in (Figs. 2 and S1–S9). Regions discarded from the analysis are shown in grey. Shown are (clockwise) Pine Island Glacier (PIG), Thwaites Glacier (TG), MacAyeal Ice Stream (MAIS), Bindschadler Ice Stream (BIS), Mercer Ice Stream (MIS), Wilkes Subglacial Basin (WSB), Totten Glacier (TOG), East Lambert Rift (ELR), Support Force Glacier (SFG), Foundation Ice Stream (FIS) and Institute Ice Stream (IIS). Marine bed topography in blue (color bar), ice shelves in yellow and continental shelf in grey are taken from BEDMAP2 (Fretwell et al., 2013).
Within the ensemble of analyzed outlets TG has the smallest response time (Fig. 4), being 1.25 to almost 2 times as fast as PIG, which is found to be the second fastest. For the chosen outlet of WSB the two calculated ratios indicate a response that would be twice as slow as PIG. East Lambert Rift (ELR) and Institute Ice Stream (IIS) that feed Amery Ice Shelf and Filchner-Ronne Ice Shelf, respectively, are found to be 4 to 6 times slower than PIG. By far the slowest response is shown by Support Force Glacier (SFG), which is (more than) 10 times slower than PIG.
For each of these six tributaries (Table 1, bold) both imposed quality criteria (Eqs. 4 and 5) are fulfilled with a maximum error of c2=20 %. The other five regions are discarded, since one or both of the criteria are not met, with c2 ranging from 46 % to 98 % (Table 1). Each of the discarded ice streams exhibits extremely slippery bed conditions, with basal-friction values of up to 3 orders of magnitude smaller than the reference (Table 1). On the other hand these outlets also have the smallest bed slopes of the ensemble. Both slope and friction are hence subject to large relative uncertainties that mutually amplify in the calculation of τ and hence amplify the mismatch with .
Throughout the successfully examined outlets, diagnosed basal friction and surface accumulation each differ by 1 order of magnitude. Most slippery conditions and the highest snowfall are found in the Amundsen Sea sector, both favoring the short timescales of PIG and TG. We also infer the scaling of the ice softness A using a third scaling law coming out of the similarity analysis from Feldmann and Levermann (2016) (see Appendix A). The resulting ratios differ by two orders of magnitude. For most of the ice streams discussed here a lower softness value corresponds to a larger timescale. In other words, stiffer ice tends to slow down the response to destabilization.
According to observations, PIG and TG have been showing the largest ice discharge rates in the Amundsen Sea Sector of West Antarctica since the last 4 decades, including phases of rapid ice speed-up, dynamic thinning and grounding-line retreat (Rignot et al., 2014; Mouginot et al., 2014; Konrad et al., 2018). PIG's most recent acceleration was found to coincide with the ungrounding of a region of only lightly grounded ice, and the grounding line that is now at the upstream end of this area has been stabilizing during the last few years (Mouginot et al., 2014). Meanwhile PIG's deceleration in ice discharge is more than compensated by TG's speed-up, which can be attributed to reduced ice-shelf buttressing that previously stabilized the upstream grounded ice (Rignot et al., 2014). It thus remains an open question whether the current destabilization of TG will result in retreat rates larger than PIG's recent retreat rates and hence confirm our finding of a faster timescale of TG compared to PIG. Regional model simulations of these regions (Favier et al., 2014; Joughin et al., 2014) indicate that TG's discharge rate is up to a factor of 2 larger than PIG's after the basal-melt perturbation has ceased and the glaciers have relaxed into a configuration of constant ice discharge.
The relatively large timescales of SFG, IIS and ELR, calculated here, are consistent with results from dynamical modeling that find these outlets of the Filchner-Ronne Ice Shelf and Amery Ice Shelf to be far less sensitive to instability (Gong et al., 2014; Wright et al., 2014; Thoma et al., 2015; Ritz et al., 2015; Mengel et al., 2016) than WSB (Mengel and Levermann, 2014) and PIG and TG (Favier et al., 2014; Joughin et al., 2014; Feldmann and Levermann, 2015; Seroussi et al., 2017). In these cases the buttressing effect of the large ice shelves and the narrow, channel-type bed topography confining these outlets as well as relatively high basal friction (Table 1) might prevent MISI initiation and limit grounding-line retreat.
Our results are obtained from the application of scaling laws, a procedure commonly pursued in hydrodynamics and engineering (e.g., Scruton, 1961; Li et al., 2013) and also to some extent in the field of glaciology (e.g., Burton et al., 2012; Corti et al., 2014). The two scaling laws used here (Eqs. 2 and 3) are derived from an approximation of the Stokes stress balance (Feldmann and Levermann, 2016). The approximation accounts for the dynamics of shallow ice streams that are characterized by dominating longitudinal stresses and rapid sliding and typically have an onset at a few 10 to 100 km upstream of the grounding line. Our analysis focuses precisely on such regions. The examined sections are all situated in the proximity of the grounding line and indeed exhibit slippery bed conditions and fast ice flow as indicated by inferred basal friction and velocity data, respectively (Figs. 2, S1–S9f and g).
The proposed method is based on the assumption that the ice-stream-specific properties can each be represented by a single scale. This is realized by averaging spatially varying, complex fields along a representative transect (ice softness and basal friction) or over the entire catchment basin (surface mass balance). While such an approach means a substantial idealization of the complex nature of ice dynamics, it allows for a timescale analysis that is based on representative ice-property scales and considers the relevant physics through the (simplified) stress balance. Our analysis will only be valid as long as this representation is sufficient. We chose 11 outlet glaciers around Antarctica that we deem suitable for our pragmatic method of collecting the required data along representative transects. Indeed, several more potentially MISI-prone Antarctic outlets exist, generally characterized by a curved shape. Their analysis would require a more sophisticated way of obtaining the data, e.g., along streamlines instead of straight lines, which is not considered in this study.
Our approach assumes idealized conditions of unstable retreat. Though taking into account bed friction as a possible stabilizing factor (Ritz et al., 2015) it is strongly limited by not explicitly accounting for the stabilizing effect of ice-shelf buttressing (Dupont and Alley, 2005; Gudmundsson, 2013). That is, the approach estimates the timescale of retreat only after no significant ice shelf is present anymore or for the situation of an unconfined ice shelf that does not provide any backstress (e.g., as might be the case for the present-day TG ice shelf; Rignot et al., 2014). Furthermore, our investigation is constrained to the short initial time period (decades to centuries) after destabilization, during which the grounding line passes the investigated retrograde bed-slope section near the coast.
The used datasets of observed bed and ice geometry still show substantial gaps in coverage, though the regions analyzed here lie at the lower end of the uncertainty range (Fretwell et al., 2013, their Figs. 11 and 12). Measurements of the Antarctic surface mass balance are in general sparsely distributed over the continent. In contrast, results from numerical modeling are known to have biases with respect to observations. To reduce uncertainty we use a surface-mass-balance dataset obtained from a regional climate model that was calibrated by the available observational data (van de Berg et al., 2006; van Wessem et al., 2014).
Combining observations and modeling data with a similarity analysis of the governing, simplified ice-dynamic equations we apply the similitude principle (Fig. 1) to 11 MISI-prone Antarctic outlets to infer their relative timescales (Fig. 4). Assuming potential destabilization of these outlets (MISI triggered) in the absence of ice-shelf buttressing, our results suggest that PIG and TG have the smallest response time to destabilization (Fig. 4; Table 1), with TG responding between 1.25 to almost 2 times as fast as PIG. Further considered ice streams draining East or West Antarctica are found to respond twice (WSB) to 10 times (SFG) as slow as PIG. This also suggests that the dynamic regime of PIG is more similar to TG than to any other of the outlets analyzed here. This way, the proposed scaling approach may help field workers in their decision on which glaciers to observe to be able to study a broad and thus insightful spectrum of different (dissimilar) glacier dynamics.
The presented analysis cannot make any statements about absolute timescales of the instabilities. It is constrained to relative statements between the different outlet glaciers based on their specific geometry and physical conditions, which carry information of the specific dynamic balance within the respective outlet glacier. Regarding absolute response times of individual tributaries, continued observation of the retreat of PIG and TG that extends the data that are already available might allow deducing long-term trends, thus giving estimates for the absolute timescales of instability. These could be used to calibrate the method presented here. Our method comes with a large number of assumptions and limitations. Uncertainties will reduce as observational data further improve, and the relevance of the results will increase with sophistication of the method (e.g., explicit inclusion of ice-shelf buttressing).
The datasets related to this paper are available upon request from the authors.
There is a third independent scaling law derived by similarity analysis in Feldmann and Levermann (2016), coming out of the viscous term of the SSA (see their Eqs. 9 and 12). Making the common choice of Glen's flow-law exponent n=3 (Greve and Blatter, 2009), it reads
involving the ice-softness ratio . Due the absence of Antarctic ice-softness data, we cannot utilize this scaling law to calculate a third independent timescale ratio. However, combining this third scaling law (Eq. A1) with the first one (Eq. 2), we eliminate the timescale ratio to calculate the ice-softness ratio via
Being dependent on the scaling of the geometry and the basal friction, ζ can be considered to be the ratio between ice-softness scales that are representative of the analyzed outlets cross sections (Table 1).
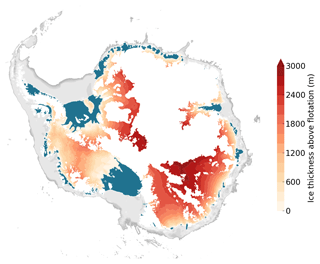
Figure A1Ice thickness above flotation of marine regions (bedrock below sea level) that are connected to the ocean (color bar). Ice shelves are in blue, and the continental shelf is in grey. Ice and bed topography are taken from the BEDMAP2 compilation (Fretwell et al., 2013).
The supplement related to this article is available online at: https://doi.org/10.5194/tc-13-1621-2019-supplement.
AL designed the study. AL and JF carried out the analysis and wrote the manuscript. JF prepared the figures.
The authors declare that they have no conflict of interest.
We thank Mathieu Morlighem for providing the dataset of Antarctic basal friction. We are grateful to J. Melchior van Wessem for providing the field of Antarctic surface mass balance. We thank Martin Lüthi and one anonymous reviewer for their valuable and helpful comments and suggestions.
This work was supported by the Deutsche
Forschungsgemeinschaft (DFG) in the framework of the priority
program “Antarctic Research with comparative investigations in
Arctic ice areas” by grant LE 1448/8-1.
The publication of this article was funded by the
Open Access Fund of the Leibniz Association.
This paper was edited by Kenichi Matsuoka and reviewed by Martin Lüthi and one anonymous referee.
Asay-Davis, X. S., Cornford, S. L., Durand, G., Galton-Fenzi, B. K., Gladstone, R. M., Gudmundsson, G. H., Hattermann, T., Holland, D. M., Holland, D., Holland, P. R., Martin, D. F., Mathiot, P., Pattyn, F., and Seroussi, H.: Experimental design for three interrelated marine ice sheet and ocean model intercomparison projects: MISMIP v. 3 (MISMIP +), ISOMIP v. 2 (ISOMIP +) and MISOMIP v. 1 (MISOMIP1), Geosci. Model Dev., 9, 2471–2497, https://doi.org/10.5194/gmd-9-2471-2016, 2016. a
Bamber, J. L., Riva, R. E. M., Vermeersen, B. L. A., and LeBrocq, A. M.: Reassessment of the Potential Sea-Level Rise from a Collapse of the West Antarctic Ice Sheet, Science, 324, 901–903, https://doi.org/10.1126/science.1169335, 2009. a
Bentley, C. R., Crary, A. P., Ostenso, N. A., and Thiel, E. C.: Structure of West Antarctica, Science, 131, 131–136, https://doi.org/10.1126/science.131.3394.131, 1960. a
Buckingham, E.: On Physically Similar Systems; Illustrations of the Use of Dimensional Equations, Phys. Rev., 4, 345–376, https://doi.org/10.1103/PhysRev.4.345, 1914. a
Burton, J. C., Amundson, J. M., Abbot, D. S., Boghosian, A., Cathles, L. M., Correa-Legisos, S., Darnell, K. N., Guttenberg, N., Holland, D. M., and MacAyeal, D. R.: Laboratory Investigations of Iceberg Capsize Dynamics, Energy Dissipation and Tsunamigenesis: Iceberg capsize dynamics, J. Geophys. Res.-Earth, 117, F01007, https://doi.org/10.1029/2011JF002055, 2012. a
Cook, S. J. and Swift, D. A.: Subglacial Basins: Their Origin and Importance in Glacial Systems and Landscapes, Earth-Sci. Rev., 115, 332–372, https://doi.org/10.1016/j.earscirev.2012.09.009, 2012. a
Corti, G., Zeoli, A., and Iandelli, I.: Small-Scale Modeling of Ice Flow Perturbations Induced by Sudden Ice Shelf Breakup, Global Planet. Change, 119, 51–55, https://doi.org/10.1016/j.gloplacha.2014.05.002, 2014. a
DeConto, R. M. and Pollard, D.: Contribution of Antarctica to Past and Future Sea-Level Rise, Nature, 531, 591–597, https://doi.org/10.1038/nature17145, 2016. a
Dupont, T. K. and Alley, R. B.: Assessment of the Importance of Ice-Shelf Buttressing to Ice-Sheet Flow: buttressing sensitivity, Geophys. Res. Lett., 32, L04503, https://doi.org/10.1029/2004GL022024, 2005. a, b, c
Favier, L., Gagliardini, O., Durand, G., and Zwinger, T.: A three-dimensional full Stokes model of the grounding line dynamics: effect of a pinning point beneath the ice shelf, The Cryosphere, 6, 101–112, https://doi.org/10.5194/tc-6-101-2012, 2012. a
Favier, L., Durand, G., Cornford, S. L., Gudmundsson, G. H., Gagliardini, O., Gillet-Chaulet, F., Zwinger, T., Payne, A. J., and Le Brocq, A. M.: Retreat of Pine Island Glacier Controlled by Marine Ice-Sheet Instability, Nat. Clim. Change, 4, 117–121, https://doi.org/10.1038/nclimate2094, 2014. a, b, c
Feldmann, J. and Levermann, A.: Collapse of the West Antarctic Ice Sheet after Local Destabilization of the Amundsen Basin, P. Natl. Acad. Sci. USA, 112, 14191–14196, https://doi.org/10.1073/pnas.1512482112, 2015. a, b
Feldmann, J. and Levermann, A.: Similitude of ice dynamics against scaling of geometry and physical parameters, The Cryosphere, 10, 1753–1769, https://doi.org/10.5194/tc-10-1753-2016, 2016. a, b, c, d, e, f, g, h, i, j, k
Fretwell, P., Pritchard, H. D., Vaughan, D. G., Bamber, J. L., Barrand, N. E., Bell, R., Bianchi, C., Bingham, R. G., Blankenship, D. D., Casassa, G., Catania, G., Callens, D., Conway, H., Cook, A. J., Corr, H. F. J., Damaske, D., Damm, V., Ferraccioli, F., Forsberg, R., Fujita, S., Gim, Y., Gogineni, P., Griggs, J. A., Hindmarsh, R. C. A., Holmlund, P., Holt, J. W., Jacobel, R. W., Jenkins, A., Jokat, W., Jordan, T., King, E. C., Kohler, J., Krabill, W., Riger-Kusk, M., Langley, K. A., Leitchenkov, G., Leuschen, C., Luyendyk, B. P., Matsuoka, K., Mouginot, J., Nitsche, F. O., Nogi, Y., Nost, O. A., Popov, S. V., Rignot, E., Rippin, D. M., Rivera, A., Roberts, J., Ross, N., Siegert, M. J., Smith, A. M., Steinhage, D., Studinger, M., Sun, B., Tinto, B. K., Welch, B. C., Wilson, D., Young, D. A., Xiangbin, C., and Zirizzotti, A.: Bedmap2: improved ice bed, surface and thickness datasets for Antarctica, The Cryosphere, 7, 375–393, https://doi.org/10.5194/tc-7-375-2013, 2013. a, b, c, d, e, f
Goldberg, D., Holland, D. M., and Schoof, C.: Grounding Line Movement and Ice Shelf Buttressing in Marine Ice Sheets, J. Geophys. Res., 114, F04026, https://doi.org/10.1029/2008JF001227, 2009. a, b
Golledge, N. R., Kowalewski, D. E., Naish, T. R., Levy, R. H., Fogwill, C. J., and Gasson, E. G. W.: The Multi-Millennial Antarctic Commitment to Future Sea-Level Rise, Nature, 526, 421–425, https://doi.org/10.1038/nature15706, 2015. a
Gong, Y., Cornford, S. L., and Payne, A. J.: Modelling the response of the Lambert Glacier–Amery Ice Shelf system, East Antarctica, to uncertain climate forcing over the 21st and 22nd centuries, The Cryosphere, 8, 1057–1068, https://doi.org/10.5194/tc-8-1057-2014, 2014. a
Greenbaum, J. S., Blankenship, D. D., Young, D. A., Richter, T. G., Roberts, J. L., Aitken, A. R. A., Legresy, B., Schroeder, D. M., Warner, R. C., van Ommen, T. D., and Siegert, M. J.: Ocean Access to a Cavity beneath Totten Glacier in East Antarctica, Nat. Geosci., 8, 294–298, https://doi.org/10.1038/ngeo2388, 2015. a
Greene, C. A., Blankenship, D. D., Gwyther, D. E., Silvano, A., and van Wijk, E.: Wind Causes Totten Ice Shelf Melt and Acceleration, Science Advances, 3, e1701681, https://doi.org/10.1126/sciadv.1701681, 2017. a
Greve, R. and Blatter, H.: Dynamics of Ice Sheets and Glaciers, Advances in Geophysical and Environmental Mechanics and Mathematics, Springer Berlin Heidelberg, Berlin, Heidelberg, https://doi.org/10.1007/978-3-642-03415-2, 2009. a, b
Gudmundsson, G. H.: Ice-shelf buttressing and the stability of marine ice sheets, The Cryosphere, 7, 647–655, https://doi.org/10.5194/tc-7-647-2013, 2013. a
Gudmundsson, G. H., Krug, J., Durand, G., Favier, L., and Gagliardini, O.: The stability of grounding lines on retrograde slopes, The Cryosphere, 6, 1497–1505, https://doi.org/10.5194/tc-6-1497-2012, 2012. a, b
Hellmer, H. H., Kauker, F., Timmermann, R., Determann, J., and Rae, J.: Twenty-First-Century Warming of a Large Antarctic Ice-Shelf Cavity by a Redirected Coastal Current, Nature, 485, 225–228, https://doi.org/10.1038/nature11064, 2012. a
Hillenbrand, C.-D., Smith, J. A., Hodell, D. A., Greaves, M., Poole, C. R., Kender, S., Williams, M., Andersen, T. J., Jernas, P. E., Elderfield, H., Klages, J. P., Roberts, S. J., Gohl, K., Larter, R. D., and Kuhn, G.: West Antarctic Ice Sheet Retreat Driven by Holocene Warm Water Incursions, Nature, 547, 43–48, https://doi.org/10.1038/nature22995, 2017. a
Huybrechts, P., Goelzer, H., Janssens, I., Driesschaert, E., Fichefet, T., Goosse, H., and Loutre, M.-F.: Response of the Greenland and Antarctic Ice Sheets to Multi-Millennial Greenhouse Warming in the Earth System Model of Intermediate Complexity LOVECLIM, Surv. Geophys., 32, 397–416, https://doi.org/10.1007/s10712-011-9131-5, 2011. a
The IMBIE team: Mass Balance of the Antarctic Ice Sheet from 1992 to 2017, Nature, 558, 219–222, https://doi.org/10.1038/s41586-018-0179-y, 2018. a
IPCC, WG I: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013. a
IPCC, WG II: Climate Change 2014: Impacts, Adaptation, and Vulnerability, Part A: Global and Sectoral Aspects, Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Field, C. B., Barros, V. R., Dokken, D. J., Mach, K. J., Mastrandrea, M. D., Bilir, T. E., Chatterjee, M., Ebi, K. L., Estrada, Y. O., Genova, R. C., Girma, B., Kissel, E. S., Levy, A. N., MacCracken, S., Mastrandrea, P. R., and White, L. L., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2014. a
Jenkins, A., Dutrieux, P., Jacobs, S. S., McPhail, S. D., Perrett, J. R., Webb, A. T., and White, D.: Observations beneath Pine Island Glacier in West Antarctica and Implications for Its Retreat, Nat. Geosci., 3, 468–472, https://doi.org/10.1038/ngeo890, 2010. a
Jenkins, A., Shoosmith, D., Dutrieux, P., Jacobs, S., Kim, T. W., Lee, S. H., Ha, H. K., and Stammerjohn, S.: West Antarctic Ice Sheet Retreat in the Amundsen Sea Driven by Decadal Oceanic Variability, Nat. Geosci., 11, 733–738, https://doi.org/10.1038/s41561-018-0207-4, 2018. a
Joughin, I. and Alley, R. B.: Stability of the West Antarctic Ice Sheet in a Warming World, Nat. Geosci., 4, 506–513, https://doi.org/10.1038/ngeo1194, 2011. a
Joughin, I., Tulaczyk, S., Bamber, J. L., Blankenship, D., Holt, J. W., Scambos, T., and Vaughan, D. G.: Basal Conditions for Pine Island and Thwaites Glaciers, West Antarctica, Determined Using Satellite and Airborne Data, J. Glaciol., 55, 245–257, https://doi.org/10.3189/002214309788608705, 2009. a, b
Joughin, I., Smith, B. E., and Medley, B.: Marine Ice Sheet Collapse Potentially Under Way for the Thwaites Glacier Basin, West Antarctica, Science, 344, 735–738, https://doi.org/10.1126/science.1249055, 2014. a, b, c
Konrad, H., Shepherd, A., Gilbert, L., Hogg, A. E., McMillan, M., Muir, A., and Slater, T.: Net Retreat of Antarctic Glacier Grounding Lines, Nat. Geosci., 11, 258–262, https://doi.org/10.1038/s41561-018-0082-z, 2018. a, b
Kundu, P., Cohen, I., and Hu, H.: Fluid Mechanics, Academic Press, New Delhi, 2012. a
Larour, E., Seroussi, H., Morlighem, M., and Rignot, E.: Continental Scale, High Order, High Spatial Resolution, Ice Sheet Modeling Using the Ice Sheet System Model (ISSM): ice sheet system model, J. Geophys. Res.-Earth, 117, F01022, https://doi.org/10.1029/2011JF002140, 2012. a
Li, Y., Wu, M., Chen, X., Wang, T., and Liao, H.: Wind-Tunnel Study of Wake Galloping of Parallel Cables on Cable-Stayed Bridges and Its Suppression, Wind Struct., 16, 249–261, https://doi.org/10.12989/was.2013.16.3.249, 2013. a
Macagno, E. O.: Historico-Critical Review of Dimensional Analysis, J. Franklin I., 292, 391–402, https://doi.org/10.1016/0016-0032(71)90160-8, 1971. a
MacAyeal, D. R.: Large-Scale Ice Flow over a Viscous Basal Sediment: Theory and Application to Ice Stream B, Antarctica, J. Geophys. Res.-Sol. Ea., 94, 4071–4087, https://doi.org/10.1029/JB094iB04p04071, 1989. a
Medley, B., Joughin, I., Smith, B. E., Das, S. B., Steig, E. J., Conway, H., Gogineni, S., Lewis, C., Criscitiello, A. S., McConnell, J. R., van den Broeke, M. R., Lenaerts, J. T. M., Bromwich, D. H., Nicolas, J. P., and Leuschen, C.: Constraining the recent mass balance of Pine Island and Thwaites glaciers, West Antarctica, with airborne observations of snow accumulation, The Cryosphere, 8, 1375–1392, https://doi.org/10.5194/tc-8-1375-2014, 2014. a
Mengel, M. and Levermann, A.: Ice Plug Prevents Irreversible Discharge from East Antarctica, Nat. Clim. Change, 4, 451–455, https://doi.org/10.1038/nclimate2226, 2014. a, b
Mengel, M., Feldmann, J., and Levermann, A.: Linear Sea-Level Response to Abrupt Ocean Warming of Major West Antarctic Ice Basin, Nat. Clim. Change, 6, 71–74, https://doi.org/10.1038/nclimate2808, 2016. a, b
Mercer, J. H.: West Antarctic Ice Sheet and CO2 Greenhouse Effect: A Threat of Disaster, Nature, 271, 321–325, https://doi.org/10.1038/271321a0, 1978. a
Morland, L. W.: Unconfined Ice-Shelf Flow, in: Dynamics of the West Antarctic Ice Sheet, edited by: Van der Veen, C. J. and Oerlemans, J., Glaciology and Quaternary Geology, Springer Netherlands, 99–116, 1987. a
Morlighem, M., Rignot, E., Seroussi, H., Larour, E., Ben Dhia, H., and Aubry, D.: Spatial Patterns of Basal Drag Inferred Using Control Methods from a Full-Stokes and Simpler Models for Pine Island Glacier, West Antarctica: spatial patterns of basal drag, Geophys. Res. Lett., 37, L14502, https://doi.org/10.1029/2010GL043853, 2010. a
Morlighem, M., Seroussi, H., Larour, E., and Rignot, E.: Inversion of Basal Friction in Antarctica Using Exact and Incomplete Adjoints of a Higher-Order Model: Antarctic basal friction inversion, J. Geophys. Res.-Earth, 118, 1746–1753, https://doi.org/10.1002/jgrf.20125, 2013. a, b, c
Mouginot, J., Rignot, E., and Scheuchl, B.: Sustained Increase in Ice Discharge from the Amundsen Sea Embayment, West Antarctica, from 1973 to 2013, Geophys. Res. Lett., 41, 1576–1584, https://doi.org/10.1002/2013GL059069, 2014. a, b, c
Paolo, F. S., Fricker, H. A., and Padman, L.: Volume Loss from Antarctic Ice Shelves Is Accelerating, Science, 348, 327–331, https://doi.org/10.1126/science.aaa0940, 2015. a
Pattyn, F.: The Paradigm Shift in Antarctic Ice Sheet Modelling, Nat. Commun., 9, 2728, https://doi.org/10.1038/s41467-018-05003-z, 2018. a
Pattyn, F., Ritz, C., Hanna, E., Asay-Davis, X., DeConto, R., Durand, G., Favier, L., Fettweis, X., Goelzer, H., Golledge, N. R., Munneke, P. K., Lenaerts, J. T. M., Nowicki, S., Payne, A. J., Robinson, A., Seroussi, H., Trusel, L. D., and van den Broeke, M.: The Greenland and Antarctic Ice Sheets under 1.5 ∘C Global Warming, Nat. Clim. Change, 8, 1053–1061, https://doi.org/10.1038/s41558-018-0305-8, 2018. a
Pollard, D. and DeConto, R. M.: A simple inverse method for the distribution of basal sliding coefficients under ice sheets, applied to Antarctica, The Cryosphere, 6, 953–971, https://doi.org/10.5194/tc-6-953-2012, 2012. a
Pritchard, H. D., Ligtenberg, S. R. M., Fricker, H. A., Vaughan, D. G., van den Broeke, M. R., and Padman, L.: Antarctic Ice-Sheet Loss Driven by Basal Melting of Ice Shelves, Nature, 484, 502–505, https://doi.org/10.1038/nature10968, 2012. a
Rayleigh: The Principle of Similitude, Nature, 95, 66–68, https://doi.org/10.1038/095066c0, 1915. a
Reynolds, O.: An Experimental Investigation of the Circumstances Which Determine Whether the Motion of Water Shall Be Direct or Sinuous, and of the Law of Resistance in Parallel Channels, Philos. T. R. Soc. Lond., 174, 935–982, https://doi.org/10.1098/rstl.1883.0029, 1883. a, b
Rignot, E., Mouginot, J., and Scheuchl, B.: Ice Flow of the Antarctic Ice Sheet, Science, 333, 1427–1430, https://doi.org/10.1126/science.1208336, 2011. a, b
Rignot, E., Mouginot, J., Morlighem, M., Seroussi, H., and Scheuchl, B.: Widespread, Rapid Grounding Line Retreat of Pine Island, Thwaites, Smith, and Kohler Glaciers, West Antarctica, from 1992 to 2011, Geophys. Res. Lett., 41, 3502–3509, https://doi.org/10.1002/2014GL060140, 2014. a, b, c, d
Ritz, C., Edwards, T. L., Durand, G., Payne, A. J., Peyaud, V., and Hindmarsh, R. C. A.: Potential Sea-Level Rise from Antarctic Ice-Sheet Instability Constrained by Observations, Nature, 528, 115–118, https://doi.org/10.1038/nature16147, 2015. a, b, c
Ross, N., Bingham, R. G., Corr, H. F. J., Ferraccioli, F., Jordan, T. A., Le Brocq, A., Rippin, D. M., Young, D., Blankenship, D. D., and Siegert, M. J.: Steep Reverse Bed Slope at the Grounding Line of the Weddell Sea Sector in West Antarctica, Nat. Geosci., 5, 393–396, https://doi.org/10.1038/ngeo1468, 2012. a
Schoof, C.: Ice Sheet Grounding Line Dynamics: Steady States, Stability, and Hysteresis, J. Geophys. Res., 112, F03S28, https://doi.org/10.1029/2006JF000664, 2007. a, b
Scruton, C.: Wind Tunnels and Flow Visualization, Nature, 189, 108–110, https://doi.org/10.1038/189108a0, 1961. a
Seroussi, H., Nakayama, Y., Larour, E., Menemenlis, D., Morlighem, M., Rignot, E., and Khazendar, A.: Continued Retreat of Thwaites Glacier, West Antarctica, Controlled by Bed Topography and Ocean Circulation: Ice-ocean modeling of thwaites glacier, Geophys. Res. Lett., 44, 6191–6199, https://doi.org/10.1002/2017GL072910, 2017. a, b
Shean, D. E., Joughin, I. R., Dutrieux, P., Smith, B. E., and Berthier, E.: Ice shelf basal melt rates from a high-resolution DEM record for Pine Island Glacier, Antarctica, The Cryosphere Discuss., https://doi.org/10.5194/tc-2018-209, in review, 2018. a
Smith, J. A., Andersen, T. J., Shortt, M., Gaffney, A. M., Truffer, M., Stanton, T. P., Bindschadler, R., Dutrieux, P., Jenkins, A., Hillenbrand, C.-D., Ehrmann, W., Corr, H. F. J., Farley, N., Crowhurst, S., and Vaughan, D. G.: Sub-Ice-Shelf Sediments Record History of Twentieth-Century Retreat of Pine Island Glacier, Nature, 541, 77–80, https://doi.org/10.1038/nature20136, 2017. a
Szücs, E.: Fundamental Studies in Engineering II, Similitude and Modeling, Elsevier Scientific Publishing Co., Amsterdam, Netherlands, 1980. a
Thoma, M., Determann, J., Grosfeld, K., Goeller, S., and Hellmer, H. H.: Future Sea-Level Rise Due to Projected Ocean Warming beneath the Filchner Ronne Ice Shelf: A Coupled Model Study, Earth Planet. Sc. Lett., 431, 217–224, https://doi.org/10.1016/j.epsl.2015.09.013, 2015. a, b
Timmermann, R. and Hellmer, H. H.: Southern Ocean Warming and Increased Ice Shelf Basal Melting in the Twenty-First and Twenty-Second Centuries Based on Coupled Ice-Ocean Finite-Element Modelling, Ocean Dynam., 63, 1011–1026, https://doi.org/10.1007/s10236-013-0642-0, 2013. a
van de Berg, W. J., van den Broeke, M. R., Reijmer, C. H., and van Meijgaard, E.: Reassessment of the Antarctic Surface Mass Balance Using Calibrated Output of a Regional Atmospheric Climate Model, J. Geophys. Res., 111, D11104, https://doi.org/10.1029/2005JD006495, 2006. a
van Wessem, J. M., Reijmer, C. H., Lenaerts, J. T. M., van de Berg, W. J., van den Broeke, M. R., and van Meijgaard, E.: Updated cloud physics in a regional atmospheric climate model improves the modelled surface energy balance of Antarctica, The Cryosphere, 8, 125–135, https://doi.org/10.5194/tc-8-125-2014, 2014. a, b, c
Weertman, J.: Stability of the Junction of an Ice Sheet and an Ice Shelf, J. Glaciol., 13, 3–11, https://doi.org/10.3189/S0022143000023327, 1974. a
Winkelmann, R., Levermann, A., Ridgwell, A., and Caldeira, K.: Combustion of Available Fossil Fuel Resources Sufficient to Eliminate the Antarctic Ice Sheet, Science Advances, 1, e1500589, https://doi.org/10.1126/sciadv.1500589, 2015. a
Wright, A. P., Le Brocq, A. M., Cornford, S. L., Bingham, R. G., Corr, H. F. J., Ferraccioli, F., Jordan, T. A., Payne, A. J., Rippin, D. M., Ross, N., and Siegert, M. J.: Sensitivity of the Weddell Sea sector ice streams to sub-shelf melting and surface accumulation, The Cryosphere, 8, 2119–2134, https://doi.org/10.5194/tc-8-2119-2014, 2014. a, b
Zwally, H. J., Giovinetto, M. B., Beckley, M. A., and Saba, J. L.: Antarctic and Greenland Drainage Systems, GSFC Cryospheric Sciences Laboratory, available at: http://icesat4.gsfc.nasa.gov/cryo_data/ant_grn_drainage_systems.php (last access: 1 May 2018), 2012. a, b