the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Intercomparison and improvement of two-stream shortwave radiative transfer schemes in Earth system models for a unified treatment of cryospheric surfaces
Charles S. Zender
Mark G. Flanner
Snow is an important climate regulator because it greatly increases the surface albedo of middle and high latitudes of the Earth. Earth system models (ESMs) often adopt two-stream approximations with different radiative transfer techniques, the same snow therefore has different solar radiative properties depending whether it is on land or on sea ice. Here we intercompare three two-stream algorithms widely used in snow models, improve their predictions at large zenith angles, and introduce a hybrid model suitable for all cryospheric surfaces in ESMs. The algorithms are those employed by the SNow ICe and Aerosol Radiative (SNICAR) module used in land models, dEdd–AD used in Icepack, the column physics used in the Los Alamos sea ice model CICE and MPAS-Seaice, and a two-stream discrete-ordinate (2SD) model. Compared with a 16-stream benchmark model, the errors in snow visible albedo for a direct-incident beam from all three two-stream models are small () and increase as snow shallows, especially for aged snow. The errors in direct near-infrared (near-IR) albedo are small () for solar zenith angles θ<75∘, and increase as θ increases. For diffuse incidence under cloudy skies, dEdd–AD produces the most accurate snow albedo for both visible and near-IR () with the lowest underestimate (−0.01) for melting thin snow. SNICAR performs similarly to dEdd–AD for visible albedos, with a slightly larger underestimate (−0.02), while it overestimates the near-IR albedo by an order of magnitude more (up to 0.04). 2SD overestimates both visible and near-IR albedo by up to 0.03. We develop a new parameterization that adjusts the underestimated direct near-IR albedo and overestimated direct near-IR heating persistent across all two-stream models for θ>75∘. These results are incorporated in a hybrid model SNICAR-AD, which can now serve as a unified solar radiative transfer model for snow in ESM land, land ice, and sea ice components.
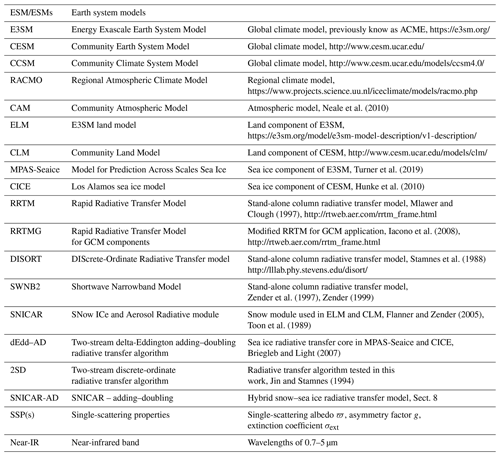
Snow cover on land, land ice, and sea ice, modulates the surface energy balance of middle and high latitudes of the Earth, principally because even a thin layer of snow can greatly increase the surface albedo. Integrated over the solar spectrum, the broadband albedo of opaque snow ranges from 0.7 to 0.9 (e.g., Wiscombe and Warren, 1980; Dang et al., 2015). In contrast, the albedo of other natural surfaces is smaller: 0.2, 0.25, and 0.5–0.7 for damp soil, grassland, and bare multi-year sea ice, respectively (Perovich, 1996; Liang et al., 2002; Brandt et al., 2005; Bøggild et al., 2010). The accumulation, evolution, and depletion of snow cover thus modify the seasonal cycle of surface albedo globally. In particular, snow over sea ice absorbs more solar energy and begins to melt in the spring, which forms melt ponds that bring the sea ice albedo to as low as 0.15 to further accelerate ice melt (Light et al., 2008, 2015). An accurate simulation of the shortwave radiative properties of snowpack is therefore crucial for spectrally partitioning solar energy and representing snow–albedo feedbacks across the Earth system. Unfortunately, computational demands and coupling architectures often constrain representation of snowpack radiative processes in Earth system models (ESMs; please refer to Table 1 for all abbreviations used in this work) to relatively crude approximations such as two-stream methods (Wiscombe and Warren, 1980; Toon et al., 1989). In this work, we intercompare two-stream methods widely used in snow models and then introduce a new parameterization that significantly reduces their snowpack reflectance and heating biases at large zenith angles, to produce more realistic behavior in polar regions.
Table 1Abbreviations used in this paper and their references. Last access date for all cited URLs in this table is 22 July 2019.
Snow albedo is determined by many factors including the snow grain radius, the solar zenith angle, cloud transmittance, light-absorbing particles, and the albedo of underlying ground if snow is optically thin (Wiscombe and Warren, 1980; Warren and Wiscombe, 1980); it also varies strongly with wavelength since the ice absorption coefficient varies by 7 orders of magnitudes across the solar spectrum (Warren and Brandt, 2008). At visible wavelengths (0.2–0.7 µm), ice is almost nonabsorptive such that the absorption of visible energy by snowpack is mostly due to the light-absorbing particles (e.g., black carbon, organic carbon, mineral dust) that were incorporated during ice nucleation in clouds, scavenged during precipitation, or slowly sedimented from the atmosphere by gravity (Warren and Wiscombe, 1980, 1985; Doherty et al., 2010, 2014, 2016; Wang et al., 2013; Dang and Hegg, 2014). As snow becomes shallower, visible photons are more likely to penetrate through snowpack and get absorbed by darker underlying ground. At near-infrared (near-IR) wavelengths (0.7–5 µm), ice is much more absorptive, so that the snow near-IR albedo is lower than the visible albedo. Larger ice crystals form a lower albedo surface than smaller ice crystals; hence aged snowpacks absorb more solar energy. Photons incident at smaller solar zenith angles are more likely to penetrate deeper vertically and be scattered in the snowpack until being absorbed by the ice, the underlying ground, or absorbing impurities, which also leads to a smaller snow albedo. To compute the reflected solar flux, spectrally resolved albedo must be weighted by the incident solar flux, which is mostly determined by solar zenith angle, cloud cover and transmittance, and column water vapor. Modeling the solar properties of snowpacks must consider the spectral signatures of these atmospheric properties.
Several parameterizations have been developed to compute the snow solar properties without solving the radiative transfer equations and some are incorporated into ESMs or regional models. Marshall and Warren (1987) and Marshall (1989) parameterized snow albedo in both visible and near-IR bands as functions of snow grain size, solar zenith angle, cloud transmittance, snow depth, underlying surface albedo, and black carbon content. Marshall and Oglesby (1994) used this in an ESM. Gardner and Sharp (2010) computed the all-wave snow albedo with similar inputs. This was incorporated into the regional climate model RACMO (https://www.projects.science.uu.nl/iceclimate/models/racmo.php, last access: 22 July 2019) to simulate snow albedo in glaciered regions like Antarctica and Greenland (Kuipers Munneke et al., 2011). Dang et al. (2015) parameterized snow albedo as a function of snow grain radius, black carbon content, and dust content for visible and near-IR bands and 14 narrower bands used in the Rapid Radiative Transfer Model (RRTM; Mlawer and Clough, 1997). Their algorithm can also be expanded to different solar zenith angles using the zenith angle parameterization developed by Marshall and Warren (1987). Aoki et al. (2011) developed a more complex model based on the offline snow albedo and a transmittance look-up table. This can be applied to multilayer snowpack to compute the snow albedo and the solar heating profiles as functions of snow grain size, black carbon and dust content, snow temperature, and snowmelt water equivalent. These parameterizations are often in the form of simplified polynomial equations, which are especially suitable to long-term ESM simulations that require less time-consuming snow representations.
More complex models that explicitly solve the multiple-scattering radiative transfer equations have also been developed to compute snow solar properties. Flanner and Zender (2005) developed the SNow Ice and Aerosol Radiation model (SNICAR) that utilizes two-stream approximations (Wiscombe and Warren, 1980; Toon et al., 1989) to predict heating and reflectance for a multilayer snowpack. They implemented SNICAR in the Community Land Model (CLM) to predict snow albedo and vertically resolved solar absorption for snow-covered surfaces. Before SNICAR, CLM prescribed snow albedo and confined all solar absorption to the top snow layer (Flanner and Zender, 2005). Over the past decades, updates and new features have been added to SNICAR to consider more processes such as black carbon–ice mixing states (Flanner et al., 2012) and snow grain shape (He et al., 2018b). Concurrent with the development of SNICAR, Briegleb and Light (2007) improved the treatment of sea ice solar radiative calculations in the Community Climate System Model (CCSM). They implemented a different two-stream scheme with delta-Eddington approximation and the adding–doubling technique (hereafter, dEdd–AD) that allows CCSM to compute bare, ponded, and snow-covered sea ice albedo and solar absorption profiles of multilayer sea ice. Before these improvements, the sea ice albedo was computed based on surface temperature, snow thickness, and sea ice thickness using averaged sea ice and snow albedo. dEdd–AD has been adopted by the sea ice physics library Icepack (https://github.com/CICE-Consortium/Icepack/wiki, last access: 22 July 2019), which is used by the Los Alamos sea ice model CICE (Hunke et al., 2010) and Model for Prediction Across Scales Sea Ice (MPAS-Seaice; Turner et al., 2019). CICE itself is used in numerous global and regional models.
SNICAR and dEdd–AD solve the multiple-scattering radiative transfer equations and provide much improved solar radiative representations for the cryosphere, though their separate development and implementation created an artificial divide for snow simulation. In ESMs that utilize both SNICAR and dEdd–AD, such as the Community Earth System Model (CESM, http://www.cesm.ucar.edu/, last access: 22 July 2019) and the Energy Exascale Earth System Model (E3SM, previously known as ACME, https://e3sm.org/, last access: 22 July 2019), the solar radiative properties of snow on land and snow on sea ice are computed separately via SNICAR and dEdd–AD. As a result, the same snow in nature has different solar radiative properties such as reflectance depending on which model represents it. These differences are model artifacts that should be eliminated so that snow has consistent properties across the Earth system.
In this paper, we evaluate the accuracy and biases of three two-stream models listed in Table 2, including the algorithms used in SNICAR and dEdd–AD, for representing reflectance and heating. In Sects. 2–4, we describe the radiative transfer algorithms and calculations performed in this work. The results and model intercomparisons are discussed in Sect. 5. In Sect. 6, we introduce a parameterization to reduce the simulated albedo and heating bias for solar zenith angles larger than 75∘. In Sect. 7, we summarize the major differences of algorithm implementations between SNICAR and dEdd–AD in ESMs. We use these results to develop and justify a unified surface shortwave radiative transfer method for all Earth system model components in the cryosphere, presented in Sect. 8.
In this section, we summarize the three two-stream models and the benchmark DISORT model with 16 streams. These algorithms are well documented in papers by Toon et al. (1989), Briegleb and Light (2007), Jin and Stamnes (1994), and Stamnes et al. (1988). Readers interested in detailed mathematical derivations should refer to those papers. We only include their key equations to illustrate the difference among two-stream models for discussion purposes.
2.1 SNICAR in land models CLM and ELM
SNICAR is implemented as the default snow shortwave radiative transfer scheme in CLM and the E3SM land model (ELM). It adopts the two-stream algorithms and the rapid solver developed by Toon et al. (1989) to compute the solar properties of multilayer snowpacks. These two-stream algorithms are derived from the general equation of radiative transfer in a plane-parallel media:
where Φ is azimuth angle, μ is the cosine of the zenith angle, and ϖ is single-scattering albedo. On the right-hand side, the three terms are intensity at optical depth τ, internal source term due to multiple scattering, and external source term S. For a purely external source at solar wavelengths S is
where πFs is incident solar flux, and μ0 is the incident direction of the solar beam. Integrating Eq. (1) over azimuth and zenith angles yields the general solution of two-stream approximations (Meador and Weaver, 1980). The upward and downward fluxes at optical depth τ of layer n can be represented as
where Λn, Γn, and Cn are known coefficients determined by the two-stream method, incident solar flux, and solar zenith angle; whereas k1n and k2n are unknown coefficients determined by the boundary conditions. For an N-layer snowpack, the solutions for upward and downward fluxes are coupled at layer interfaces to generate 2N equations with 2N unknown coefficients k1n and k2n. Combining these equations linearly generates a new set of equations with terms in tri-diagonal form that enables the application of a fast tri-diagonal matrix solver. With the solved coefficients, the upward and downward fluxes are computed at different optical depths (Eqs. 3a and 3b) and eventually the reflectance, transmittance, and absorption profiles of solar flux for any multilayer snowpack.
SNICAR itself implements all three two-stream algorithms in Toon et al. (1989): Eddington, quadrature, and hemispheric mean. In practical simulations, it utilizes the Eddington and hemispheric-mean approximations to compute the visible and near-IR snow properties, respectively (Flanner et al., 2007). In addition to its algorithms, SNICAR implements the delta transform of the fundamental input variable asymmetry factor (g), single-scattering albedo (ϖ), and optical depth (τ) to account for the strong forward scattering in snow (Eqs. 2a–2c, Wiscombe and Warren, 1980).
2.2 dEdd–AD in sea ice models Icepack, CICE, and MPAS-Seaice
Icepack, CICE, and MPAS-Seaice use the same shortwave radiative scheme dEdd–AD developed and documented by Briegleb and Light (2007). Sea ice is divided into multiple layers to first compute the single-layer reflectance and transmittance using two-stream delta-Eddington solutions to account for the multiple scattering of light within each layer (Equation set 50, Briegleb and Light, 2007), where the name “delta” implies dEdd–AD implements the delta transform to account for the strong forward scattering of snow and sea ice (Eqs. 2a–2c, Wiscombe and Warren, 1980). The single-layer direct albedo and transmittance are computed by equations
where coefficients An, Bn, Kn, En, Hn, and εn are determined by the single-scattering albedo (ϖ), asymmetry factor (g), optical depth (τ), and angle of the incident beam at layer n (μ0, n). Following the delta-Eddington assumption, simple formulas are available for the single-layer reflectance and transmittance under both clear sky (direct flux, Eqs. 4a and 4b) and overcast sky (diffuse flux) conditions. However, the formula derived by applying diffuse-flux upper boundary conditions sometimes yields negative albedos (Wiscombe, 1977). To avoid the unphysical values, diffuse reflectance and transmittance of a single layer are computed by integrating the direct reflectance R(μ) and transmittance T(μ) over the incident hemisphere assuming isotropic incidence:
This is the same as the method proposed by Wiscombe and Warren (1980, their Eq. 5). In practice, eight Gaussian angles are implemented to perform the integration for every layer.
The computed single-layer reflectance and transmittance of direct and diffuse components are then combined to account for the interlayer scattering of light to compute the reflectance and transmission at every interface (Equation set 51, Briegleb and Light, 2007), and eventually the upward and downward fluxes (Equation set 52, Briegleb and Light, 2007). These upward and downward fluxes at each optical depth are then used to compute the column reflectance and transmittance, and the absorption profiles for any multilayered media, such as snowpacks on land and sea ice.
In nature, a large fraction of sea ice is covered by snow during winter. As snow melts away in late spring and summer, it exposes bare ice, and melt ponds form on the ice surface. Such variation in sea ice surface types requires the shortwave radiative transfer model to be flexible and capable of capturing the light refraction and reflection. Refractive boundaries exist where air (refractive index mre=1.0), snow (assuming snow as medium of air containing a collection of ice particles, mre=1.0), pond (assuming pure water, mre=1.33), and ice (assuming pure ice, mre=1.31) are present in the same sea ice column. The general solution of delta-Eddington and the two-stream algorithms used in SNICAR are not applicable to such nonuniformly refractive layered media. To include the effects of refraction, Briegleb and Light (2007) modified the adding formula at the refractive boundaries (i.e., interfaces between air and ice, snow and ice, and air and pond). The reflectance and transmittance of the adjacent layers above and below the refractive boundary are combined with modifications to include the Fresnel reflection and refraction of direct and diffuse fluxes (Sect. 4.1, Briegleb and Light, 2007). dEdd–AD can thus be applied to any layered media with either uniform (e.g., snow on land) or nonuniform (e.g., snow on sea ice) refractive indexes.
In this paper, we apply dEdd–AD to snowpacks that can be treated as uniform refractive media such as the land snow columns assumed in SNICAR for model evaluation. An ideal radiative treatment for snow should, however, keep the potential to include refraction for further applications to snow on sea ice or ice sheets. Therefore, in addition to these two widely used algorithms in Icepack and SNICAR, we evaluate a third algorithm (Sect. 2.3) that can be applied to layered media with either uniform or nonuniform refractive indexes.
2.3 Two-stream discrete-ordinate algorithm (2SD)
A refractive boundary also exists between the atmosphere and the ocean, and models have been developed to solve the radiative transfer problems in the atmosphere–ocean system using the discrete-ordinate technique (e.g., Jin and Stamnes, 1994; Lee and Liou, 2007). Similar to the two-stream algorithms of Toon et al. (1989) used in SNICAR, Jin and Stamnes (1994) also developed their algorithm from the general equation
Equation (6) is the azimuthally integrated version of Eq. (1). However, for vertically inhomogeneous media like the atmosphere–ocean or sea ice, the external source term S(τ, μ) is different. Specifically, for the medium of total optical depth τa above the refractive interface, one must consider the contribution from the upward beam reflected at the refractive boundary (second term on the right-hand side):
where is the Fresnel reflectance of radiation and m is the ratio of the refractive indices of the lower to the upper medium. For the medium below the refractive interface, one must account for the Fresnel transmittance and modify the angle of beam travel in media b:
where μ0n is the cosine zenith angle of refracted beam incident at angle μ0 above the refractive boundary, by Snell's law:
For uniformly refractive media like snow on land, one can just set the refractive index mre equal to 1 for every layer. In this case, the Fresnel reflectance is 0 in Eq. (7), the Fresnel transmittance is 1 in Eq. (8), and μ0n equals μ0: the two source terms Sa(τ, μ) and Sb(τ, μ) become the same and equal the source term of homogenous media given in Eq. (2).
For two-stream approximations of this method, analytical solutions of upward and downward fluxes are coupled at each layer interface to generate 2N equations with 2N unknown coefficients for any N-layer stratified column. The solutions of two-stream algorithms and boundary conditions for homogenous media are well documented (Sect. 8.4 and 8.10 of Thomas and Stamnes, 1999). Despite the extra source terms, these 2N equations can also be organized into a tri-diagonal matrix similar to the method of Toon et al. (1989) used in SNICAR. Flexibility and speed therefore make this two-stream discrete-ordinate algorithm (hereafter, 2SD) a potentially good candidate for long-term Earth system modeling. In this work, we only apply 2SD to the snowpack and note that it can be applied to any uniformly or nonuniformly refractive media like snow on land or sea ice, with the delta transform implemented for fundamental optical variables (Eqs. 2a–2c, Wiscombe and Warren, 1980).
2.4 16-stream DISORT
In addition to the mathematical technique, the accuracy and speed of radiative transfer algorithms depend on the number of angles used for flux estimation in the upward and downward hemispheres. SNICAR, dEdd–AD, and 2SD use one angle to represent upward flux and one angle to represent downward flux; hence they are named the two-stream algorithm. Lee and Liou (2007) use two upward and two downward streams. Jin and Stamnes (1994) documented the solutions for any even number of streams. The computational efficiency of these models is lower than that of two-stream models while their accuracy is better. To quantify the accuracy of the three two-stream algorithms for snow shortwave simulations, we use the 16-stream DIScrete-Ordinate Radiative Transfer model (DISORT) as the benchmark model (http://lllab.phy.stevens.edu/disort/, last access: ) (Stamnes et al., 1988).
In this work, we focus on the performance of two-stream algorithms for pure snow simulations. The inputs for these three models are the same: single-scattering properties (SSPs, i.e., single-scattering albedo ϖ, asymmetry factor g, extinction coefficient σext) of snow determined by snow grain radius r, snow depth, solar zenith angle θ, solar incident flux, and the albedo of underlying ground (assuming Lambertian reflectance of 0.25 for all wavelengths). A delta transform is applied to fundamental input optical variables for all simulations (Eqs. 2a–2c, Wiscombe and Warren, 1980).
In snow, photon scattering occurs at the air–ice interface, and the absorption of photons occurs within the ice crystal. The most important factor that determines snow shortwave properties is the ratio of total surface area to total mass of snow grains, also known as “the specific surface area” (e.g., Matzl and Schneebeli, 2006, 2010). The specific surface area (β) can be converted to a radiatively effective snow grain radius r:
where ρice is the density of pure ice, 917 kg m−3. Assuming the grains are spherical, the SSPs of snow can thus be computed using Mie theory (Wiscombe, 1980) and ice optical constants (Warren and Brandt, 2008). In nature, snow grains are not spherical, and many studies have been carried out to quantify the accuracy of such spherical representations (Grenfell and Warren, 1999; Neshyba et al., 2003; Grenfell et al., 2005). In recent years, more research has been done to evaluate the impact of grain shape on snow shortwave properties (Dang et al., 2016; He et al., 2017, 2018a, b), and they show that nonspherical snow grain shapes mainly alter the asymmetry factor. Dang et al. (2016) also point out that the solar properties of a snowpack consisting of nonspherical ice grains can be mimicked by a snowpack consisting of spherical grains with a smaller grain size by factors up to 2.4. In this work, we still assume the snow grains are spherical, and this assumption does not qualitatively alter our evaluation of the radiative transfer algorithms.
The input SSPs of snow grains are computed using Mie theory at a fine spectral resolution for a wide range of ice effective radius r from 10 to 3000 µm that covers the possible range of grain radius for snow on Earth (Flanner et al., 2007). The same spectral SSPs were also used to derive the band-averaged SSPs of snow used in SNICAR. Note Briegleb and Light (2007) refer to SSPs as inherent optical properties.
In climate modeling, snow albedo computation at a fine spectral resolution is expensive and unnecessary. Instead of computing spectrally resolved snow albedo, wider-band solar properties are more practical. For example, CESM and E3SM aggregate the narrow RRTMG bands used for the atmospheric radiative transfer simulation into visible (0.2–0.7 µm) and near-IR (0.7–5 µm) bands. The land model and sea ice model thus receive visible and near-IR fluxes as the upper boundary condition, and return the corresponding visible and near-IR albedos to the atmosphere model. In practice, these bands are also partitioned into direct and diffuse components. Therefore, a practical two-stream algorithm should be able to simulate the direct visible, diffuse visible, direct near-IR, and diffuse near-IR albedos and absorptions of snow accurately.
The band albedo α is an irradiance-weighted average of the spectral albedo α(λ):
In this work, we use the spectral irradiance F(λ) generated by the atmospheric DISORT-based Shortwave Narrowband Model (SWNB2) (Zender et al., 1997; Zender, 1999) for typical clear-sky and cloudy-sky conditions of midlatitude winter as shown in Fig. 1a. The total clear-sky down-welling surface flux at different solar zenith angles are also given in Fig. 1b.
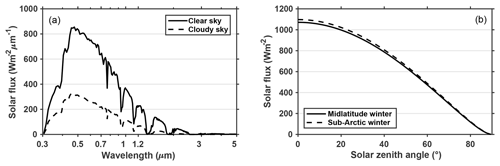
Figure 1Spectral and total down-welling solar flux at surface computed using SWNB2 for (a) standard clear-sky and cloudy-sky atmospheric profiles of midlatitude winter assuming solar zenith angle is 60∘ at the top of the atmosphere, and for (b) standard clear-sky profiles of midlatitude and sub-Arctic winter with different incident solar zenith angles.
5.1 Spectral albedo and reflected solar flux
The spectral reflectance of pure deep snow computed using two-stream models and 16-stream DISORT is shown in Fig. 2. The snow grain radius is 100 µm – a typical grain size for fresh new snow. For clear sky with a direct beam source (left column), all three two-stream models show good accuracy at visible wavelengths (0.3–0.7 µm), and within this band, the snow albedo is large and close to 1. As wavelength increases, the albedo diminishes in the near-IR band. Two-stream models overestimate snow albedo at these wavelengths, with maximum biases of 0.013 (SNICAR and dEdd–AD) and 0.023 (2SD) within wavelength 1–1.7 µm. For cloudy-sky cases with diffuse upper boundary conditions, dEdd–AD reproduces the snow albedo at all wavelengths with the smallest absolute error (<0.005), and SNICAR and 2SD both overestimate the snow albedo with maximum biases >0.04 between 1.1 and 1.4 µm.
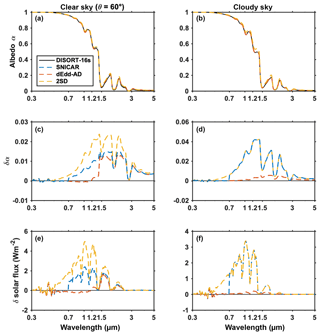
Figure 2The spectral albedo of pure snow computed using 16-stream DISORT, SNICAR, dEdd–AD, and 2SD models, for clear-sky (direct beam at solar zenith angle 60∘) and cloudy-sky conditions in the left and right panels, respectively. Panels (a, b) show spectral albedo. Panels (c, d) show the difference () in spectral albedos computed using the two-stream model (α2) and 16-stream DISORT (α16). Panels (e, f) show the difference of reflected spectral flux given δα. The snowpack is set to semi-infinite deep with a grain radius of 100 µm.
In both sky conditions, the errors of snow albedo are larger at near-IR wavelengths ranging from 1.0 to 1.7 µm, while the solar incident flux peaks at 0.5 µm then decrease as wavelength increases. The largest error in reflected flux is within the 0.7–1.5 µm band for SNICAR and 2SD, as shown in the third row of Fig. 2. dEdd–AD overestimates the direct snow albedo mostly at wavelengths larger than 1.5 µm where the error in reflected flux is almost negligible.
5.2 Broadband albedo and reflected solar flux
Integrated over the visible and near-IR wavelengths, the error in band albedos computed using two-stream models for different cases is shown in Figs. 3–6.
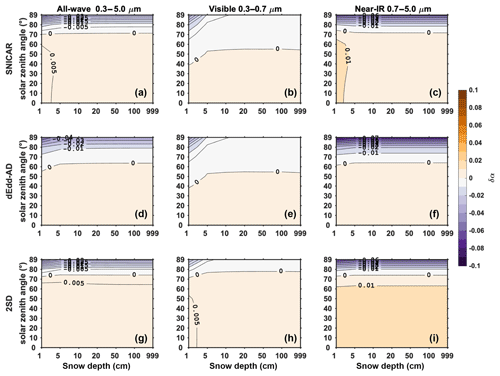
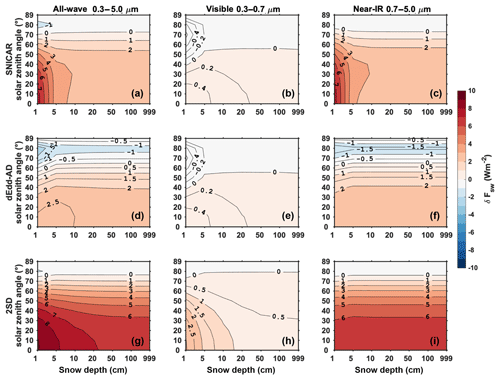
Figure 3The difference in direct snow albedo () computed using two-stream models (α2) and using the 16-stream DISORT model (α16), for various snow depths and solar zenith angles, with a snow grain radius of 100 µm. From the top to the bottom, rows are results of two-stream models SNICAR, dEdd–AD, and 2SD. From the left to the right columns are albedo differences of all-wave, visible, and near-IR bands.
Figure 3 shows the error in direct band albedo for fixed snow grain radius of 100 µm with different snow depth and solar zenith angles. As introduced in Sect. 2, SNICAR and dEdd–AD both use the delta-Eddington method to compute the visible albedo. They overestimate the visible albedo for solar zenith angles smaller than 50∘ by up to 0.005, and underestimate it for solar zenith angles larger than 50∘ by up to −0.01. 2SD produces similar results for the visible band but at a larger solar zenith angle threshold of 75∘. In the near-IR band, SNICAR and 2SD overestimate the snow albedo for solar zenith angles smaller than 70∘, beyond this, the error in albedo increases by up to −0.1 as solar zenith angle increases. dEdd–AD produces a similar error pattern with a smaller solar zenith angle threshold at 60∘. As snow ages, its average grain size increases. For typical old melting snow of grain radius 1000 µm (Fig. 4), two-stream models produce similar errors of direct albedo in all bands. Integrating over the entire solar band, the three two-stream models evaluated show similar error patterns for direct albedo.
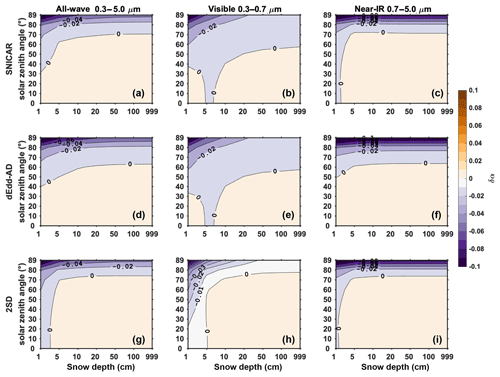
Figure 4The difference in direct snow albedo () computed using two-stream models (α2) and using the 16-stream DISORT model (α16), for various snow depths and solar zenith angles, with a snow grain radius of 1000 µm.
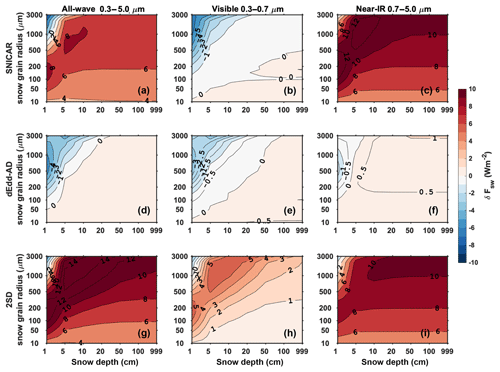
For a fixed solar zenith angle of 60∘, the error of direct albedo for different snow depth and snow grain radii is shown in Fig. 5. SNICAR and dEdd–AD underestimate the visible albedo in most scenarios, while 2SD overestimates the visible albedo for a larger range of grain radius and snow depth. All three two-stream models tend to overestimate the near-IR albedo except for shallow snow with large grain radius; the error of 2SD is 1 order of magnitude larger than that of SNICAR and dEdd–AD.
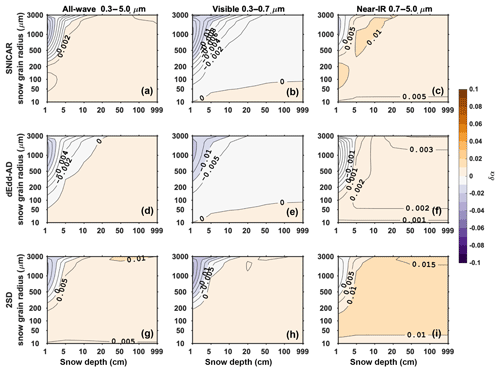
Figure 5The difference in direct snow albedo () computed using two-stream models (α2) and using the 16-stream DISORT model (α16), for various snow depths and snow grain radii, with a solar zenith angle of 60∘.
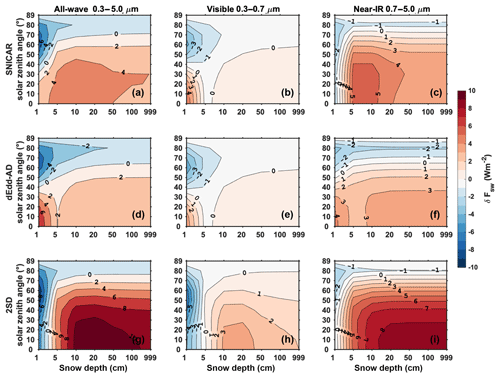
Figure 6 is similar to Fig. 5, but shows the diffuse snow albedo. In the visible band, SNICAR and dEdd–AD generate similar errors in that they both underestimate the albedo as snow grain size increases and snow depth decreases. 2SD overestimates the albedo with a maximum error of around 0.015. In the near-IR, two-stream models tend to overestimate snow albedo, while the magnitude of biases produced by SNICAR and 2SD is 1 order larger than that of dEdd–AD with the maximum error of 0.035 generated by SNICAR. As a result, the all-wave diffuse albedos computed using dEdd–AD are more accurate than those computed using SNICAR and 2SD.
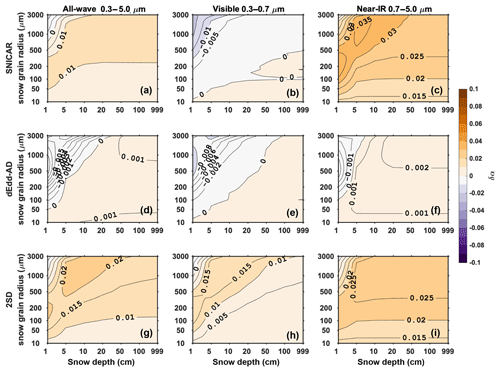
Figure 6The difference in diffuse snow albedo () computed using two-stream models (α2) and using the 16-stream DISORT model (α16), for various snow depths and snow grain radii, with a solar zenith angle of 60∘ at the top of the atmosphere.
Figures 7, 8, and 9 show the errors in reflected shortwave flux caused by snow albedo errors seen in Figs. 3, 4, and 6. In general, two-stream models produce larger errors in reflected direct near-IR flux (Figs. 7 and 8), especially with the 2SD model: the maximum overestimate of reflected near-IR flux is 6–8 W m−2 for deep melting snow with a solar zenith angle <30∘. Errors in reflected direct visible flux are smaller (mostly within ±1 W m−2) for all models in most scenarios, and become larger (mostly within ±3 W m−2) as snow grain size increases to 1000 µm if computed using 2SD. As shown in Fig. 9, for diffuse flux with a solar zenith angle of 60∘ at the top of the atmosphere (TOA), SNICAR and dEdd–AD generate small errors in reflected visible flux (mostly within ±1 W m−2), while 2SD always overestimates reflected visible flux by up to 5 W m−2. In the near-IR, SNICAR and 2SD overestimate reflected flux by as much as 10–12 W m−2; the error in reflected near-IR flux produced by dEdd–AD is much smaller, mostly within ±1 W m−2.
In general, dEdd–AD produces the most accurate albedo and thus reflected flux for both direct and diffuse components. SNICAR is similar to dEdd–AD for its accuracy of direct albedo and flux, yet generates large error for the diffuse component. 2SD tends to overestimate snow albedo and reflected flux in both direct and diffuse components and shows the largest errors among three two-stream models. Although the differences between algorithms are small, they can have a notable impact on snowpack melt. For example, compared to dEdd–AD, SNICAR and 2SD overestimate the diffuse albedo by ∼0.015 for melting snow (Fig. 6). In Greenland, the daily averaged downward diffuse solar flux from May to September is 200 W m−2, and the averaged cloud cover fraction is 80 % (Fig. 6, Dang et al., 2017). In this case, SNICAR and 2SD overestimate the reflected solar flux by 2.4 W m−2 d−1 – the amount of energy is otherwise enough to melt 10 cm of snow water equivalent from May to September. dEdd–AD also remediates compensating spectral biases (where visible and near-IR biases are of opposite signs) present in the other schemes. Those spectral biases do not affect the broadband fluxes like the diffuse biases, but they nevertheless degrade proper feedbacks between snow–ice reflectance and heating.
5.3 Band absorption of solar flux
Figure 10 shows absorption profiles of shortwave flux computed using the 16-stream DISORT model, with errors in absorbed fractional solar flux computed using two-stream models. The snowpack is 10 cm deep and is divided into five layers, each 2 cm thick. The snow grain radii are set to 100 µm and 1000 µm. The figure shows fractional absorption for snow layers 1–4 and the underlying ground with an albedo of 0.25.
As shown in the first column of Fig. 10, for new snow with a radius of 100 µm, most solar absorption occurs in the top 2 cm snow layer, where roughly 10 % and 15 % of diffuse and direct near-IR flux is absorbed and dominates the solar absorption within the snowpack. In the second layer (2–4 cm), the absorption of solar flux is less than 1 % and gradually decreases within the interior layers. The underlying ground absorbs roughly 2 % of solar flux, mostly visible flux that penetrates the snowpack more efficiently. As snow ages and snow grain grows, photons penetrate deeper into the snowpack. For typical old melting snow with a radius of 1000 µm, most solar absorption still occurs in the top 2 cm snow layer, where roughly 20 % and 14 % of diffuse and direct near-IR flux is absorbed. The second snow layer (2–4 cm) absorbs more near-IR solar flux by roughly 2 %. More photons can penetrate through the snowpack, and result in a high fractional absorption by the underlying ground, especially for the visible band. As snow depth increases, the ground absorption will decrease for both snow radii.
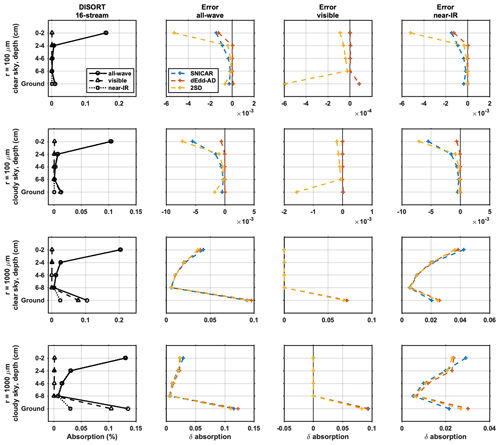
Figure 10Comparison of light-absorption profiles derived from two-stream models and 16-stream DISORT. The left-most column shows fractional band absorptions computed using 16-stream DISORT. The right three panels show the errors of all-wave, visible, and near-IR fractional absorptions calculated using two-stream models. The top and bottom panels are for clear-sky and cloudy-sky conditions (solar zenith angle of 60∘), respectively. The snowpack is 10 cm deep and is divided evenly into five 2 cm thick layers, for new snow (r=100 µm) and old snow (r=1000 µm). Layers 1–4 represent the top four snow layers (top 8 cm), and layer 5 represents underlying ground with an albedo of 0.25.
Comparing to 16-stream DISORT, two-stream models underestimate the column solar absorptions for new snow, and they overestimate them for old snow, especially for the surface snow layer and the underground. Overall, dEdd–AD gives the most accurate absorption profiles among the three two-stream models, especially for new snow.
It has been pointed out in previous studies that the two-stream approximations become poor as solar zenith angle approaches 90∘ (e.g., Wiscombe, 1977; Warren, 1982). As shown in Figs. 3 and 4, all three two-stream models underestimate the direct snow albedo for large solar zenith angles. In the visible band, when the snow grain size is small, the error in direct albedo is almost negligible (Fig. 3); while as snow ages and snow grains become larger, the error increases yet remains low if the snow is deep (Fig. 4). In the near-IR range, the biases of albedo are also larger for larger snow grain radii. For a given snow size, the magnitudes of such biases are almost independent of snow depth and mainly determined by the solar zenith angle. In general, the errors of all-wave direct albedo are mostly contributed by the errors of near-IR albedo, especially for optically thick snowpacks (i.e., semi-infinite), because the errors of direct albedo in the visible range are negligible compared with those in the near-IR range. To improve the performance of two-stream algorithms, we develop a parameterization that corrects the underestimated near-IR snow albedo at large zenith angles.
Figure 11 shows the direct near-IR albedo and fractional absorption of 2 m thick snowpacks consisting of grains with radii of 100 and 1000 µm, computed using two-stream algorithms and 16-stream DISORT. For solar zenith angles >75∘, two-stream models underestimate snow albedo and overestimate solar absorption within the snowpack, mostly in the top 2 cm of snow, and the differences among the three two-stream models are small. In Sect. 5, we have shown that dEdd–AD produces the most accurate snow albedo in general. With anticipated wide application of dEdd–AD, we develop the following parameterization to adjust its low biases in computed near-IR direct albedo.
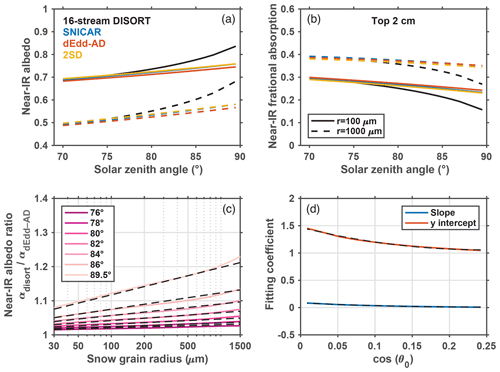
Figure 11(a) Direct near-IR snow albedo and (b) near-IR fractional absorption by top 2 cm snow of a 2 m thick snowpack, for solar zenith angles larger than 70∘ and snow grain radii of 100 and 1000 µm. (c) The ratios of near-IR albedo computed using dEdd–AD compared to those computed using 16-stream DISORT for different solar zenith angles. These ratios are parameterized as linear functions of the logarithmic of snow grain radius. The slopes and y intercepts are shown in (d). The black dashed curves in (c, d) are fitting values computed using parameterization discussed in Sect. 5.
We define and compute as the ratio of direct semi-infinite near-IR albedo computed using 16-stream DISORT (α16-DISORT) to that computed using dEdd–AD (αdEdd-AD), for solar zenith angle >75∘. This ratio is shown in Fig. 11c and can be parameterized as a function of snow grain radius (r, in meters) and the cosine of incident solar zenith angle (μ0), as shown in Fig. 11c:
where coefficients c1 and c0 are polynomial functions of μ0, as shown in Fig. 11d:
Since two-stream models always underestimate snow albedo, always exceeds 1 (Fig. 11c). We can then adjust the direct near-IR snow albedo (αdEdd-AD) and direct near-IR solar absorption (FabsdEdd-AD) by snow computed using dEdd–AD with ratio :
where Fnir is the direct near-IR flux. This adjustment reduces the error of near-IR albedo from negative 2 %–10 % to within ±0.5 % for solar zenith angles larger than 75∘, and for grain radii ranging from 30 to 1500 µm (Fig. 12). Errors in broadband direct albedo are therefore also reduced to <0.01. The direct near-IR flux absorbed by the snowpack decreases after applying this adjustment.
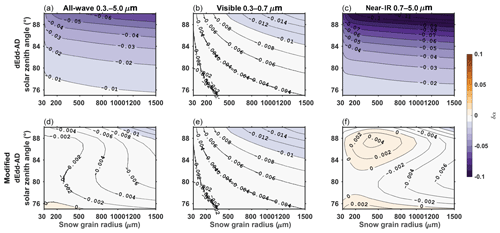
Figure 12Error in semi-infinite snow albedo computed using dEdd–AD before (a, b, c) and after (d, e, f) incorporating corrections for direct near-IR albedo, for different solar zenith angles and snow grain radii.
When the solar zenith angle exceeds 75∘, our model adjusts the computed direct near-IR albedo αdEdd−AD by the ratio following Eqs. (12)–(14a) and reduces direct near-IR absorption following Eq. (14b). If snow is divided into multiple layers, we assume all decreased near-IR absorption (second term on the right-hand side, Eq. 14b) is confined within the top layer. This assumption is fairly accurate for the near-IR band since most absorption occurs at the surface of the snowpack (Figs. 10 and 11). As discussed previously, this parameterization is developed based on albedo computed using dEdd–AD. For models that do not use dEdd–AD but SNICAR and 2SD, the same adjustment still applies given the small differences of near-IR direct albedo computed using two-stream models (Fig. 11). For models that adopt other radiative transfer algorithms it is best for the developers to examine their model against a benchmark model such as 16-stream DISORT or two-stream models discussed in this work before applying this correction.
Although the errors of direct near-IR albedos are large for large solar zenith angles, the absolute error in reflected shortwave flux is small (Figs. 7 and 8) as the down-welling solar flux reaches snowpack and decreases as solar zenith angle increases (Fig. 1b). However, such small biases in flux can be important for high latitudes where the solar zenith angle is large for many days in late winter and early spring.
ESMs often use band-averaged SSPs of snow and aerosols for computational efficiency, rather than using brute-force integration of spectral solar properties across each band (per Eq. 11). In addition to using different radiative transfer approximations, SNICAR and dEdd–AD also adopt different methods to derive the band-averaged SSPs of snow for different band schemes.
In SNICAR, snow solar properties are computed for five bands: one visible band (0.3–0.7 µm) and four near-IR bands (0.7–1, 1–1.2, 1.2–1.5, and 1.5–5 µm). The solar properties of four subdivided near-IR bands are combined by fixed ratios to compute the direct and diffuse near-IR snow properties. These two sets of ratios are derived offline based on the incident solar spectra typical of midlatitude winter for clear- and cloudy-sky conditions (Fig. 1a).
The band-averaged SSPs of snow grains are computed following the Chandrasekhar mean approach (Thomas and Stamnes, 1999, their Eq. 9.27; Flanner et al., 2007). Specifically, spectral SSPs of snow grains are weighted into bands according to surface incident solar flux typical of midlatitude winter for clear- and cloudy-sky conditions. In addition, the single-scattering albedo ϖ(λ) of ice grains is also weighted by the hemispheric albedo α(λ) of an optically thick snowpack:
Two sets of snow band-averaged SSPs are generated for all grain radii, suitable for direct and diffuse light. For each modeling step and band, SNICAR is called twice to compute the direct and diffuse snow solar properties.
In dEdd–AD, the snow-covered sea ice properties are computed for three bands: one visible band (0.3–07 µm) and two near-IR bands (0.7–1.19 and 1.19–5 µm). The solar proprieties of these two near-IR bands are combined using ratios wnir1 and wnir2 for 0.7–1.19 and 1.19–5 µm, depending on the fraction of direct near-IR flux fnidr:
The band SSPs of snow are derived by integrating the spectral SSPs and the spectral surface solar irradiance measured in the Arctic under mostly clear sky.
In addition, the band-averaged single-scattering albedo is also increased to until the band albedo computed using averaged SSPs matches the band albedo within 0.0001, where is
dEdd–AD adopts this single set of band SSPs for both direct and diffuse computations. In practice, the physical snow grain radius r is adjusted to a radiatively equivalent radius reqv based on the fraction of direct flux in the near-IR band (fnidr):
This reqv and the corresponding snow SSPs are then used in the radiative transfer calculation. The computed direct and diffuse solar properties alone are less accurate, while the combined all-sky broadband solar properties agree with SNICAR (Briegleb and Light, 2007). As a result, for each modeling step and band, the dEdd–AD radiative transfer subroutine is called only once to compute both the direct and diffuse snow solar properties simultaneously.
SNICAR and dEdd–AD also use different approaches to avoid numerical singularities. In SNICAR, singularities occur when the denominator of term in Eq. (3) equals zero (i.e., ), where γ is determined by the approximation method and SSPs of snow, and μ0 is the cosine of the solar zenith angle (Eqs. 23 and 24, Toon et al., 1989). When such a singularity is detected, SNICAR will shift μ0 by +0.02 or −0.02 to obtain physically realistic radiative properties. In the dEdd–AD algorithm, singularities arise only when μ0=0 (Eq. 4). Therefore, in practice, for μ0<0.01, dEdd–AD computes the sea ice solar properties for μ0=0.01 to avoid unphysical results.
Based on the intercomparison of three two-stream algorithms and their implementations in ESMs, we formulated the following surface shortwave radiative transfer recommendations for an accurate, fast, and consistent treatment for snow on land, land ice, and sea ice in ESMs.
First, the two-stream delta-Eddington adding–doubling algorithm by Briegleb and Light (2007) is unsurpassed as a radiative transfer core. The evaluation in Sect. 5 shows that this algorithm produces the least error for snow albedo and solar absorption within snowpack, especially under overcast skies. This algorithm applies well to both uniformly refractive media such as snow on land, and to nonuniformly refractive media, such as bare, snow-covered, and ponded sea ice and bare and snow-covered land ice. Numerical singularities occur only rarely (when μ0=0) and are easily avoided in model implementations. Among the three two-stream algorithms discussed here, dEdd–AD is also the most efficient one as it takes only two-thirds of the time of SNICAR and 2SD to compute solar properties of multilayer snowpacks.
Second, any two-stream cryospheric radiative transfer model can incorporate the parameterization described in Sect. 6 to adjust the low bias of direct near-IR snow albedo and high bias of direct near-IR solar absorption in snow, for solar zenith angles larger than 75∘. These biases are persistent across all two-stream algorithms discussed in this work, and should be corrected for snow-covered surfaces. Alternatively, adopting a four-stream approximation would reduce or eliminate such biases, though at considerable expense in computational efficiency.
Third, in a cryospheric radiative transfer model, one should prefer physically based parameterizations that are extensible and convergent (e.g., with increasing spectral resolution) for the band-averaged SSPs and size distribution of snow. Although the treatments used in SNICAR and dEdd–AD are both practical since they both reproduce the narrowband solar properties with carefully derived band-averaged inputs as discussed in Sect. 7, the snow treatment used in SNICAR is more physically based and reproducible since it does not rely on subjective adjustment and empirical coefficients as used in dEdd–AD. Specifically, the empirical adjustment to snow grain radius implemented in dEdd–AD may not always produce compensating errors. For example, in snow containing light-absorbing impurities such adjustment may also lead to biases in aerosol absorption since the albedo reduction caused by light-absorbing particles does not linearly depend on snow grain radius (Dang et al., 2015). For further model development incorporating nonspherical snow grain shapes (Dang et al., 2016; He et al., 2018a, b), such adjustment on grain radius may fail as well. Moreover, SNICAR computes the snow properties for four near-IR bands, which helps capture the spectral variation in albedo (Fig. 2) and therefore better represents near-IR solar properties. It is also worth noting that unlike the radiative core of dEdd–AD, SNICAR is actively maintained, with numerous modifications and updates in the past decade (e.g., Flanner et al., 2012; He et al., 2018b). Snow radiative treatments that follow SNICAR conventions for SSPs may take advantage of these updates. Note that any radiative core that follows SNICAR SSP conventions must be called twice to compute diffuse and direct solar properties.
Fourth, a surface cryospheric radiative transfer model should flexibly accommodate coupled simulations with distinct atmospheric and surface spectral grids. Both the five-band scheme used in SNICAR and the three-band scheme used in dEdd–AD separate the visible from near-IR spectrum at 0.7 µm. This boundary aligns with the Community Atmospheric Model's original radiation bands (CAM; Neale et al., 2010), though not with the widely used Rapid Radiative Transfer Model (RRTMG; Iacono et al., 2008), which places 0.7 µm squarely in the middle of a spectral band. A mismatch in spectral boundaries between atmospheric and surface radiative transfer schemes can require an ESM to unphysically apportion energy from the straddled spectral bin when coupling fluxes between surface and atmosphere. The spectral grids of surface and atmosphere radiation need not be identical so long as the coarser grid shares spectral boundaries with the finer grid. In practice maintaining a portable cryospheric radiative module such as SNICAR requires a complex offline toolchain (Mie solver, spectral refractive indices for air, water, ice, and aerosols, spectral solar insolation for clear and cloudy skies) to compute, integrate, and rebin SSPs. Aligned spectral boundaries between surface and atmosphere would simplify the development of efficient and accurate radiative transfer for the coupled Earth system.
Last, it is important to note that, although we only examine the performance of the dEdd–AD for pure snow in this work, this algorithm can be applied to the surface solar calculation of all cryospheric components with or without light-absorbing particles present. First, Briegleb and Light (2007) proved its accuracy for simulating ponded and bare sea ice solar properties against observations and a Monte Carlo radiation model. Second, In CESM and E3SM, the radiative transfer simulation of snow on land ice is carried out by SNICAR with prescribed land ice albedo. Adopting the dEdd–AD radiative core in SNICAR will permit these ESMs to couple the snow and land ice as a nonuniformly refractive column for more accurate solar computations since bare, snow-covered, and ponded land ice is physically similar to bare, snow-covered, and ponded sea ice, and the latter is already treated well by the dEdd–AD radiative transfer core. Third, adding light-absorbing particles in snow will not change our results qualitatively. Both dEdd–AD and SNICAR simulate the impact of light-absorbing particles (black carbon and dust) on snow and/or sea ice using self-consistent particle SSPs that follow the SNICAR convention (e.g., Flanner et al., 2007; Holland et al., 2012). These particles are assumed to be either internally or externally mixed with snow crystals; the combined SSPs of mixtures (e.g., Appendix A of Dang et al., 2015) are then used as the inputs for radiative transfer calculation. The adoption of the dEdd–AD radiative transfer algorithm in SNICAR, and the implementation of SNICAR snow SSPs in dEdd–AD enables a consistent simulation of the radiative effects of light-absorbing particles in the cryosphere across ESM components.
In summary, this intercomparison and evaluation has shown multiple ways that the solar properties of cryospheric surfaces can be improved in the current generation of ESMs. We have merged these findings into a hybrid model SNICAR-AD, which is primarily composed of the radiative transfer scheme of dEdd–AD, five-band snow–aerosol SSPs of SNICAR, and the parameterization to correct for snow albedo biases when solar zenith angle exceeds 75∘. This hybrid model can be applied to snow on land, land ice, and sea ice to produce consistent shortwave radiative properties for snow-covered surfaces across the Earth system. With the evolution and further understanding of snow and aerosol physics and chemistry, the adoption of this hybrid model will obviate the effort to modify and maintain separate optical variable input files used for different model components.
SNICAR-AD is now implemented in both the sea ice (MPAS-Seaice) and land (ELM) components of E3SM. More simulations and analyses are underway to examine its impact on E3SM model performance and simulated climate. The results are however beyond the scope of this work and will be thoroughly discussed in a future paper.
In this work, we aim to improve and unify the solar radiative transfer calculations for snow on land and snow on sea ice in ESMs by evaluating the following two-stream radiative transfer algorithms: the two-stream delta-Eddington adding–doubling algorithm dEdd–AD implemented in sea ice models Icepack, CICE, and MPAS-Seaice, the two-stream delta-Eddington and two-stream delta-Hemispheric-Mean algorithms implemented in snow model SNICAR, and a two-stream delta-discrete-ordinate algorithm. Among these three models, dEdd–AD produces the most accurate snow albedo and solar absorption (Sect. 5). All two-stream models underestimate near-IR snow albedo and overestimate near-IR absorption when solar zenith angles are larger than 75∘, which can be adjusted by a parameterization we developed (Sect. 6). We compared the implementations of radiative transfer cores in SNICAR and dEdd–AD (Sect. 7) and recommended a consistent and hybrid shortwave radiative model SNICAR-AD for snow-covered surfaces across ESMs (Sect. 8). Improved treatment of surface cryospheric radiative properties in the thermal infrared has recently been shown to remediate significant climate simulation biases in polar regions (Huang et al., 2018). It is hoped that adoption of improved and consistent treatments of solar radiative properties for snow-covered surfaces as described in this study will further remediate simulation biases in snow-covered regions.
The data and models are available upon request to Cheng Dang (cdang5@uci.edu). SNICAR and dEdd–AD radiative transfer core can be found at https://github.com/E3SM-Project/E3SM (last access: 22 July 2019).
CD and CZ designed the study. CD coded the offline dEdd-AD and 2SD schemes, performed two-stream and 16-stream model simulations, and wrote the paper with input from CZ and MF. CZ performed the SWNB2 simulations. MF provided the base SNICAR code and snow optical inputs.
The authors declare that they have no conflict of interest.
The authors thank Stephen G. Warren and Qiang Fu for insightful discussions on radiative transfer algorithms. The authors thank Adrian Turner for instructions on installing and running MPAS-Seaice. The authors thank David Bailey and the one anonymous reviewer for their constructive comments that improved our paper. This research is supported as part of the Energy Exascale Earth System Model (E3SM) project, funded by the U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research.
This research has been supported by the U.S. Department of Energy (grant no. DE-SC0012998).
This paper was edited by Dirk Notz and reviewed by David Bailey and one anonymous referee.
Aoki, T., Kuchiki, K., Niwano, M., Kodama, Y., Hosaka, M., and Tanaka, T.: Physically based snow albedo model for calculating broadband albedos and the solar heating profile in snowpack for general circulation models, J. Geophys. Res., 116, D11114, https://doi.org/10.1029/2010JD015507, 2011.
Bøggild, C. E., Brandt, R. E., Brown, K. J., and Warren, S. G.: The ablation zone in northeast Greenland: ice types, albedos and impurities, J. Glaciol., 56, 101–113, https://doi.org/10.3189/002214310791190776, 2010.
Brandt, R. E., Warren, S. G., Worby, A. P., and Grenfell, T. C.: Surface albedo of the Antarctic sea ice zone, J. Climate, 18, 3606–3622, https://doi.org/10.1175/JCLI3489.1, 2005.
Briegleb, P. and Light, B.: A Delta-Eddington mutiple scattering parameterization for solar radiation in the sea ice component of the community climate system model, NCAR Technical Note NCAR/TN-472+STR, https://doi.org/10.5065/D6B27S71, 2007.
Dang, C. and Hegg, D. A.: Quantifying light absorption by organic carbon in Western North American snow by serial chemical extractions, J. Geophys. Res.-Atmos., 119, 10247–10261, https://doi.org/10.1002/2014JD022156, 2014.
Dang, C., Brandt, R. E., and Warren, S. G.: Parameterizations for narrowband and broadband albedo of pure snow and snow containing mineral dust and black carbon, J. Geophys. Res.-Atmos., 120, 5446–5468, https://doi.org/10.1002/2014JD022646, 2015.
Dang, C., Fu, Q., and Warren, S. G.: Effect of snow grain shape on snow albedo, J. Atmos. Sci., 73, 3573–3583, https://doi.org/10.1175/JAS-D-15-0276.1, 2016.
Dang, C., Warren, S. G., Fu, Q., Doherty, S. J., Sturm, M., and Su, J.: Measurements of light-absorbing particles in snow across the Arctic, North America, and China: Effects on surface albedo, J. Geophys. Res.-Atmos., 122, 10149–10168, https://doi.org/10.1002/2017JD027070, 2017.
Doherty, S. J., Warren, S. G., Grenfell, T. C., Clarke, A. D., and Brandt, R. E.: Light-absorbing impurities in Arctic snow, Atmos. Chem. Phys., 10, 11647–11680, https://doi.org/10.5194/acp-10-11647-2010, 2010.
Doherty, S. J., Dang, C., Hegg, D. A., Zhang, R., and Warren, S. G.: Black carbon and other light-absorbing particles in snow of central North America, J. Geophys. Res.-Atmos., 119, 12807–12831, https://doi.org/10.1002/2014JD022350, 2014.
Doherty, S. J., Hegg, D. A., Johnson, J. E., Quinn, P. K., Schwarz, J. P., Dang, C., and Warren, S. G.: Causes of variability in light absorption by particles in snow at sites in Idaho and Utah, J. Geophys. Res.-Atmos., 121, 4751–4768, https://doi.org/10.1002/2015JD024375, 2016.
Flanner, M. G. and Zender, C. S.: Snowpack radiative heating: Influence on Tibetan Plateau climate, Geophys. Res. Lett., 32, L06501, https://doi.org/10.1029/2004GL022076, 2005.
Flanner, M. G., Zender, C. S., Randerson, J. T., and Rasch, P. J.: Present-day climate forcing and response from black carbon in snow, J. Geophys. Res., 112, D11202, https://doi.org/10.1029/2006JD008003, 2007.
Flanner, M. G., Liu, X., Zhou, C., Penner, J. E., and Jiao, C.: Enhanced solar energy absorption by internally-mixed black carbon in snow grains, Atmos. Chem. Phys., 12, 4699–4721, https://doi.org/10.5194/acp-12-4699-2012, 2012.
Gardner, A. S. and Sharp, M. J.: A review of snow and ice albedo and the development of a new physically based broadband albedo parameterization, J. Geophys. Res., 115, F01009, https://doi.org/10.1029/2009JF001444, 2010.
Grenfell, T. C. and Warren S. G.: Representation of a nonspherical ice particle by a collection of independent spheres for scattering and absorption of radiation, J. Geophys. Res., 104, 31697–31709, https://doi.org/10.1029/1999JD900496, 1999.
Grenfell, T. C., Neshyba, S. P., and Warren, S. G.: Representation of a nonspherical ice particle by a collection of independent spheres for scattering and absorption of radiation: 3. Hollow columns and plates, J. Geophys. Res., 110, D17203, https://doi.org/10.1029/2005JD005811, 2005.
He, C., Takano, Y., Liou, K. N., Yang, P., Li, Q., and Chen, F.: Impact of Snow Grain Shape and Black Carbon–Snow Internal Mixing on Snow Optical Properties: Parameterizations for Climate Models, J. Climate, 30, 10019–10036, https://doi.org/10.1175/JCLI-D-17-0300.1, 2017.
He, C., Liou, K. N., Takano, Y., Yang, P., Qi, L., and Chen, F.: Impact of grain shape and multiple black carbon internal mixing on snow albedo: Parameterization and radiative effect analysis, J. Geophys. Res.-Atmos., 123, 1253–1268, https://doi.org/10.1002/2017JD027752, 2018a.
He, C., Flanner, M. G., Chen, F., Barlage, M., Liou, K.-N., Kang, S., Ming, J., and Qian, Y.: Black carbon-induced snow albedo reduction over the Tibetan Plateau: uncertainties from snow grain shape and aerosol–snow mixing state based on an updated SNICAR model, Atmos. Chem. Phys., 18, 11507–11527, https://doi.org/10.5194/acp-18-11507-2018, 2018b.
Holland, M. M., Bailey, D. A., Briegleb, B. P., Light, B., and Hunke, E.: Improved sea ice shortwave radiation physics in CCSM4: The impact of melt ponds and aerosols on Arctic sea ice, J. Climate, 25, 1413–1430, 2012.
Huang, X., Chen, X., Flanner, M., Yang, P., Feldman, D., and Kuo, C.: Improved representation of surface spectral emissivity in a global climate model and its impact on simulated climate, J. Climate, 31, 3711–3727, 2018.
Hunke, E. C., Lipscomb, W. H., Turner, A. K., Jeffery, N., and Elliott, S.: CICE: the Los Alamos Sea Ice Model, Documentation and Software User's Manual, Version 4.1, LA-CC-06-012, T-3 Fluid Dynamics Group, Los Alamos National Laboratory, Los Alamos NM, USA, 2010.
Iacono, M. J., Delamere, J. S., Mlawer, E. J., Shephard, M. W., Clough, S. A., and Collins, W. D.: Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models, J. Geophys. Res., 113, D13103, https://doi.org/10.1029/2008JD009944, 2008.
Jin, Z. and Stamnes, K.: Radiative transfer in nonuniformly refracting layered media: atmosphere–ocean system, Appl. Optics, 33, 431–442, https://doi.org/10.1364/AO.33.000431, 1994.
Kuipers Munneke, P., Van den Broeke, M. R., Lenaerts, J. T. M., Flanner, M. G., Gardner, A. S., and Van de Berg, W. J.: A new albedo parameterization for use in climate models over the Antarctic ice sheet, J. Geophys. Res., 116, D05114, https://doi.org/10.1029/2010JD015113, 2011.
Lee, W. L. and Liou, K. N.: A coupled atmosphere–ocean radiative transfer system using the analytic four-stream approximation, J. Atmos. Sci., 64, 3681–3694, https://doi.org/10.1175/JAS4004.1, 2007.
Liang, S., Fang, H., Chen, M., Shuey, C. J., Walthall, C., Daughtry, C., Morisette, J., Schaaf, C., and Strahler, A.: Validating MODIS land surface reflectance and albedo products: Methods and preliminary results, Remote Sens. Environ., 83, 149–162, https://doi.org/10.1016/S0034-4257(02)00092-5, 2002.
Light, B., Grenfell, T. C., and Perovich, D. K.: Transmission and absorption of solar radiation by Arctic sea ice during the melt season, J. Geophys. Res., 113, C03023, https://doi.org/10.1029/2006JC003977, 2008.
Light, B., Perovich, D. K., Webster M. A., Polashenski, C., and Dadic, R.: Optical properties of melting first-year Arctic sea ice, J. Geophys. Res.-Oceans, 120, 7657–7675, https://doi.org/10.1002/2015JC011163, 2015.
Marshall, S. and Oglesby, R. J.: An improved snow hydrology for GCMs. Part 1: Snow cover fraction, albedo, grain size, and age, Clim. Dynam., 10, 21–37, https://doi.org/10.1007/BF00210334, 1994.
Marshall, S. E.: A Physical Parameterization of Snow Albedo for Use in Climate Models, NCAR Cooperative thesis 123, National Center for Atmospheric Research, Boulder, CO, 175 pp. 1989.
Marshall, S. E. and Warren S. G., Parameterization of snow albedo for climate models, in: Large Scale Effects of Seasonal Snow Cover, edited by: Goodison, B. E., Barry, R. G., and Dozier, J., International Association of Hydrological Sciences, Washington, D. C., IAHS Publ., vol. 166, 43–50, 1987.
Matzl, M. and Schneebeli, M.: Measuring specific surface area of snow by near-infrared photography, J. Glaciol., 52, 558–564, https://doi.org/10.3189/172756506781828412, 2006.
Matzl, M. and Schneebeli, M.: Stereological measurement of the specific surface area of seasonal snow types: Comparison to other methods, and implications for mm-scale vertical profiling, Cold Reg. Sci. Tech., 64, 1–8, https://doi.org/10.1016/j.coldregions.2010.06.006, 2010.
Meador, W. E. and Weaver, W. R.: Two-stream approximations to radiative transfer in planetary atmospheres: A unified description of existing methods and a new improvement, J. Atmos. Sci., 37, 630–643, https://doi.org/10.1175/1520-0469(1980)037<0630:TSATRT>2.0.CO;2, 1980.
Mlawer, E. J. and Clough, S. A.: On the extension of rapid radiative transfer model to the shortwave region: in: Proceedings of the 6th Atmospheric Radiation Measurement (ARM) Science Team Meeting, US Department of Energy, CONF-9603149, 223–226, 1997.
Neale, R. B., Chen, C.-C., Gettelman, A., Lauritzen, P. H., Park, S., Williamson, D. L., Conley, A. J., Garcia, R., Kinnison, D., Lamarque, J. F., and Marsh, D.: Description of the NCAR community atmosphere model (CAM 5.0), NCAR Technical Note, NCAR/TN-486+STR, 1, 1–12, 2010.
Neshyba, S. P., Grenfell, T. C., and Warren, S. G.: Representation of a nonspherical ice particle by a collection of independent spheres for scattering and absorption of radiation: 2. Hexagonal columns and plates, J. Geophys. Res., 108, 4448, https://doi.org/10.1029/2002JD003302, 2003.
Perovich, D. K.: The optical properties of sea ice, Monograph 96-1, Cold Regions Research & Engineering Laboratory, US Army Corps of Engineers, Hanover, NH, USA, 1996.
Stamnes, K., Tsay, S. C., Wiscombe, W., and Jayaweera, K.: Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media, Appl. Optics, 27, 2502–2509, https://doi.org/10.1364/AO.27.002502, 1988.
Thomas, G. and Stamnes, K.: Radiative Transfer in the Atmosphere and Ocean (Cambridge Atmospheric and Space Science Series), Cambridge University Press Cambridge, https://doi.org/10.1017/CBO9780511613470, 1999.
Toon, O. B., McKay, C. P., Ackerman, T. P., and Santhanam, K.: Rapid calculation of radiative heating rates and photodissociation rates in inhomogeneous multiple scattering atmospheres, J. Geophys. Res., 94, 16287–16301, https://doi.org/10.1029/JD094iD13p16287, 1989.
Turner, A. K., Lipscomb, W. H., Hunke, E. C., Jacobsen, D. W., Jeffery, N., Ringler, T. D., and Wolfe, J. D.: MPAS-Seaice: a new variable resolution sea-ice model, J. Adv. Model Earth Sy., in preparation, 2019.
Wang, X., Doherty, S. J., and Huang, J.: Black carbon and other light-absorbing impurities in snow across Northern China, J. Geophys. Res.-Atmos., 118, 1471–1492, https://doi.org/10.1029/2012JD018291, 2013.
Warren, S. G.: Optical properties of snow, Rev. Geophys., 20, 67–89, https://doi.org/10.1029/RG020i001p00067, 1982.
Warren, S. G. and Brandt, R. E.: Optical constants of ice from the ultraviolet to the microwave: A revised compilation, J. Geophys. Res., 113, D14220, https://doi.org/10.1029/2007JD009744, 2008.
Warren, S. G. and Wiscombe, W. J.: A model for the spectral albedo of snow. II: Snow containing atmospheric aerosols, J. Atmos. Sci., 37, 2734–2745, https://doi.org/10.1175/1520-0469(1980)037<2734:AMFTSA>2.0.CO;2, 1980.
Warren, S. G. and Wiscombe, W. J.: Dirty snow after nuclear war, Nature, 313, 467–470, https://doi.org/10.1038/313467a0, 1985.
Wiscombe, W. J.: The delta-Eddington approximation for a vertically inhomogeneous atmosphere, NCAR Technical Note, NCAR/TN-121+STR, https://doi.org/10.5065/D65H7D6Z, 1977.
Wiscombe, W. J.: Improved Mie scattering algorithms, Appl. Optics, 19, 1505–1509, https://doi.org/10.1364/AO.19.001505, 1980.
Wiscombe, W. J. and Warren, S. G.: A model for the spectral albedo of snow. I: Pure snow, J. Atmos. Sci., 37, 2712–2733, https://doi.org/10.1175/1520-0469(1980)037<2712:AMFTSA>2.0.CO;2, 1980.
Zender, C. S.: Global climatology of abundance and solar absorption of oxygen collision complexes,J. Geophys. Res., 104, 24471–24484, https://doi.org/10.1029/1999JD900797, 1999.
Zender, C. S., Bush, B., Pope, S. K., Bucholtz, A., Collins, W. D., Kiehl, J. T., Valero, F. P., and Vitko Jr., J.: Atmospheric absorption during the atmospheric radiation measurement (ARM) enhanced shortwave experiment (ARESE), J. Geophys. Res., 102, 29901–29915, https://doi.org/10.1029/97JD01781, 1997.
- Abstract
- Introduction
- Radiative transfer model
- Input for radiative transfer models
- Solar spectra used for the spectral integrations
- Model evaluation
- Correction for direct albedo for large solar zenith angles
- Implementation of snow radiative transfer model in Earth system models
- Towards a unified radiative transfer model for snow, sea ice, and land ice
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Radiative transfer model
- Input for radiative transfer models
- Solar spectra used for the spectral integrations
- Model evaluation
- Correction for direct albedo for large solar zenith angles
- Implementation of snow radiative transfer model in Earth system models
- Towards a unified radiative transfer model for snow, sea ice, and land ice
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References