the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Role of discrete water recharge from supraglacial drainage systems in modeling patterns of subglacial conduits in Svalbard glaciers
Léo Decaux
Mariusz Grabiec
Dariusz Ignatiuk
Jacek Jania
As the behavior of subglacial water plays a determining role in glacier dynamics, it requires particular attention, especially in the context of climate warming, which is increasing ablation and generating greater amounts of meltwater. On many glaciers, water flowing from the glacier's surface is the main source of supply to the subglacial drainage system. This system is largely influenced by the supraglacial drainage system, which collects meltwater and precipitation and rapidly delivers it to discrete points in the glacier bed via moulins and crevassed areas, called water input areas (WIAs). Models of patterns of subglacial conduits mainly based on the hydrological potential gradient are still regularly performed without taking into account the supraglacial drainage system. We modeled the pattern of subglacial channels in two glaciers located in Svalbard, the land-terminating Werenskioldbreen and the tidewater Hansbreen during the 2015 melt season. We modeled a spatial and a discrete water recharge in order to compare them. First, supraglacial catchments were determined for each WIA on a high-resolution digital elevation model using the standard watershed modeling tool in ArcGIS. Then, interpolated water runoff was calculated for all the main WIAs. Our model also accounts for several water pressure conditions. For our two studied glaciers, during the ablation season 2015, 72.5 % of total runoff was provided by meltwater and 27.5 % by precipitation. Changes in supraglacial drainage on a decadal timescale are observed in contrast to its nearly stable state on an annual timescale. Nevertheless, due to the specific nature of those changes, it seems to have a low impact on the subglacial system. Therefore, our models of subglacial channel are assumed to be valid for a minimum period of two decades and depend on changes in the supraglacial drainage system. Results showed that, for Svalbard tidewater glaciers with large crevassed areas, models of subglacial channels that assume spatial water recharge may be somewhat imprecise but are far from being completely incorrect, especially for the ablation zone. On the other hand, it is important to take discrete water recharge into account in the case of land-terminating Svalbard glaciers with limited crevassed areas. In all cases, considering a discrete water recharge when modeling patterns of theoretical subglacial channels seems to produce more realistic results according to current knowledge.
In the context of global climate change and, in particular, the rapid melting of glaciers around the world, it is essential to understand changes in their meltwater drainage system and its consequences for glacier behavior. Today it is even more important to focus on the hydrological system of Arctic glaciers given that the Intergovernmental Panel on Climate Change (IPCC) predict longer summer seasons (Pachauri et al., 2014) and also knowing that Svalbard glaciers have already been shrinking for several decades (Błaszczyk et al., 2013; Hagen et al., 2003b). All predictions assume an increase in runoff (meltwater and precipitation) from Arctic glaciers, ice caps and ice sheets, suggesting intensification of their whole drainage system and consequently of their dynamics and their impact on sea level rise (Hagen et al., 2003a; Hanna et al., 2008; Mair et al., 2002; Nuth et al., 2010; Sundal et al., 2011). Meltwater and precipitation water are directly linked to glacier dynamics by supplying the subglacial drainage system, which lubricates the ice–bed interface, thereby reducing the basal shear stress resisting ice flow (Bartholomew et al., 2012; Hoffman et al., 2011; Shepherd et al., 2009). In the case of tidewater glaciers, an increase in velocity means an increase in calving rate and hence a higher loss of mass, thereby contributing even more to sea level rise. While Greenland and Antarctica are currently considered to be the main future players controlling sea level rise (DeConto and Pollard, 2016; Price et al., 2011; Rignot et al., 2011), it is crucial to understand how supraglacial, englacial and subglacial drainage systems influence each other in a glacier system, as this knowledge will make it possible to improve ice sheet models.
Nowadays, several models of subglacial conduits do not take the supraglacial drainage system into account (Fischer et al., 2005; Grabiec, 2017; Hagen et al., 2000; How et al., 2017; Pälli et al., 2003; Sharp et al., 1993; Shreve, 1972; Willis et al., 2009). As a result, they consider a spatial recharge (the term recharge is used here to refer to meltwater and precipitation water entering in the subglacial drainage system from the surface of the glacier), meaning that the water recharge is homogeneous or with some local water values over the entire surface of the glacier. This is one of the biggest assumptions that leads to inaccurate modeling of the locations of subglacial channels (Gulley et al., 2012).
However, due to their direct impact on the englacial and subglacial drainage system, studying supraglacial drainage systems is vital. Knowledge of these systems makes it possible to locate where the supraglacial system switches to an englacial and then subglacial system via moulins, shear fractures or crevasses, called water input areas (WIAs) and hence better estimates their water recharge (Bartholomew et al., 2011; Benn et al., 2017). Indeed, concentrated surface water streams are necessary for the formation of a channelized internal drainage system (Mavlyudov, 2006). Likewise, the supraglacial drainage system largely influences the subglacial system by collecting meltwater and precipitation water and rapidly delivering it to discrete points in the glacier bed via WIAs (Catania and Neumann, 2010; Gulley, 2009; Poinar et al., 2015; Smith et al., 2015). In addition to being an important source of water for the internal drainage system of glaciers, part of the englacial conduits are formed by direct incision of supraglacial channels followed by creep closure (Gulley et al., 2009; Irvine-Fynn et al., 2011). Nevertheless, the supraglacial drainage system remains one of the least studied hydrologic processes on Earth (Smith et al., 2015).
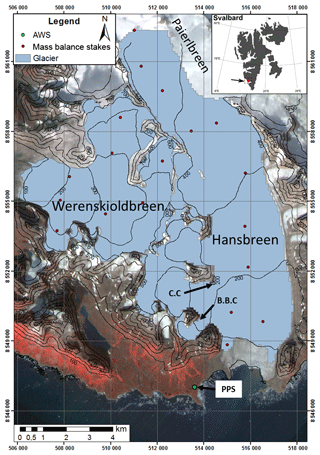
Figure 1Map showing the locations of Hansbreen and Werenskioldbreen, Svalbard, the automatic weather station (AWS), the Polish Polar Station (PPS), the mass balance stakes network, Crystal Cave (CC) and Bird Brain Cave (BBC). The background map is a SPOT satellite image acquired on 16 August 1988 and the coordinate system used is WGS 1984 UTM zone 33∘ N.
Spatial recharge is theoretical and is not actually observed on any glacier. Consequently, some models have used discrete recharge but only refer to limited areas on a glacier or with randomly placed moulins or even as a model validation method (Hewitt, 2013; Werder et al., 2013). In fact, no precise representation of the entire supraglacial drainage system (including inputs from both crevasses and moulins) has been used to constrain a subglacial channel model. Finally, no comparison study on the consequences of assuming spatial recharge has been performed.
Our study focused on the land-terminating glacier Werenskioldbreen and the tidewater glacier Hansbreen, both located in the southern part of the Svalbard archipelago and representative of many Svalbard glaciers (Fig. 1).
The first step consisted of identifying and mapping the supraglacial drainage features of the two glaciers using very high-resolution remote-sensing images for the years 1990, 2010, 2011 and 2015. Combining them with field observations allowed us to locate water flows inside the glaciers via moulins and crevasses (Benn et al., 2017, 2009; Holmlund, 1988; Nienow and Hubbard, 2006; Van der Veen, 2007). In the second step of this study, we calculated the catchment area of each main WIA on both glaciers. Subsequently we estimated the total amount of surface water (precipitation and meltwater) on the whole surface area of the two glaciers together with their surrounding slopes for the entire 2015 ablation season. This allowed us to map the locations of WIAs along with their absolute water recharge volumes. The final step consisted of modeling the pattern of subglacial conduits in the two glaciers using spatial recharge and discrete recharge for comparison.
Our attempt should improve the current modeling of the theoretical pattern of subglacial channels. More specifically, we discuss our results with the subglacial conduit models proposed by Pälli et al. (2003) and Grabiec (2017) for our two study glaciers, as these are only based on the hydrological potential gradient (Fischer et al., 2005; Flowers and Clarke, 2002; Sharp et al., 1993; Shreve, 1972). Moreover, contrasting model results with spatial and discrete water recharge enable a better understanding of the influence of this parameter for all glaciers.
2.1 Study sites
Two different types of polythermal Svalbard glaciers were chosen because their morphology, surface and subglacial topography, dynamics, thermal state and hydrology are representative of important types of Svalbard glaciers (Grabiec et al., 2012b; Hagen et al., 1993, 2003a, Ignatiuk et al., 2014). Werenskioldbreen is a land-terminating glacier and Hansbreen a tidewater one. They are characterized by two different dynamics that have a direct impact on changes in both the surface topography and the drainage system. Werenskioldbreen is located in southwest Spitsbergen (77∘05′ N, 15∘15′ E) (Fig. 1) and flows from east to west with an average speed of less than 10 m yr−1 in two parallel flows divided by a central moraine (Baranowski, 1970; Grabiec et al., 2012a). It is a quite small Svalbard glacier, 6.5 km long and 2.2 km wide, with a surface area of 27.1 km2 between 40 and 650 m a.s.l. (Ignatiuk et al., 2014; Majchrowska et al., 2015). It has a maximum thickness of about 275 m and a cold-ice snout less than 50 m thick, frozen to the bedrock up to 700 m upstream from the front line (Navarro et al., 2014; Pälli et al., 2003). Its entire surface is composed of cold ice (below the pressure melting point) overlying a temperate ice layer (at the pressure melting point) (Grabiec, 2017), thereby enabling the presence of a well-developed supraglacial drainage system (Ryser et al., 2013). Hansbreen, located at the entrance of Hornsund (77∘04′ N, 15∘38′ E) (Fig. 1), flows north to south with a velocity of ca. 150 m yr−1 at the front and of 55–70 m yr−1 3.7 km upstream (Błaszczyk et al., 2009). Situated between 0 and 664 m a.s.l., it is a medium-sized Svalbard glacier, 15.6 km long, ca. 2.5 km wide on average with a surface area of 53 km2. Its terminus forms a ca. 30 m high cliff 1.9 km in width, ending directly in the sea (Błaszczyk et al., 2009). Its mean ice thickness is 171 m and its maximum ice thickness is 386 m (Grabiec et al., 2012b). Temperate ice, firn and snow are present in the large accumulation area, allowing water to percolate down to the surface of the temperate ice and preventing the formation of supraglacial channels. The structure of the ablation area is similar to that of Werenskioldbreen, with a cold-ice layer overlying temperate ice (Grabiec, 2017; Navarro et al., 2014), preventing dispersed infiltration of the water below the equilibrium line altitude (ELA). However, most of the surface is crevassed, thereby limiting the development of a supraglacial drainage system. Crystal Cave and Bird Brain Cave located on Hansbreen (Fig. 1) are the only two well-studied and well-mapped intraglacial drainage systems in our study area (Gulley et al., 2012; Murray et al., 2007; Schroeder, 1998; Turu, 2012).
2.2 Datasets
We used very high-resolution (VHRS) WorldView-2 satellite images, with 0.5 m resolution, acquired on 21 August 2015 and Geoeye satellite images acquired on 10 August 2010. We also worked with sets of Norwegian Polar Institute aerial photos from 1990 and 2011. In addition to remote-sensing data, field observations and a Global Positioning System (GPS) survey, were necessary to identify control points to calibrate mapping. Maps of the supraglacial drainage system already exist for Werenskioldbreen in 1990 and 2010 (Ignatiuk, 2012; Pulina et al., 1999). Bedrock digital elevation models (DEMs) of Hansbreen and Werenskioldbreen at a spatial resolution of 100 m and a vertical resolution estimated at ±5 m, were obtained during a survey conducted in April 2008 by the University of Silesia and Institute of Geophysics Polish Academy of Sciences teams, combining GPS and GPR (ground-penetrating radar) measurements (Grabiec et al., 2012b). We also created a high-resolution surface DEM of both glaciers, using WorldView-2 VHRS images for the year 2015. Finally we used a meteorological dataset from the automatic weather station (AWS) located at the Polish Polar Station (PPS) (about 1.5 km from Hansbreen front) to calculate the volume of water produced by melt and precipitation during the 2015 melt season (Fig. 1).
3.1 Mapping supraglacial drainage
Based on high-resolution images, we generated several maps of the supraglacial drainage system of the two glaciers for different years using ArcMap software.

Figure 2Hansbreen (a) and Werenskioldbreen (b) WIA catchments in 2015. The background of the map is a WorldView-2 VHRS image acquired on 21 August 2015.
We mapped the surface streams manually, leading to personal choices and naturally to some subjective decisions. We decided to map only active streams with a minimum width of 1 m, knowing from field observations that numerous smaller streams are present, along with the limitation due to the spatial resolution of the VHRS images. In addition, we manually mapped crevassed areas and moulins with diameters greater than 1 m, enhanced by direct field observations and GPS measurements.
3.2 Calculation of WIA catchments
First, based on the supraglacial maps (Sect. 3.1), we created 2015 WIA maps for both glaciers (Fig. 2). WIAs were defined as substantial crevassed areas or crevassed areas intersecting active surface streams and groups of active moulins. In the large accumulation area of Hansbreen, water percolates through the snowpack, then through the firn, to finally create a layer of saturated water at the temperate ice–firn interface (Fountain and Walder, 1998; Lliboutry, 1971). The water flows along this interface, comes to the surface at the ELA or reaches the englacial system of the ablation area thanks to crevasses in the accumulation zone. Because the area situated just below the ELA is considered a WIA (large crevassed zone), we included the water from the accumulation area in it.
Next, the WorldView-2 stereo pair image from 2015 was processed with Geomatica software to create a surface DEM of our study area. The resulting DEM with a 4 m spatial resolution was delineated for both glaciers thanks to contour files obtained from orthorectified WorldView-2 images with a vertical accuracy of ±1.5 m. We filled in the small sinks on the DEM caused by small imperfections that occurred while we were creating the DEM, giving the impression that small lakes formed on the surface, which has never been observed in the second part of the ablation season on either glacier. From the corrected DEM, we calculated the flow direction from each pixel to its steepest downslope neighbor.
Finally, using standard watershed modeling tool in ArcGIS, we determined the water catchment area of each WIA with 4 m spatial resolution (Fig. 2). Some manual adjustments of the catchment delineations were made when necessary. The most common correction was to extend the catchment area where an active stream ending in a WIA was not included in it.
3.3 Estimation of spatially distributed runoff
The main subglacial water source is known to be controlled by runoff water from the surface of the glacier, mainly surface meltwater and precipitation (Flowers and Clarke, 2002; Hodson et al., 1998; Irvine-Fynn et al., 2011). Therefore, to create a quantitative subglacial water flow model, we extrapolated the amount of meltwater generated by the entire surface of the glacier and the amount of the total precipitation (solid, mixed and liquid) falling on the entire surface of the glacier and on the surrounding slopes for the 2015 melt season (6 June to 10 October 2015). Considering all types of precipitation allows us to take into account the potential meltwater originating from summer accumulation (due to solid and mixed precipitation). In fact, we assumed that all snow deposited during the ablation period will melt due to the positive average temperature over this season. Regarding the large accumulation area of Hansbreen, a large part of the water stored in the firn due to internal accumulation was included in our model. Thanks to a study by Grabiec (2017), we disposed of an estimation of the refreezing of capillary and percolation meltwater (excluding capillary water that freezes in the fall) in the snow and firn. It was estimated that from September 2007 to September 2008, 38 % of the total meltwater refroze in the snow and firn located above the ELA. Therefore, in our calculations, we considered that 38 % of the total meltwater in this area was trapped within the firn, corresponding to 5.5 × 106 m3 for the year 2015.
Spatial distribution in the surface ablation model was generated based on the summer mass balance data provided by the World Glacier Monitoring Service (WGMS), relying on the mass balance stake network present on both glaciers (Fig. 1) (Błaszczyk et al., 2019). WGMS provides data on accumulation and ablation points on the glaciers (WGMS, 2017). Surface ablation data combine meltwater produced by the winter snow cover at the beginning of the melt season, and glacier surface melt during the rest of the melting period. The relationship identified between the summer mass balance and elevation (R2=0.83) allowed us to model meltwater production (QM) for the whole glacier. Surface ablation was approximated by interpolation of stake data over the area (grid 100×100 m) at a range of elevations.
In the precipitation model, spatial distribution was calculated as follows. By applying a precipitation gradient (ΔP) of 19 % per 100 m (including catching error) calculated by Nowak and Hodson (2013) to the precipitation measured at the PPS (Q0), we were able to calculate the amount of precipitation (QP) at each altitude (h), in any DEM cell using Eq. (1):
Therefore, by combining the meltwater produced by the whole glacier with the amount of precipitation at each altitude, we were able to calculate the total glacier runoff (QH) in any DEM cells following Eq. (2):
Surface ablation modeling errors () were calculated using the standard error of the regression. Errors in the spatial distribution of the precipitation model () were calculated using the method of total differential function according to Eq. (3):
where σh is the DEM error and the precipitation measurement error at the PPS.
Therefore, we were able to calculate the total glacier runoff error according to Eq. (4):
We are aware that the error of precipitation spatial distribution is possibly larger due to expected substantial meteorological variations between rainfall events. However, the total calculated glacier runoff error coincides with Nowak and Hodson (2013) estimations. Moreover, it should be kept in mind that we might have underestimated the total amount of water runoff due to storage of liquid water in the snowpack and in the firn layer during the winter–spring period, which is released during the melt season (Arnold et al., 1998).
3.4 Subglacial modeling
The theoretical pattern of subglacial channels was modeled for the year 2015. This required knowledge of the surface and bedrock topography of the glacier (Sect. 2.2) and of the spatial distribution of ice thickness resulting from them. The spatial resolution of our model was limited by the 100 m resolution of the bedrock DEMs. We consequently had to upscale surface DEMs (Sect. 2.2), WIA catchment maps (Sect. 3.2) and the spatially distributed water runoff model (Sect. 3.3) in a 100 m grid. Surface and bedrock DEMs had a vertical accuracy of a few meters, which does not have much impact on our results with respect to the resolution of the spatial model (Fischer et al., 2005).
Water is known to circulate on, in and under glaciers in response to the hydraulic potential gradient (Shreve, 1972). Many models, and particularly the latest theoretical pattern of subglacial channels modeled by Grabiec (2017) and Pälli et al. (2003), are based on this gradient. We also based our model on this gradient, except that we considered that water circulation depends not only on the hydraulic potential gradient but also on some glaciological components. Subglacial drainage patterns can be modeled by assuming a spatially uniform flotation fraction K, which is the ratio between water pressure (Pw) and ice overburden pressure (Pi) (Flowers and Clarke, 1999) according to Eq. (5):
Therefore, as gridded values of surface and bedrock elevation can be used to model the subglacial drainage pattern from calculated hydraulic potential field Φ, we used Eq. (6):
where ρw is water density (1000 kg m−3), ρi is ice density (917 kg m−3), g is the acceleration due to gravity (9.81 m s−2), zb and zs are respectively bed and surface elevation.

Figure 3Spatial water recharge (meltwater and precipitation) for Hansbreen (a) and Werenskioldbreen (b) in 2015. The map background is a WorldView-2 VHRS image acquired on 21 August 2015.
The direction of subglacial water flow was determined based on the hydraulic potential field (Φ calculated for each grid cell). Water flows perpendicularly to the equipotential lines of the hydraulic potential field. We calculated the flow direction in each cell by identifying the neighboring cell with the lowest hydraulic potential value. The next step in the simulation calculates accumulated flow into each grid cell according to our flow direction model. The grid cells with the highest accumulation shape the lines of preferred water flow. Several models stop at this stage, in which the cell value denotes a cumulative number of cells due to the water inflow to this specific cell. Such a model may be able to successfully predict the location of plumes in front of a tidewater glacier (How et al., 2017). In order to go one step further, knowing the size of the cell, the value can easily be transferred to a drained surface area. In order to quantify the water drained through the system, the total amount of meltwater and precipitation (QH) in the 2015 melt season was calculated and assigned to each grid cell, as described in Sect. 3.3. The cells' values were then accumulated as described above, giving concentrated flow lines and water values through specific cells.
3.5 Model runs
We created two different simulation scenarios to take some glaciological and meteorological components into account:
-
Hydraulic potential (ablation and precipitation input). This model considers a spatial recharge of water, all the grid cells of the model are weighted as a function of the spatially distributed water runoff model values (QH) (Sect. 3.3) (Fig. 3). It corresponds to the last stage of the theoretical pattern of subglacial channels models achieved in our study area by Grabiec (2017) and Pälli et al. (2003) but updated for the year 2015 and with water volume values.
-
WIA (ablation and precipitation input). This model considers a discrete recharge of water, all the grid cells of the model corresponding to a WIA are weighted by the total amount of runoff (QH) (Sect. 3.3) occurring on their particular catchment (Sect. 3.2). All the other grid cells of the model are weighted with a value equal to 0 (Fig. 4). (Furthermore, in order to study the proportion of melt and precipitation water, the model has been run considering either the amount of meltwater – QM – or the amount of precipitation – QP.)
Accordingly for scenario (2), the volume of water reaching each moulin or crevasse area was calculated. It depended not only on the surface topography but also on the surface conditions such as bare ice, firn and snow.
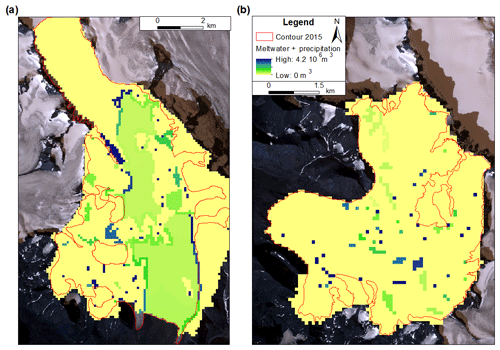
Figure 4Discrete water recharge (meltwater and precipitation) for Hansbreen (a) and Werenskioldbreen (b) in 2015. The map background is a WorldView-2 VHRS image acquired on 21 August 2015.
Water pressure in conduits depends directly on discharge (Röthlisberger, 1972) that, in turn, relies on recharge. Therefore, water pressure in conduits is directly affected by the available amount of surface water (melt and precipitation) and Majchrowska et al. (2015) observed marked fluctuations in melt and precipitation rates during the ablation seasons from 2007 to 2012 on Werenskioldbreen. High-pressure events (water pressure at ice overburden pressure) have been observed in the internal drainage system of Hansbreen at the beginning of intense melting periods (mainly in June and July) (Benn et al., 2009; Pälli et al., 2003; Schroeder, 1998; Vieli et al., 2004); and artesian features and overpressurized water outflows have been observed on Werenskioldbreen (Baranowski, 1977). Consequently, we modeled the subglacial channels for different K values (K=1, K=0.85, K=0.75, K=0.5, K=0.25, K=0) for the two different scenarios for both glaciers, resulting in 24 simulations.
Therefore, our model considers the following:
- i.
the surface properties of the glacier and hence the location of runoff and water percolation areas,
- ii.
the supraglacial drainage catchment structure of the glacier with respect to the WIAs and hence the volumes of runoff along particular drainage pathways,
- iii.
the water volume (meltwater plus precipitation) input to the system throughout the ablation season,
- iv.
several water pressure K scenarios in the channels, mainly to illustrate distinct periods of the melt season.
In theory, a subglacial drainage system of glaciers involves a distributed and channelized system (Kessler and Anderson, 2004). Because most subglacial water transport occurs in conduits, sustained by the balance between the creep closure effect and melting due to heat released by the water flux (Hewitt, 2011; Nye, 1953; Röthlisberger, 1972), we did not include the distributed part of the subglacial drainage system but focused on the channelized component.
4.1 Temporal changes in the supraglacial drainage system
The mapping of the supraglacial drainage systems of the two glaciers in 2015 only included crevassed areas, moulins, superficial percolation zones and runoff places leading to the WIAs used in our model (Fig. 2). However, maps of the whole supraglacial drainage system (including surface streams) for different years were only produced for Werenskioldbreen. In fact unlike Hansbreen, it has limited crevassed areas sustaining a well-developed supraglacial drainage system that allowed us to study the changes it has undergone.
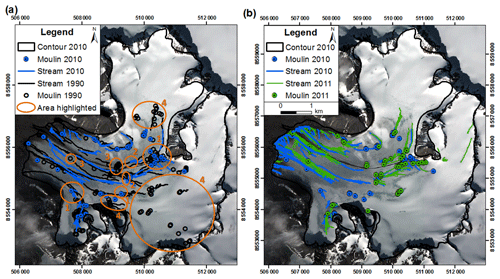
Figure 5Comparison of the supraglacial drainage system for Werenskioldbreen on a decadal timescale (a) and on an annual timescale (b). Explanations for the numbers are given in the text. The map background is a GeoEye-1 VHRS image acquired on 10 August 2010 and the coordinate system used is WGS 1984 UTM zone 33∘ N.
We compared the supraglacial drainage system of Werenskioldbreen on two different timescales, annual (2010–2011) and decadal (1990–2010). Changes in the glacier's geometry were observed in this period (Gajek et al., 2009; Ignatiuk et al., 2014). The supraglacial hydrology of glaciers depends directly on the surface topography (Grabiec et al., 2012b; Nienow and Hubbard, 2006). A change in the supraglacial drainage system would therefore be expected on the decadal timescale, giving us the opportunity to better understand the physical mechanisms controlling it. Figure 5a shows the different supraglacial drainage features for the years 1990 (black) and 2010 (blue). First, it is clearly visible that the surface streams are consistent for the 2 years, especially on the lower part of the glacier. Then several changes in the system can be observed, identified by numbers in Fig. 5a:
-
creation of new moulins deactivating downstream surface streams,
-
occurrence of new crevasses or shear fractures deactivating downstream surface streams,
-
abandoned moulins due to their flowing out of a depression area because of the glacier's motion or due to the deactivation of upstream surface streams,
-
the impossibility of mapping the surface drainage features due to thick snow cover at the end of the 2010 ablation season.
Figure 5b shows the different supraglacial features in the years 2010 (blue) and 2011 (green). The two supraglacial drainage systems are more consistent, and some small differences can be distinguished due to the snow cover, which made it impossible to map exactly the same areas.
4.2 Modeling the theoretical pattern of subglacial channels
The results of the simulations of scenarios (1) mentioned in Sect. 3.4 represent the first improvement to the model of our study area mentioned in this article: we now have a quantitative model compared to the previous models of Grabiec (2017) and Pälli et al. (2003), which are only qualitative.
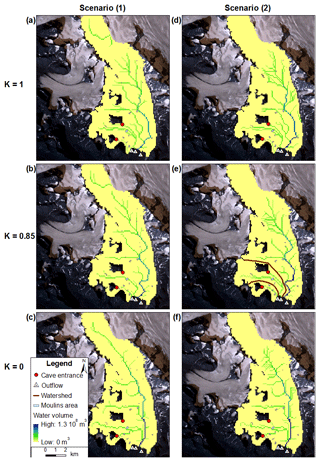
Because all the simulation results for K<0.85 display almost the same subglacial conduits pattern and clear differences are visible between results for K=0.85 and K=1, we only consider three water pressure states of simulations in this study, K=1, K=0.85 and K<0.85, represented here by K=0 (Figs. 6 and 7). The three other states K=0.25, K=0.5 and K=0.75 are given in the Appendix section (Figs. A1 and A2).
Spatial and discrete water recharge maps (Fig. 6) showed very similar results for Hansbreen, except that Crystal Cave and Bird Brain Cave conduits were better represented with a discrete water recharge. In the simulations, no subglacial channels started at these two locations, as is the case in reality when considering a spatial water recharge. In all cases, a general northwest to southeast subglacial water flow exists with one main channel in the eastern part of the glacier. Near the glacier front, the main flow direction changes from northeast to southwest. In the simulations in which K=0 (Fig. 6c and f), all the channels are connected to the main channel and have the same outflow at the glacier front. Simulations in which K=0.85 (Fig. 6b and e) and K=1 (Fig. 6a and d) show three outflows. The two eastern ones are consistent with the simulations, but the western one is located further west when K=1 than when K=0.85 (Fig. 6a and d). In all the scenarios, except scenario (1) with K=0, the main subglacial channel is generated just below the firn line (Fig. 6).
Concerning Werenskioldbreen, compared to scenario (1) (Fig. 7a–c), scenario (2) (Fig. 7d–f) displays a more dendritic channel network in the central part of the glacier and the conduits start at lower elevations. All the simulations show a main channel flowing in the central part of the glacier, with the same outflows when K=1 (Fig. 7a and d) and K=0 (Fig. 7c and f), and an outflow located further south when K=0.85 (Fig. 7b and e). Scenario (1), in which K=1, shows five outflows (Fig. 7a), whereas in scenario (2) three outflows are modeled (Fig. 7d). In the simulations in which K=0.85, three outflows are visible in scenario (1) (Fig. 7b) and two outflows in scenario (2) (Fig. 7e). When K=0, both scenarios exhibit only one outflow (Fig.7c and f). Compared to the previous model proposed by Pälli et al. (2003), none of our model scenarios suggest a subglacial flow separated by the medial moraine present on Werenskioldbreen.
Overall, compared to spatial recharge results, discrete recharge maps exhibit conduits starting at lower elevations with additional subglacial branches, meaning they match the location of the moulins and small crevassed areas better.
We attempted to automate surface stream mapping, as already achieved for Greenland by Yang and Smith (2013), using a specific normalized difference water index for the ice surface (NDWIice). NDWIice uses a normalized ratio of blue and red bands that allows each glacier pixel to be classified as either “water” or “nonwater”. The fact that it was not successful has several explanations. First, supraglacial streams in Svalbard glaciers are much smaller than those in Greenland. Second, Svalbard glaciers are surrounded by mountains that influence the surface conditions of the glaciers, which is not the case for the Greenland ice sheet. The surfaces of Svalbard glaciers are “dirty”; i.e., they contain many small rocks or dust that blow down the mountain slopes and land on the surface of the glaciers, changing the reflectance properties of the surface's features into a broadband signal rather than a well-separated signal specific to each feature. Indeed, looking at optical satellite images, surface streams in Greenland appear as a wide blue line overlying clean ice, which is not the case for Svalbard glacier's streams. Moreover, in Svalbard, there is extensive ice foliation and a network of shear fractures caused by friction with the surrounding mountains that closely resemble surface streams.
The consistency of surface streams on a decadal timescale (Fig. 5a), especially on the lower part of Werenskioldbreen, could be explained by the weak dynamics of the front and the fact that the longer a stream remains active and the deeper it carves into the glacier's surface, the more likely it is to survive. Despite these similarities, we observed several changes in the supraglacial drainage system on a decadal timescale in response to changes in geometry caused by climate warming and glacier flow. The occurrence of new moulins and new crevasses has a direct impact on the subglacial drainage system by creating new WIAs followed by potentially new subglacial channels. Abandoned moulins also deactivate the englacial and subglacial conduits they previously supplied with water (Holmlund, 1988; Nienow et al., 1998; Poinar et al., 2015). In the absence of internal water pressure and erosion, such conduits may then be closed by ice deformation. Nevertheless, observed supraglacial changes do not seem to imply a complete reorganization of the subglacial system (e.g., like after a surge event). In fact, new WIAs are either in relatively close proximity (about 300 m2) to the old ones or on the same subglacial channels axes as the pre-existing ones. This is especially the case with abandoned moulins, which are deactivated by new moulins a short distance up-glacier.
It is therefore crucial to investigate the permanency of the supraglacial drainage system of this glacier because it determines the validity of the duration of our model. Supraglacial drainage patterns are relatively persistent on an annual timescale (Fig. 5b) as expected from the study of Nienow and Hubbard (2006). Their study suggests that a subglacial drainage system remains relatively steady from year to year. Finally, considering the low impact of decadal timescale changes in the supraglacial drainage system (Fig. 5a) on the subglacial system, we can consider that our model is valid, with some minor changes, for a minimum period of 20 years. Results of the subglacial drainage system modelled for the year 1936 and the period 2005–2008 by Grabiec (2017) reinforced our statement by displaying only a few changes regarding the subglacial patterns and the outflow locations.
The three different water pressure states of simulations described in Sect. 4.2 may be representative of two different melt season periods:
-
K=1 and K=0.85 may represent the beginning of the melt season when a considerable amount of water is delivered to the hydrological system due to melting of the winter snow mantle. It may also illustrate heavy rainfall and ice melt events. In these conditions, the channels are filled or nearly filled with water, Pw=Pi or Pw=0.85Pi, and water flow may be mainly controlled by the surface topography of the glacier (Flowers and Clarke, 1999).
-
K<0.85 may represent all the other periods of the melt season. Especially after a high melting event (K value will be close to 0), the conduits will have been extensively enlarged, caused by the walls melting due to the frictional heat released by an intense turbulent water flow, combined with a small water input volume. Under such conditions, the channels are not full of water, Pw<Pi and the water flow may be controlled mainly by the bedrock topography of the glacier (Hagen et al., 2000; Sharp et al., 1993).
The total calculated volume of water entering Hansbreen over the whole of the 2015 melt season is m3, of which 74 % is meltwater and 26 % precipitation. Taken together, the theoretical patterns of modelled subglacial channels indicate that most of the water is drained by a main conduit located on the east side of the glacier (Fig. 6). Both scenarios exhibit more or less the same subglacial conduits in the ablation area as a result of a heavily crevassed surface. In fact, in scenario (2) most of the glacier surface in this area is considered a WIA (Fig. 2a), whereas in scenario (1) the entire surface is considered a WIA. Therefore, in scenario (2), only 47 % of the total water input volume, of the ablation area, is drained in a discrete manner, whereas the percentage for Werenskioldbreen is 100 % (Fig. 4). This is due to the fact that, in general, tidewater glaciers are more crevassed than land-terminating glaciers because their greater dynamics are related to the difference in the morphology of their fronts (Larsen et al., 2007; Moon and Joughin, 2008; Van der Veen, 2007), whereas their subglacial hydrology system is very similar. However, scenario (1) displays some subglacial channels in the accumulation area, while scenario (2) does not. This is the main improvement represented by our results, in considering a discrete water recharge for this type of glacier. Scenario (2), in which K=0.85 (Fig. 6e), is most in agreement with field observations. In fact, it is the only scenario that represents the well-studied subglacial channels generated by Crystal Cave and Bird Brain Cave (Gulley et al., 2012; Murray et al., 2007; Schroeder, 1998; Turu, 2012), with a coherent orientation compared to existing maps (Benn et al., 2009; Mankoff et al., 2017) and the authors' personal observations, along with the best location of outflows. In fact, the authors visited those two cave systems several times a year for a few years and repeated observations confirmed that the data cited above are still valid. However, the locations of the modeled outflows do not correspond perfectly with our observations and the one made by Grabiec (2017) and Pälli et al. (2003) (locations of sediment plumes, turbid water spots and visible R-channel). This is due to a lack of GPR data at the glacier front because of the presence of too many crevasses. The three outflows have their own water catchments and therefore drain different amounts of water (Fig. 6e). According to our results, the western outflow drained 2.7 % of the total water volume, the central outflow 14.8 % and the eastern one 82.5 %.
The total calculated volume of water entering Werenskioldbreen over the whole 2015 melt season is m3 of which 68.7 % is meltwater and 31.3 % is precipitation. The total annual runoff from the Werenskioldbreen basin from 2007 to 2012 measured by Majchrowska et al. (2015) ranged between 56.37 and 98.71×106 m3. First, there is notable variability from year to year. Second, the Werenskioldbreen basin considered in the study by Majchrowska et al. (2015) included the glacier forefield, meaning their study area was larger than ours. Third, we only considered the runoff from 6 June to 10 October 2015, not for the whole year. Finally, we underestimate the total runoff by only taking the water derived from precipitation and surface melting into account. For these reasons, we can be quite satisfied with our modeled value, which is of about the same order of magnitude as those measured in the preceding years. Regarding our distribution of water sources, we can also be quite satisfied when we compare it with calculations made by Majchrowska et al. (2015). In 2009, total runoff comprised 71 % meltwater, 17 % precipitation and 9 % other sources, and in 2011 it was 63 % meltwater, 28 % precipitation and 9 % other sources. All the model results of the theoretical pattern of subglacial channels indicate that most of the water is drained by a main conduit located in the central part of the glacier, the outflow of which is located further south of the medial moraine (Fig. 7). Both scenarios produce different results because of the low glacier dynamics leading to a poorly crevassed surface resulting in considerable differences in water recharge between the spatial (Fig. 3b) and the discrete (Fig. 4b) test cases. Scenario (2), in which K=1 (Fig. 7d) with one outflow located in the northern part of the medial moraine and two outflows in its southern part, best matches field observations. In fact, the modeled locations of the outflows in this simulation fit our observations quite well and the one made by Grabiec (2017), Majchrowska et al. (2015) and Pälli et al. (2003) (location of streams in the glacier forefield). The three outflows have their own water catchments and therefore drain different amounts of water (Fig. 7d). The northern one drained 35 % of the total water, the central one 51.6 % and the southern one 13.4 %. The fact that our model does not appear to be influenced by the Werenskioldbreen medial moraine, unlike the model of Pälli et al. (2003), may be due to the new geometry of the glacier in 2015 compared to that in 1999. However, some dye-tracing measurements have shown that subglacial water can flow across this medial moraine area during about the same modeling period as that used in the study by Pälli et al. (2003). Regarding Werenskioldbreen's moulins, we observed that those located at higher elevations are supplied by more precipitation than meltwater, contrary to the moulins located at lower elevations; e.g., two moulins situated at 420 m a.s.l. are supplied by 69 % meltwater and 31 % precipitation and one moulin situated at 112 m a.s.l. is supplied by 85.7 % meltwater and 14.3 % precipitation. Such observation shows that water recharge regarding melt and precipitation water proportion is heterogeneous on the glacier surface. This tendency was not observed on Hansbreen, probably due to its less steep slope and the smaller range of elevation of the cold-ice surface compared to Werenskioldbreen.
The fact that discrete recharge models generate subglacial channels starting at lower elevations and prevent any conduits from being generated in the accumulation area may be consistent with reality. In fact, we know that water does not penetrate the bare-ice surface of a glacier without the presence of crevasses or moulins (Fountain and Walder, 1998; Hodgkins, 1997; Lliboutry, 1971; Paterson, 1994; Ryser et al., 2013), and that water percolates through the snowpack and the firn to flow at the temperate ice–firn interface, and also that WIAs are mainly located in the central part of the two glaciers we studied. In some simulations of Hansbreen with scenario (1) (Figs. 6a, b and A1a), we observed a subglacial channel in the accumulation area flowing outside the glacier in an eastern glacier system belonging to Paierlbreen. This could be an artefact due to the boundary of our model, which does not allow Paierlbreen's drainage system to influence the Hansbreen drainage system, but not necessarily. In fact, since Paierlbreen surged in 2006, the ice division was drained downslope, thereby reducing Paierlbreen's ice pressure on Hansbreen and facilitating the flow of water from the upper part of the Hansbreen system to the Paierlbreen system rather than the other way around. Therefore, it may fit to the reality to observe this state under high water pressure conditions (K=1, K=0.85 and K=0.75) (Figs. 6a, b and A1a) and not under atmospheric or low water pressure conditions (K=0, K=0.25 and K=0.5) (Figs. 6c and A1b, c) because of the presence of a bedrock obstacle at this location. Also, a greater number of modeled channels are observed in the simulations in which K=1, than in the simulation in which K<1 (Fig. 7). This may be due to the fact that, when K=1, new temporary subglacial channels are created due to higher water pressure in the distributed system (Hewitt, 2011). It is worth highlighting that we are able to observe these two phenomena even without the representation of the distributed drainage system in the model.
The volumes of water may be underestimated in the model. Indeed we did not take into account water stored in the snowpack and in the firn layer during the winter–spring period, which is then released during the melt season, nor subglacial meltwater produced at the glacier bed due to geothermal flux and melting of the subglacial channel walls due to the heat transfer induced by the water circulating within the conduits. Despite these simplifications in our estimations of water volumes, since surface meltwater is by far the most important source of water recharge in the subglacial system and that precipitation water is included in our model, we can assume that any water sources that are not taken into account in our study can be neglected (Cogley et al., 2011; Hock, 2005; Irvine-Fynn et al., 2011; Jansson et al., 2003).
The supply of water from surface melt is the most influential runoff component, confirmed by the difference of a factor of 3 in the amount of water provided by melt (72.5 %) and precipitation (27.5 %) during the 2015 melt season for Hansbreen and Werenskioldbreen.
We can conclude that changes in the supraglacial drainage system on a decadal timescale resulted in adjustments of the subglacial drainage system in response to the activation or deactivation of WIAs. Nevertheless, regarding our two study glaciers, the locations of WIAs undergo some change (about 300 m) but generally stay on the same subglacial axes which does not result in a fundamental reorganization of the subglacial system. On an annual timescale, the superficial drainage system of both glaciers remains spatially consistent, implying similar subglacial drainage systems.
The theoretical pattern of subglacial channels under water pressure conditions, ranging from atmospheric to ice overburden, was modeled taking into account local meltwater and precipitation and forcing water penetration inside the glacier thanks to identifying the locations of WIAs for the 2015 melt season.
It can be concluded that considering discrete water recharge makes it impossible to form subglacial channels in most of the accumulation area formed by surface water supply, which is consistent with previous theoretical studies (Fountain and Walder, 1998; Lliboutry, 1971). Concerning Svalbard tidewater glaciers, which have large crevassed areas, modeled patterns of theoretical subglacial channels assuming a spatial water recharge display some imprecisions but are far from being incorrect, especially for the ablation zone. The same may be true for extensively crevassed glaciers during the active phase of a surge. On the contrary, it is important to consider a discrete water recharge for Svalbard land-terminating glaciers with limited crevassed areas (which is mainly the case in this type of glacier). This may be also true for long flat Svalbard tidewater glaciers or even glaciers in a quiescent phase of a surge. In any case, considering a discrete water recharge when modeling patterns of theoretical subglacial channels makes it possible to achieve more realistic results.
Changes in the location of subglacial channels depend to a great extent on changes at the surface (topography and supraglacial drainage system). The permanency of the supraglacial drainage system from year to year and the lack of major changes on a decadal timescale allow us to consider our subglacial channels models to be valid, maybe with some slight changes, for a minimum period of 20 years.
This paper presents a new way of modeling the pattern of subglacial conduits of glaciers. It includes a discrete water recharge, based on a precise mapping of the entire glacier surface, and the volume of water runoff specific to all observed WIAs. Consequently, it produces more realistic results than was previously possible. Our model results are validated by observed locations of the outflows of subglacial channels at the front of our two studied cases. A more accurate reconstruction of the routes of subglacial water flow would require a model including englacial water transport and storage, drainage through a subglacial water sheet (distributed drainage system) and subsurface groundwater flow. Our model also needs to be compared with a greater amount of field data, such as dye-tracing measurements and surveys of water discharge from several supraglacial streams sustaining moulins and of glacier outflows.
Data sets are available upon request by contacting Léo Decaux (leodecaux@gmail.com).

Figure A1Map of the theoretical pattern of subglacial channels of Hansbreen modeled with scenarios (1) – K=0.75 (a), K=0.5 (b), K=0.25 (c) – and (2) – K=0.75 (d), K=0.5 (e), K=0.25 (f). The map background is a WorldView-2 VHRS image acquired on 21 August 2015.
LD structured the paper and wrote the main part of the manuscript, created the DEMs of both glaciers, mapped the supraglacial system of both glaciers for the year 2015, determined the WIAs and calculated their catchments and the water input of the model. JJ and MG suggested the subject of study and contributed to the design of the paper. MG also conducted the subglacial water flow simulations. DI was responsible for the ablation and precipitation calculations and data acquisition. All authors contributed to the interpretation of results and the commenting, reviewing and editing of the paper.
The authors declare that they have no conflict of interest.
The authors would like to thank the European Space Agency for providing the
WorldView-2 high-resolution satellite images and SPOT images (project no. C1P.34101
and no. C1P.9630). Fieldwork was supported by the Polish Ministry
of Science and Higher Education (IPY/269/2006). Glaciological, hydrological
and meteorological data were processed by the University of Silesia data
repository within project Integrated Arctic Observing System (INTAROS). This
project has received funding from the European Union's Horizon 2020
research and innovation programme under grant agreement no. 727890. We wish to
thank colleagues from the Polish Polar Station at Hornsund and Dariusz Puczko
from the Institute of Geophysics Polish Academy of Sciences for hospitality
and logistic support during field missions. Access to the meteorological data
from the Hornsund station provided by the Institute of Geophysics, Polish
Academy of Sciences is kindly acknowledged. The advanced stage of this work
and preparation for publication was financed by the Centre for Polar Studies,
University of Silesia – the Leading National Research Centre (KNOW) in Earth
Sciences (2014–2018), No. 03/KNOW2/2014. We also thank Doug Benn and two
anonymous reviewers for reviews that improved the quality of the manuscript,
as well as the editor Olaf Eisen for his patience.
Edited by: Olaf Eisen
Reviewed by: Doug Benn and two anonymous referees
Arnold, N., Richards, K., Willis, I., and Sharp, M.: Initial results from a distributed, physically based model of glacier hydrology, Hydrol. Process., 12, 191–219, 1998. a
Baranowski, S.: The origin of fluted moraine at the fronts of contemporary glaciers, Geograf. Ann. A, 52, 68–75, 1970. a
Baranowski, S.: The subpolar glaciers of Spitsbergen seen against the climate of this region, Wydawnictwa Uniwersytetu wroclawskiego, Wroclaw University Press, Wroclaw, 1977. a
Bartholomew, I., Nienow, P., Sole, A., Mair, D., Cowton, T., Palmer, S., and Wadham, J.: Supraglacial forcing of subglacial drainage in the ablation zone of the Greenland ice sheet, Geophys. Res. Lett., 38, L08502, https://doi.org/10.1029/2011GL047063, 2011. a
Bartholomew, I., Nienow, P., Sole, A., Mair, D., Cowton, T., and King, M. A.: Short-term variability in Greenland Ice Sheet motion forced by time-varying meltwater drainage: Implications for the relationship between subglacial drainage system behavior and ice velocity, J. Geophys. Res.-Earth, 117, F03002, https://doi.org/10.1029/2011JF002220, 2012. a
Benn, D. I., Gulley, J., Luckman, A., Adamek, A., and Glowacki, P. S.: Englacial drainage systems formed by hydrologically driven crevasse propagation, J. Glaciol., 55, 513–523, 2009. a, b, c
Benn, D. I., Thompson, S., Gulley, J., Mertes, J., Luckman, A., and Nicholson, L.: Structure and evolution of the drainage system of a Himalayan debris-covered glacier, and its relationship with patterns of mass loss, The Cryosphere, 11, 2247–2264, https://doi.org/10.5194/tc-11-2247-2017, 2017. a, b
Błaszczyk, M., Jania, J. A., and Hagen, J. O.: Tidewater glaciers of Svalbard: Recent changes and estimates of calving fluxes, Pol. Polar Res., 30, 85–142, 2009. a, b
Błaszczyk, M., Jania, J. A., and Kolondra, L.: Fluctuations of tidewater glaciers in Hornsund Fjord (Southern Svalbard) since the beginning of the 20th century, Pol. Polar Res., 34, 327–352, 2013. a
Błaszczyk, M., Ignatiuk, D., Uszczyk, Cielecka, K., Grabiec, M., Jania, J., Moskalik, M., and Walczowski, W.: Freshwater input to the Arctic fjord Hornsund (Svalbard), Pol. Polar Res., in press, 2019. a
Catania, G. and Neumann, T.: Persistent englacial drainage features in the Greenland Ice Sheet, Geophys. Res. Lett., 37, L02501, https://doi.org/10.1029/2009GL041108 2010. a
Cogley, J. G., Hock, R., Rasmussen, L. A., Arendt, A. A., Bauder, A., Braithwaite, R. J., Jansson, P., Kaser, G., Möller, M., Nicholson, L., and Zemp, M.: Glossary of glacier mass balance and related terms, IHP-VII technical documents in hydrology No. 86, IACS Contribution No. 2, UNESCO-IHP, Paris, available at: http://unesdoc.unesco.org/images/0019/001925/192525e.pdf (last access: February 2019), 2011. a
DeConto, R. M. and Pollard, D.: Contribution of Antarctica to past and future sea-level rise, Nature, 531, 591–597, 2016. a
Fischer, U. H., Braun, A., Bauder, A., and Flowers, G. E.: Changes in geometry and subglacial drainage derived from digital elevation models: Unteraargletscher, Switzerland, 1927–97, Ann. Glaciol., 40, 20–24, 2005. a, b, c
Flowers, G. E. and Clarke, G. K.: Surface and bed topography of Trapridge Glacier, Yukon Territory, Canada: digital elevation models and derived hydraulic geometry, J. Glaciol., 45, 165–174, 1999. a, b
Flowers, G. E. and Clarke, G. K.: A multicomponent coupled model of glacier hydrology 1. Theory and synthetic examples, J. Geophys. Res.-Sol. Ea., 107, 2287, https://doi.org/10.1029/2001JB001122, 2002. a, b
Fountain, A. G. and Walder, J. S.: Water flow through temperate glaciers, Rev. Geophys., 36, 299–328, 1998. a, b, c
Gajek, G., Jania, J., Harasimiuk, M., Grabiec, M., Puczko, D., and Zagórski, P.: Importance of topographic and geologic conditions for behaviour of Spitsbergen glaciers retreating from the sea to land, in: Workshop on the dynamics and mass budget of Arctic glaciers, GLACIODYN (IPY) meeting, 16–19 February 2009, Biogeoscience Institute, University of Calgary, Barrier Lake Station, Kananaskis Country, Alberta, Canada, 16–19, 2009. a
Grabiec, M., Budzik, T., and Głowacki, P.: Modeling and hindcasting of the mass balance of Werenskioldbreen (Southern Svalbard), Arct. Antarct. Alp. Res., 44, 164–179, 2012a. a
Grabiec, M., Jania, J., Puczko, D., Kolondra, L., and Budzik, T.: Surface and bed morphology of Hansbreen, a tidewater glacier in Spitsbergen, Pol. Polar Res., 33, 111–138, 2012b. a, b, c, d
Grabiec, M.: Stan i współczesne zmiany systemów lodowcowych południowego Spitsbergenu w świetle badań metodami radarowymi [The state and contemporary changes of glacial systems in southern Spitsbergen in the light of radar methods], Wydawnictwo Uniwersytetu Śląskiego, Silesia University Press, Silesia, 2017. a, b, c, d, e, f, g, h, i, j, k
Gulley, J.: Structural control of englacial conduits in the temperate Matanuska Glacier, Alaska, USA, J. Glaciol., 55, 681–690, 2009. a
Gulley, J., Benn, D., Müller, D., and Luckman, A.: A cut-and-closure origin for englacial conduits in uncrevassed regions of polythermal glaciers, J. Glaciol., 55, 66–80, 2009. a
Gulley, J., Grabiec, M., Martin, J., Jania, J., Catania, G., and Glowacki, P.: The effect of discrete recharge by moulins and heterogeneity in flow-path efficiency at glacier beds on subglacial hydrology, J. Glaciol., 58, 926–940, 2012. a, b, c
Hagen, J. O., Liestøl, O., Roland, E., and Jørgensen, T.: Glacier atlas of Svalbard and Jan Mayen, Meddelelser nr. 129, Norwegian Polar Institute, Oslo, 1–141, 1993. a
Hagen, J. O., Etzelmüller, B., and Nuttall, A.-M.: Runoff and drainage pattern derived from digital elevation models, Finsterwalderbreen, Svalbard, Ann. Glaciol., 31, 147–152, 2000. a, b
Hagen, J. O., Kohler, J., Melvold, K., and Winther, J.-G.: Glaciers in Svalbard: mass balance, runoff and freshwater flux, Polar Res., 22, 145–159, 2003a. a, b
Hagen, J. O., Melvold, K., Pinglot, F., and Dowdeswell, J. A.: On the net mass balance of the glaciers and ice caps in Svalbard, Norwegian Arctic, Arct. Antarct. Alp. Res., 35, 264–270, 2003b. a
Hanna, E., Huybrechts, P., Steffen, K., Cappelen, J., Huff, R., Shuman, C., Irvine-Fynn, T., Wise, S., and Griffiths, M.: Increased runoff from melt from the Greenland Ice Sheet: a response to global warming, J. Climate, 21, 331–341, 2008. a
Hewitt, I. J.: Modelling distributed and channelized subglacial drainage: the spacing of channels, J. Glaciol., 57, 302–314, 2011. a, b
Hewitt, I. J.: Seasonal changes in ice sheet motion due to melt water lubrication, Earth Planet. Sc. Lett., 371, 16–25, 2013. a
Hock, R.: Glacier melt: a review of processes and their modelling, Prog. Phys. Geogr., 29, 362–391, 2005. a
Hodgkins, R.: Glacier hydrology in Svalbard, Norwegian High Arctic, Quaternary Sci. Rev., 16, 957–974, 1997. a
Hodson, A., Gurnell, A., Washington, R., Tranter, M., Clark, M., and Hagen, J.: Meteorological and runoff time-series characteristics in a small, High-Arctic glaciated basin, Svalbard, Hydrol. Process., 12, 509–526, 1998. a
Hoffman, M., Catania, G., Neumann, T., Andrews, L., and Rumrill, J.: Links between acceleration, melting, and supraglacial lake drainage of the western Greenland Ice Sheet, J. Geophys. Res.-Earth, 116, F04035, https://doi.org/10.1029/2010JF001934, 2011. a
Holmlund, P.: Internal geometry and evolution of moulins, Storglaciären, Sweden, J. Glaciol., 34, 242–248, 1988. a, b
How, P., Benn, D. I., Hulton, N. R. J., Hubbard, B., Luckman, A., Sevestre, H., van Pelt, W. J. J., Lindbäck, K., Kohler, J., and Boot, W.: Rapidly changing subglacial hydrological pathways at a tidewater glacier revealed through simultaneous observations of water pressure, supraglacial lakes, meltwater plumes and surface velocities, The Cryosphere, 11, 2691–2710, https://doi.org/10.5194/tc-11-2691-2017, 2017. a, b
Ignatiuk, D.: Bilans energetyczny powierzchni lodowca a zasilanie system drenażu glacjalnego Werenskioldbreen, PhD thesis, Uniwersytet Slaski, Sosnowiec, 2012. a
Ignatiuk, D., Piechota, A., Ciepły, M., and Luks, B.: Changes of altitudinal zones of Werenskioldbreen and Hansbreen in period 1990–2008, Svalbard, in: vol. 1618, AIP Conference Proceedings, 4–7 April 2014, Athens, Greece, 275–280, 2014. a, b, c
Irvine-Fynn, T. D., Hodson, A. J., Moorman, B. J., Vatne, G., and Hubbard, A. L.: Polythermal glacier hydrology: A review, Rev. Geophys., 49, RG4002, https://doi.org/10.1029/2010RG000350, 2011. a, b, c
Jansson, P., Hock, R., and Schneider, T.: The concept of glacier storage: a review, J. Hydrol., 282, 116–129, 2003. a
Kessler, M. A. and Anderson, R. S.: Testing a numerical glacial hydrological model using spring speed-up events and outburst floods, Geophys. Res. Lett., 31, L18503, https://doi.org/10.1029/2004GL020622, 2004. a
Larsen, C. F., Motyka, R. J., Arendt, A. A., Echelmeyer, K. A., and Geissler, P. E.: Glacier changes in southeast Alaska and northwest British Columbia and contribution to sea level rise, J. Geophys. Res.-Earth, 112, F01007, https://doi.org/10.1029/2006JF000586, 2007. a
Lliboutry, L.: Permeability, brine content and temperature of temperate ice, J. Glaciol., 10, 15–29, 1971. a, b, c
Mair, D., Nienow, P., Sharp, M., Wohlleben, T., and Willis, I.: Influence of subglacial drainage system evolution on glacier surface motion: Haut Glacier d'Arolla, Switzerland, J. Geophys. Res.-Sol. Ea., 107, 2175, https://doi.org/10.1029/2001JB000514, 2002. a
Majchrowska, E., Ignatiuk, D., Jania, J., Marszałek, H., and Wąsik, M.: Seasonal and interannual variability in runoff from the Werenskioldbreen catchment, Spitsbergen, Pol. Polar Res., 36, 197–224, 2015. a, b, c, d, e, f
Mankoff, K. D., Gulley, J. D., Tulaczyk, S. M., Covington, M. D., Liu, X., Chen, Y., Benn, D. I., and Głowacki, P. S.: Roughness of a subglacial conduit under Hansbreen, Svalbard, J. Glaciol., 63, 423–435, 2017. a
Mavlyudov, B. R.: Internal drainage systems of glaciers, Institute of geography RAS, Inst. of Geogr., Russ. Acad. of Sci., Moscow, p. 396, 2006. a
Moon, T. and Joughin, I.: Changes in ice front position on Greenland's outlet glaciers from 1992 to 2007, J. Geophys. Res.-Earth, 113, F02022, https://doi.org/10.1029/2007JF000927, 2008. a
Murray, T., Benn, D., Maghami-Nick, F., and Adamek, A.: Mapping the course of an englacial channel using ground-penetrating radar at Hansbreen, Svalbard, in: AGU Fall Meeting Abstracts, 10–14 December 2007, San Francisco, USA, 2007. a, b
Navarro, F., Martín-Español, A., Lapazaran, J., Grabiec, M., Otero, J., Vasilenko, E., and Puczko, D.: Ice volume estimates from ground-penetrating radar surveys, Wedel Jarlsberg Land glaciers, Svalbard, Arct. Antarct. Alp. Res., 46, 394–406, 2014. a, b
Nienow, P. and Hubbard, B.: Surface and englacial drainage of glaciers and ice sheets, in: Encyclopedia of Hydrological Sciences, John Wiley & Sons, London, 2006. a, b, c
Nienow, P., Sharp, M., and Willis, I.: Seasonal changes in the morphology of the subglacial drainage system, Haut Glacier d'Arolla, Switzerland, Earth Surf. Proc. Land., 23, 825–843, 1998. a
Nowak, A. and Hodson, A.: Hydrological response of a High-Arctic catchment to changing climate over the past 35 years: a case study of Bayelva watershed, Svalbard, Polar Res., 32, 19691, https://doi.org/10.3402/polar.v32i0.19691, 2013. a, b
Nuth, C., Moholdt, G., Kohler, J., Hagen, J. O., and Kääb, A.: Svalbard glacier elevation changes and contribution to sea level rise, J. Geophys. Res.-Earth, 115, F01008, https://doi.org/10.1029/2008JF001223, 2010. a
Nye, J. F.: The flow law of ice from measurements in glacier tunnels, laboratory experiments and the Jungfraufirn borehole experiment, P. Roy. Soc. Lond. A, 219, 477–489, 1953. a
Pachauri, R. K., Allen, M. R., Barros, V. R., Broome, J., Cramer, W., Christ, R., Church, J. A., Clarke, L., Dahe, Q., Dasgupta, P., and Dubash, N. K.: Climate change 2014: synthesis report, in: Contribution of Working Groups I, II and III to the fifth assessment report of the Intergovernmental Panel on Climate Change, IPCC, Geneva, Switzerland, 2014. a
Pälli, A., Moore, J. C., Jania, J., Kolondra, L., and Glowacki, P.: The drainage pattern of Hansbreen and Werenskioldbreen, two polythermal glaciers in Svalbard, Polar Res., 22, 355–371, 2003. a, b, c, d, e, f, g, h, i, j, k, l
Paterson, W.: The physics of glaciers, Pergamon Press, Oxford, UK, 480 pp., 1994. a
Poinar, K., Joughin, I., Das, S. B., Behn, M. D., Lenaerts, J., and Broeke, M. R.: Limits to future expansion of surface-melt-enhanced ice flow into the interior of western Greenland, Geophys. Res. Lett., 42, 1800–1807, 2015. a, b
Price, S. F., Payne, A. J., Howat, I. M., and Smith, B. E.: Committed sea-level rise for the next century from Greenland ice sheet dynamics during the past decade, P. Natl. Acad. Sci. USA, 108, 8978–8983, 2011. a
Pulina, M., Kolondra, L., and Řehák, J.: Charting of cryokarst forms on Werenskiold Glacier (SW Spitsbergen), in: XXVI Polar Symposium, Lublin, Polish Polar Studies, 18–20 June 1999, Lublin, Poland, 235–241, 1999. a
Rignot, E., Velicogna, I., van den Broeke, M. R., Monaghan, A., and Lenaerts, J. T.: Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise, Geophys. Res. Lett., 38, L05503, https://doi.org/10.1029/2011GL046583, 2011. a
Röthlisberger, H.: Water pressure in intra-and subglacial channels, J. Glaciol., 11, 177–203, 1972. a, b
Ryser, C., Lüthi, M., Blindow, N., Suckro, S., Funk, M., and Bauder, A.: Cold ice in the ablation zone: Its relation to glacier hydrology and ice water content, J. Geophys. Res.-Earth, 118, 693–705, 2013. a, b
Schroeder, J.: Hans glacier moulins observed from 1988 to 1992, Svalbard, Norweg. J. Geogr., 52, 79–88, https://doi.org/10.1080/00291959808552387, 1998. a, b, c
Sharp, M., Richards, K., Willis, I., Arnold, N., Nienow, P., Lawson, W., and Tison, J.-L.: Geometry, bed topography and drainage system structure of the Haut Glacier d'Arolla, Switzerland, Earth Surf. Proc. Land., 18, 557–571, 1993. a, b, c
Shepherd, A., Hubbard, A., Nienow, P., King, M., McMillan, M., and Joughin, I.: Greenland ice sheet motion coupled with daily melting in late summer, Geophys. Res. Lett., 36, L01501, https://doi.org/10.1029/2008GL035758, 2009. a
Shreve, R.: Movement of water in glaciers, J. Glaciol., 11, 205–214, 1972. a, b, c
Smith, L. C., Chu, V. W., Yang, K., Gleason, C. J., Pitcher, L. H., Rennermalm, A. K., Legleiter, C. J., Behar, A. E., Overstreet, B. T., Moustafa, S. E., and Tedesco, M.: Efficient meltwater drainage through supraglacial streams and rivers on the southwest Greenland ice sheet, P. Natl. Acad. Sci. USA, 112, 1001–1006, 2015. a, b
Sundal, A. V., Shepherd, A., Nienow, P., Hanna, E., Palmer, S., and Huybrechts, P.: Melt-induced speed-up of Greenland ice sheet offset by efficient subglacial drainage, Nature, 469, 521–524, 2011. a
Turu, V.: Surface NMR survey on Hansbreen Glacier, Hornsund, SW Spitsbergen (Norway), Landform Analysis, 21, 57–74, 2012. a, b
Van der Veen, C. J.: Fracture propagation as means of rapidly transferring surface meltwater to the base of glaciers, Geophys. Res. Lett., 34, L01501, https://doi.org/10.1029/2006GL028385, 2007. a, b
Vieli, A., Jania, J., Blatter, H., and Funk, M.: Short-term velocity variations on Hansbreen, a tidewater glacier in Spitsbergen, J. Glaciol., 50, 389–398, 2004. a
Werder, M. A., Hewitt, I. J., Schoof, C. G., and Flowers, G. E.: Modeling channelized and distributed subglacial drainage in two dimensions, J. Geophys. Res.-Earth, 118, 2140–2158, 2013. a
WGMS: Fluctuations of Glaciers Database, World Glacier Monitoring Service, Zurich, Switzerland, https://doi.org/10.5904/wgms-fog-2017-10, 2017. a
Willis, I., Lawson, W., Owens, I., Jacobel, B., and Autridge, J.: Subglacial drainage system structure and morphology of Brewster Glacier, New Zealand, Hydrol. Process., 23, 384–396, 2009. a
Yang, K. and Smith, L. C.: Supraglacial streams on the Greenland Ice Sheet delineated from combined spectral–shape information in high-resolution satellite imagery, IEEE Geosci. Remote Sens. Lett., 10, 801–805, 2013. a