the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Western Greenland ice sheet retreat history reveals elevated precipitation during the Holocene thermal maximum
Jacob Downs
Jesse Johnson
Jason Briner
Nicolás Young
Alia Lesnek
Josh Cuzzone
We investigate changing precipitation patterns in the Kangerlussuaq region of western central Greenland during the Holocene thermal maximum (HTM), using a new chronology of ice sheet terminus position through the Holocene and a novel inverse modeling approach based on the unscented transform (UT). The UT is applied to estimate changes in annual precipitation in order to reduce the misfit between modeled and observed terminus positions. We demonstrate the effectiveness of the UT for time-dependent data assimilation, highlighting its low computational cost and trivial parallel implementation. Our results indicate that Holocene warming coincided with elevated precipitation, without which modeled retreat in the Kangerlussuaq region is more rapid than suggested by observations. Less conclusive is whether high temperatures during the HTM were specifically associated with a transient increase in precipitation, as the results depend on the assumed temperature history. Our results highlight the important role that changing precipitation patterns had in controlling ice sheet extent during the Holocene.
During the early Holocene (∼11.7–8 ka), terrestrial and marine climate proxies from the Northern Hemisphere reveal a warmer than present peak in temperature (Kaufman et al., 2004; Marcott et al., 2013). This period of elevated temperatures, likely initiated by greater than modern insolation, is referred to as the Holocene thermal maximum (HTM). Its onset, duration, and severity were likely spatially variable (Kaufman et al., 2004). Records of HTM warming can be found in Greenland ice core records. For example, temperatures measured in the Dye-3 borehole show a pronounced HTM signal occurring from 7 to 4 ka and having values 2.5∘C above present temperatures (Dahl-Jensen et al., 1998; Miller et al., 2010), whereas at the GISP2 site, the HTM appears to occur slightly earlier, following the 8.2 ka cold event (Kobashi et al., 2017) (Fig. 1).
While warming during the HTM is well established, less is known about the regional changes in precipitation that accompanied increased temperatures. Ice core records provide long-term estimates of accumulation (Alley et al., 1993), but these point measurements near ice divides are not representative of the precipitation across the ice sheet, particularly at lower elevations near the coast. Because the HTM was accompanied by lower Arctic sea ice extent (Polyak et al., 2010), it is possible that additional moisture was available to the Greenland ice sheet (GrIS) from open Arctic waters. This is supported by proxy evidence showing an increase in winter precipitation in western Greenland coincident with HTM warming (Thomas et al., 2016). However, temperature is known with greater certainty than precipitation.
Understanding feedbacks between temperature and precipitation during the HTM has implications for the future of the GrIS. Warming and declining sea ice are projected to cause an increase in Arctic precipitation (Bintanja and Selten, 2014; Singarayer et al., 2006). On a global scale, the moisture content of the atmosphere increases by around 7 % for every degree of warming, according to the Clausius–Clapeyron relation. On a regional scale, declining Arctic sea ice is expected to cause changes in atmospheric circulation, bringing more moisture to the Arctic (Bintanja and Selten, 2014). While there are important differences between HTM and modern climate, the history of retreat in western Greenland may provide insights into how the GrIS will respond to a warmer and possibly wetter future climate.
Modeling studies indicate that Holocene retreat in land-terminating regions of the GrIS were controlled primarily by surface mass balance rather than ice dynamics (Cuzzone et al., 2019; Lecavalier et al., 2014). Given the primary importance of surface mass balance in controlling modeled retreat, we explore the hypothesis that enhanced winter snowfall during the HTM may have slowed retreat by partially offsetting increased surface melt (Thomas et al., 2016). We investigate changes in precipitation in a land-terminating sector of the western central GrIS, near Kangerlussuaq, taking advantage of a new chronology of ice sheet terminus position (Young et al., 2020) and a novel inverse modeling approach based on the unscented transform (UT) (Julier and Uhlmann, 1997). In particular, we use the UT to estimate changes in annual precipitation during the Holocene by reducing the misfit between modeled and observed terminus positions in an isothermal flow line ice dynamics model (Brinkerhoff et al., 2017) (Sect. 2.1).
The inverse problem is posed as a Bayesian inference problem, and its solution involves estimating a non-Gaussian posterior probability distribution. Markov chain Monte Carlo (MCMC) methods, such as the Metropolis–Hastings method (Chib and Greenberg, 1995), provide one means of solving the inference problem by generating random samples from the posterior distribution. Generating samples from the posterior, however, requires repeatedly running the ice dynamics model with different precipitation histories as input, which is intractable even for a relatively computationally inexpensive flow line model.
The unscented transform provides a computationally efficient and trivially parallelizable alternative to MCMC methods. The basic idea of the unscented transform is to use a small, fixed number of deterministic sample points in order to estimate the statistical moments (e.g., mean and covariance) of the posterior distribution. Sigma points, each of which represents a different precipitation history input to the ice dynamics model, are generated a priori (Sect. 2.5.3). Consequently, all model runs can be performed simultaneously in parallel resulting in at least a 100-fold speed-up compared to MCMC methods.
2.1 Ice sheet model
We use the 1D isothermal flow line model with higher-order momentum balance described in Brinkerhoff et al. (2017). The momentum conservation equations are simplified using the Blatter–Pattyn approximation, assuming hydrostatic pressure and negligible vertical resistive stresses (Blatter, 1995; Pattyn, 2003). Default parameter values used in this work are specified in Table 1.
We adopt a linear sliding law of the form
where τb is basal shear stress, β2 is a constant basal traction parameter, N is effective pressure, and ub is sliding speed. Based on borehole water pressure measurements in Wright et al. (2016), basal water pressure Pw is assumed to be a fixed fraction Pfrac=0.85 of ice overburden pressure P0. Effective pressure is therefore given by
The basal traction parameter β2 is tuned to minimize the misfit between modeled and observed surface velocities from Mouginot et al. (2017) for present-day Isunnguata Sermia values.
2.2 Flow line selection and moraine age constraints
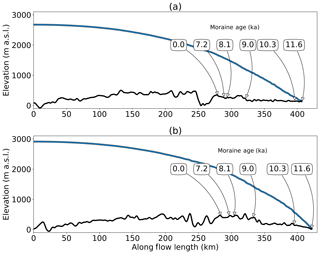
To define the path followed by ice, we assume that flow follows the modern surface velocity field inland of the present-day margin. In ice-free regions, the direction of ice flow is inferred from bedrock topography (Fig. 1). Since the direction of ice flow is unknown and time varying, we cannot directly quantify the uncertainty introduced by errors in flow line selection. To account for some of this uncertainty, we perform inversions on two plausible adjacent paleo-flow lines in the Kangerlussuaq area.
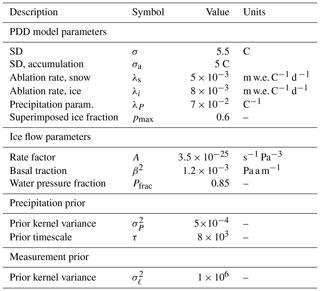
The rate of Holocene retreat on each flow line is estimated using constraints on ice sheet terminus position from (Young et al., 2020) (Fig. 1). Terminus position data in Young et al. (2020) indicate that in the early Holocene (11.6 ka), the ice sheet margin was tens of kilometers inland of the present-day coastline. Although the moraine patterns are spatially complex, generally speaking there was a period of moderate retreat (∼10 km on the northern flow line and ∼30 km on the southern flow line) from 11.6 to 10.3 ka, followed by rapid retreat (∼100 km on both flow lines) from 10.3 to 8.1 ka. By 8.1 ka, the margin position was within 20 km of its present position on both flow lines (Fig. 5). The modern terminus position provides one additional constraint. Moraine ages have uncertainties of up to ±400 years.
For modern bedrock geometry along the flow lines, we use BedMachine v3 (Morlighem et al., 2017). Isostatic uplift and relative sea level changes are accounted for using a glacial isostatic adjustment model (Caron et al., 2018). This model, combined with the retreat chronology in Young et al. (2020), indicates that ice remained grounded on both the northern and southern flow lines from 11.6 ka onward.
2.3 Positive degree day model
Surface mass balance is estimated using a positive degree day (PDD) model (Johannesson et al., 1995). Annual surface mass balance is constructed in the PDD model using estimates of average monthly precipitation and temperature. Inputs into the PDD model include the unknown ice surface elevation S, modern monthly temperature Tm and precipitation Pm along the flow lines, as well as the seasonal temperature anomaly ΔT. As in Cuzzone et al. (2019), modern temperature and precipitation are computed as 30-year averages from 1980 to 2010 using the method of Box (2013).
To assess the sensitivity of modeled retreat history to temperature, we perform experiments using temperature reconstructions from both Buizert et al. (2018) and Dahl-Jensen et al. (1998). For the spatially explicit Buizert et al. (2018) reconstruction, monthly temperature anomalies are computed as averages along the flow lines. In contrast, Dahl-Jensen et al. (1998) reconstruct temperature only at the GRIP and Dye-3 borehole locations (Fig. 1). Since a full Holocene reconstruction is unavailable at the Dye-3 borehole site, which is closer to Kangerlussuaq, we use the temperature reconstruction at GRIP. The HTM is roughly 0.3 ∘C warmer and 1500 years later in Dahl-Jensen et al. (1998) than in Buizert et al. (2018) (Fig. 6).
A limitation of the Dahl-Jensen et al. (1998) reconstruction is that it does not resolve seasonal temperatures. To address this, we calculate the difference between monthly and mean annual temperatures in Buizert et al. (2018) and apply those offsets to the mean annual temperature at GRIP from Dahl-Jensen et al. (1998).
Surface temperature T is computed monthly as
where Sm is the modern surface elevation and α= 5∘C km−1 is the lapse rate (Abe-Ouchi et al., 2007). Following Ritz et al. (2001) and Cuzzone et al. (2019), precipitation P along the flow line is estimated based on the Clausius–Clapeyron relation. In particular, precipitation is estimated by
The term PT accounts for changes in precipitation solely due to changes in temperature. Here λP=0.07, which results in a 7 % increase in precipitation for every 1 ∘C increase in temperature above modern (Abe-Ouchi et al., 2007; Ritz et al., 2001).
The term PT does not capture the effects of many unknown climate factors that may have caused dynamic regional changes in Holocene precipitation. Therefore, we introduce a precipitation anomaly term ΔP, analogous to the temperature anomaly ΔT. This time-dependent function, which has units of meters water equivalent per annum (m w.e. a−1), is used to adjust precipitation uniformly across a flow line in order to reduce mismatch between modeled and observed terminus positions. Unlike ΔT, which can be inferred from ice cores, ΔP will be used as a control variable to be determined using the inverse methods detailed in Sect. 2.5.3. Equations (3) and (4) provide a method of accounting for elevation changes through time and downscaling inputs to match the mesh resolution of the model (∼1 km).
Positive degree days and snowfall are computed month by month based on mean monthly temperature and precipitation (Johannesson et al., 1995). Snow is melted first at a rate of m w.e. ∘ d−1 followed by ice at a rate of m w.e. ∘ d−1. Snow melt is initially supposed to refreeze in the snowpack as superimposed ice. Runoff begins when the superimposed ice reaches a given fraction (60 %) of the snow cover (Reeh, 1991). A listing of ice flow and PDD model parameters is provided in Table 1, and all data sets used in the model are shown in Table 2.
2.4 Modeling limitations
A limitation of our modeling approach is that we do not account for potential ice dynamical effects caused by changes in surface runoff or subglacial hydrology. Modeling melt water runoff would be difficult in a flow line model due to flux of melt water in and out of the path of ice flow. Another limitation is that our model is isothermal. Unless ice temperature is treated in a vertically averaged sense, resolving temperature would require a 2D mesh, which would considerably increase the computational cost of the model. We consider the consequences of this simplification in Sect. 3.3, where we test sensitivity to the ice hardness parameter.
The PDD scheme outlined in Sect. 2.3 does not account for changes in surface mass balance due to orographic forcing or other complex interactions between the ice sheet and climate system that could be captured by coupling the ice sheet model to an Earth system model (Bahadory and Tarasov, 2018). Since our emphasis is on estimating precipitation and surface mass balance using an inverse modeling approach, we believe the computational cost of such an approach outweighs the benefits. Uncertainties related to feedbacks between ice dynamics and climate are assessed via extensive sensitivity testing (Sect. 3.3).
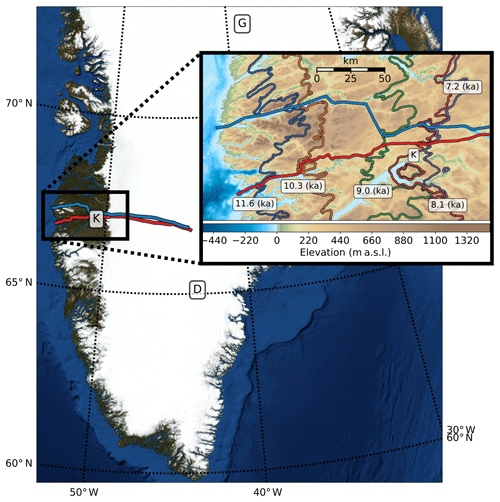
Figure 1K marks the position of Kangerlussuaq, while D and G mark the locations of the Dye-3 and GISP2 boreholes, respectively. Northern and southern paleo-flow lines are shown as blue and red lines running left to right. The inset shows a detailed view of the modeled region. Modern bedrock elevation is expressed in meters above sea level. Historical moraines dating from 11.6 to 7.2 ka are indicated by labeled lines.
2.5 Data assimilation approach
In order to assess the initial mismatch between modeled and observed retreat histories, we perform a reference experiment with ΔP=0 and ΔT estimates from both Buizert et al. (2018) and Dahl-Jensen et al. (1998). To improve the fit to observations, we assimilate terminus position data to obtain improved estimates of Holocene precipitation anomalies. Previous modeling studies indicate that Holocene retreat in land-terminating sectors of the GrIS were dominated by surface mass balance rather than ice dynamics (Cuzzone et al., 2019; Lecavalier et al., 2014). Uncertainty in Holocene climate, and consequently surface mass balance, is therefore likely the primary cause of discrepancies between modeled and observed terminus positions.
In principle, ΔP, ΔT, or both could be tuned to improve the fit between modeled and observed terminus positions. We focus on precipitation because it is more poorly constrained than temperature. In the upcoming sections, we introduce a framework for time-dependent data assimilation based on the unscented transform (UT). Sections 2.5.1–2.5.2 outline the basic tenets of the UT. Sections 2.5.3–2.5.7 outline how the UT can be applied to estimate precipitation anomalies.
2.5.1 Overview of the unscented transform
In what follows, the notation x∼𝒩(x0, Px) means that x is a normally distributed random variable with mean vector x0 and covariance matrix Px. Suppose that ), and is a nonlinear function. We would like to estimate the distribution of the non-Gaussian random variable
where ) is the measurement noise.
In general, the non-Gaussian probability distribution for y can be approximated using Markov chain Monte Carlo (MCMC) methods such as the Metropolis–Hastings algorithm (Chib and Greenberg, 1995). However, if the nonlinear function is time-consuming to compute, generating thousands of MCMC samples is often intractable. As a computationally efficient alternative to MCMC methods, Julier and Uhlmann (1997) introduced a method for approximating the mean and covariance of y called the unscented transform (UT) 1.
The term unscented transform has been applied somewhat broadly to a family of methods that approximate the statistical moments of a non-Gaussian random variable using a small, deterministic set of sample points called sigma points. It is known primarily in the context of the unscented Kalman filter. However, the UT can be applied more generally as an alternative to traditional MCMC methods. Sigma points and weight sets are designed to accurately estimate moments of a transformed random variable using a minimal number of function evaluations.
A set of vectors, called sigma points, are chosen with the same weighted sample mean and weighted covariance structure as x. There are many algorithms for generating sigma points sets with different numbers of points and orders of accuracy. A commonly used set of 2n+1 sigma points is given by
with corresponding mean and covariance weights given by
The notation refers to the ith row of a matrix square root (typically computed by Cholesky factorization) of Px, and κ is a free parameter controlling the scaling of the sigma points around the mean. Julier and Uhlmann (1997) recommend a default value of . However, κ can be fine-tuned to reduce prediction errors for a given problem.
Young et al. (2020)Morlighem et al. (2017)Mouginot et al. (2017)Box (2013)Buizert et al. (2018)Dahl-Jensen et al. (1998)Caron et al. (2018)The nonlinear function ℱ is applied to each sigma point to yield a set of transformed points
The mean and covariance matrix Py of y are then estimated as weighted sums.
A visual example of this algorithm is shown in Fig. 2.
Figure 2(a) White points are samples from a 2D Gaussian distribution ). The red ellipse represents the covariance of the distribution, while red points are sigma points χi used for the unscented transform (UT). (b) White points are samples from the transformed, non-Gaussian distribution for with ). Red points are transformed sigma points 𝓨i=ℱ(χi). UT approximations of the mean and covariance Py of y are estimated via weighted sums of transformed sigma points.
2.5.2 Bayesian inference using the UT
Given a measurement of yo, we would like to estimate the posterior distribution
Using an approach called statistical linearization (Särkkä, 2013) the joint distribution for [x, y]T can be approximated by
with
Here, 𝓧i and 𝓨i=ℱ(𝓧i) are sigma points and transformed sigma points, respectively. Matrices Py and Pxy are known as the measurement covariance and cross covariance, respectively.
Given a measurement y0, the joint distribution then easily yields a Gaussian approximation of the posterior distribution. Using the following equation:
we have
where x′ and P′ are approximations of the posterior mean and covariance, respectively. Readers familiar with Kalman filters might recognize that x′ and P′ are computed using a Kalman “update” step given a measurement yo and Kalman gain K (Särkkä, 2013).
2.5.3 Assimilating glacier length observations
Time-dependent data assimilation using the UT involves running the ice sheet model with a set of different precipitation anomaly histories, each corresponding to a different sigma point. This is followed by a post-processing step, which incorporates the ice sheet terminus chronology data via a correction of the prior mean vector and covariance matrix. Implementation of the unscented transform is straightforward and easily parallelizable since each model run is independent. In the following section, we outline the mathematical details of this process.
We seek to find ΔP histories that match the observed retreat history on both flow lines. An optimal solution should reproduce the observed retreat history within uncertainty while not overfitting the data. We discretize the problem by estimating the precipitation anomaly at times ranging from 11.6 to 0 ka. In practice, we use a regular grid of 44 points, spaced roughly 250 years apart. Precipitation anomaly values at these time points are denoted by , respectively, and assembled in a vector
Given a multivariate Gaussian prior ), which encodes assumptions about the structure of the precipitation anomaly (Sect. 2.5.4), we would like to estimate the mean and covariance of the posterior distribution
Here, the measurement vector
contains measured glacier lengths at discrete points in time. Our procedure for defining the measurement mean yo and covariance R are discussed in Sect. 2.5.5.
We can think of the ice sheet model as a function that maps precipitation anomaly inputs to glacier length outputs with some additive observation noise
Discrete precipitation anomaly values are linearly interpolated for input into the ice dynamics model, which has time steps on the order of months. The function ℱ returns glacier lengths at the same m discrete times as in ℓ0.
To predict the posterior distribution, we use the methods outlined in Sect. 2.5.1 and 2.5.2. First, sigma points are generated based on the prior distribution for Δp. To reduce computational costs, we use a minimal set of sigma points 𝓟i with corresponding weights generated using the method presented in Menegaz et al. (2011). Their method includes one free parameter , which can be tuned to reduce prediction errors. While this method has a lower order of accuracy than other methods, we find it often produces comparable results to other larger sigma point sets in practice.
Sigma points are propagated through the model to obtain transformed points 𝓛i=ℱ(𝓟i). In this context, sigma points 𝓟i correspond to different time-dependent precipitation anomaly histories, while the transformed points 𝓛i correspond to the resulting glacier length histories when those precipitation anomalies are used as inputs (Fig. 3). The structure of the sigma points reflects the mathematical formulation of the Menegaz et al. (2011) sigma points. Hence, they are not merely random samples from the prior distribution.
Transformed sigma points are computed simultaneously in parallel, using one core per sigma point. After all transformed sigma points have been computed, the mean and covariance of the posterior distribution are estimated as outlined in Sect. 2.5.2. In parallel, this procedure takes roughly the same amount of time as a single forward model run. Unlike a standard filtering approach to data assimilation, all measurement data are incorporated simultaneously rather than time step by time step. For that reason, the Kalman update step corrects the entire time-dependent precipitation history at once. Moreover, unlike in Kalman smoothing, we approximate the full posterior distribution rather than the probability distributions
Note that the variables Δpk with k≠i are marginalized out of the Kalman smoothing distributions. The use of time-dependent sigma points distinguishes our approach from standard Kalman filtering or Kalman smoothing approaches, and does not rely on the assumptions that states (Δpi) and measurements (ℓi) satisfy the Markov property.
2.5.4 Gaussian process prior for regularization
We adopt a Gaussian process prior (Rasmussen, 2004) to control the temporal smoothness of ΔP. A Gaussian process can be thought of as a distribution over functions. That is, random samples from a Gaussian process are functions rather than individual points or vectors. A collection of random variables is said to be drawn from a Gaussian process with mean function m(⋅) and covariance function ) if, for any finite set of elements , the random variables ) have the distribution
with
and
The set 𝒯 is called the index set, and specifies the domain of the Gaussian process. Here, the index set represents points in time.
The prior distribution for Δp has mean vector Δp0 and covariance matrix P0=K of the form shown in Eq. (27). We use a squared exponential covariance function
where σ2 is a scaling constant and τ is a characteristic timescale. Variables Δpi and Δpk are more highly correlated the closer they are in time. In effect, this acts as a form of temporal regularization, in which smooth precipitation history functions are preferred over less smooth ones. We discuss the choice of the mean Δp0 in Sect. 3.2.
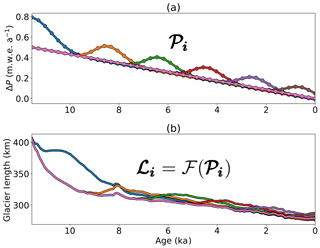
Figure 3(a) A subset of 6 out of a total of 45 Menegaz et al. (2011) sigma points 𝓟i representing different precipitation anomaly histories. (b) Six corresponding glacier length histories 𝓛i or transformed sigma points obtained by inputting the sigma points 𝓟i into the ice dynamics model ℱ.
2.5.5 Measurement mean and variance
Observations of terminus position are available roughly every 1000 years between 11.6 and 7.2 ka, with a gap from 7.2 ka to present. In contrast, model time steps are on the order of months. Due to these disparate timescales, we use the following procedure to estimate the measurement mean ℓ0 and covariance matrix R on a timescale more appropriate for the ice sheet model.
We define a Gaussian process prior of “candidate” glacier length histories ℓP(t) as follows. The mean function ) is obtained by linearly interpolating between glacier length observations. The Brownian covariance kernel for the Gaussian process is defined by
Candidate retreat histories are generated by drawing random samples from the Gaussian process. The Brownian covariance kernel results in random glacier length histories that are somewhat noisy but correlated over shorter timescales (Fig. 4). Candidate length histories are resampled so that the mean moraine formation times and uncertainties match the observations in Young et al. (2020). Hence, highly implausible candidate histories are rejected. The average length and variance of this culled set of samples is computed at a series of time slices to obtain a plausible measurement mean ℓ0 and diagonal measurement covariance matrix R (Fig. 4).
2.5.6 Iterative optimization procedure
Optimizations are conducted in multiple passes. In the first pass, the measurement covariance matrix R is multiplied by a factor of 0.25 so that the measurements are initially weighted more than the prior. This produces a reasonable fit to the data, even given a poor initial estimate of ΔP. The optimal precipitation anomaly from a given iteration is used as the prior mean in the next iteration. We use the same prior covariance matrix P0 for regularization in each iteration. After two to three iterations, modeled and observed terminus positions match within measurement uncertainty (Sect. 3). In our experience, the results of iteration are not dependent on the choice of prior mean in the first iteration, but we find that convergence can be improved by choosing a sensible initial guess, as in Sect. 3.2.
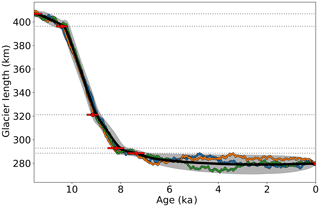
Figure 4The measurement mean ℓ0 (solid black line) and 95 % confidence bands (gray shaded region) for the northern flow line are estimated by generating random retreat histories with the same mean moraine formation ages and variances as the observations. The green, blue, and orange lines represent four random plausible retreat histories. Red dots denote the estimated mean moraine formation ages, while red lines show 95 % confidence intervals.
2.5.7 Approach to sensitivity testing
As described, the data assimilation method accounts for measurement but not model uncertainty. It can easily be extended to account for uncertainties in the ice flow and PDD model parameters. We define an augmented state vector
where θ is a vector of scalar parameters including the natural logarithm of the rate factor for ice, the basal traction parameter, a parameter controlling precipitation scaling with temperature, and the PDD melt rate parameters for ice and snow
The prior distribution for the augmented state vector is given by
where θ0 is the parameter mean vector and Θ is a diagonal matrix containing parameter variances.
The unscented transform is applied to the augmented function
to obtain estimates of the joint distribution for and the conditional distribution for . Since parameters are included as state variables, sigma points reflect a variety of precipitation histories and parameter sets. A model run for a particular sigma point is initialized from an appropriate steady state using the parameter set for that point.
2.6 Model initialization
Model runs are initialized by tuning the precipitation anomaly to obtain a steady state at 12.6 ka, with a margin position 5 km beyond the 11.6 ka moraine. We invert for a precipitation anomaly time series that forces a retreat of 5 km over 1000 years to obtain an initial ice sheet configuration with the correct terminus position at 11.6 ka (Fig. 5). This initialization procedure is intended to ease the ice sheet out of steady state in order to avoid strong transient effects at the beginning of model runs.
3.1 Reference experiment
To assess the initial misfit between modeled and observed Holocene retreat, the model is forced with ΔT reconstructions from Buizert et al. (2018) and Dahl-Jensen et al. (1998) and a zero precipitation anomaly. Precipitation is scaled with temperature according to Eq. (4), neglecting possible influences from changing Arctic sea ice cover, atmospheric circulation, or other unknown climate factors. Modeled ice retreat is far more rapid than observed on both flow lines (Fig. 8). Colder temperatures during the early Holocene (Fig. 8a) lead to a somewhat more plausible retreat history using the Dahl-Jensen et al. (1998) temperature forcing versus the Buizert et al. (2018) forcing. However, by 8 ka, ice has retreated inland of the present-day margin in both reconstructions.
3.2 Precipitation anomaly inversions
We estimate precipitation anomalies on the northern and southern flow lines using both the Buizert et al. (2018) and Dahl-Jensen et al. (1998) temperature reconstructions. Given the rapid retreat in the reference experiment, we expect that a positive precipitation anomaly will be required to match observed terminus positions in the early Holocene. Therefore, in the first round of optimization, we assume a prior mean of the form
where is a rescaled time variable that increases from zero at 11.6 ka to one at 0 ka. The results of the iterative optimization procedure are insensitive to the prior mean selected in the first iteration. Using a sigma point scaling parameter w0=0.5 for the Menegaz et al. (2011) sigma point set ensures that a wide region around the mean is explored in each iteration.
Positive precipitation anomalies are predicted throughout most of the Holocene for both temperature reconstructions (Fig. 6). While differences between the northern and southern flow lines are relatively minor, there are significant differences in precipitation between the Buizert et al. (2018) and Dahl-Jensen et al. (1998) inversions. In the Buizert et al. (2018) inversion, the largest precipitation anomalies (up to 1 m w.e. a−1) occur during the early Holocene. Precipitation remains relatively high during the HTM (10–6 ka) but dips before the 8.2 ka cold event. For the Dahl-Jensen et al. (1998) inversion, ΔP is relatively low during the early Holocene but increases during the HTM (8.5–3 ka). Unlike the Buizert et al. (2018) inversion, there is an evident trend between HTM warming and increased snowfall (Fig. 9).
Forcing the model with mean estimated precipitation anomalies yields plausible retreat histories on both flow lines. Modeled and observed retreat chronologies match within uncertainty (Fig. 8). A significant fraction of Holocene precipitation (typically >90 %) falls as snow. Hence, a positive precipitation anomaly can be interpreted directly as additional snowfall and snow accumulation. Average HTM snowfall is around 35 % higher than modern in both temperature reconstructions (Fig. 9). However, overall trends in Holocene snowfall differ between reconstructions.
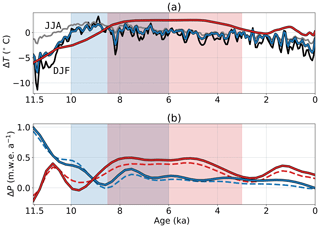
Figure 6(a) Buizert et al. (2018) and Dahl-Jensen et al. (1998) mean annual temperature anomalies are shown as blue and red lines, respectively. Gray and black lines, respectively, show average December, January, February (DJF) and June, July, August (JJA) temperature anomalies for the Buizert et al. (2018) reconstruction. Shaded blue and pink regions demarcate the extent of the HTM for the Buizert et al. (2018) and Dahl-Jensen et al. (1998) reconstructions. (b) Estimated precipitation anomaly histories for the Buizert et al. (2018) and Dahl-Jensen et al. (1998) inversions are shown by blue and red lines, respectively. Solid lines show estimates for the northern flow line, while dashed lines are for the southern flow line.
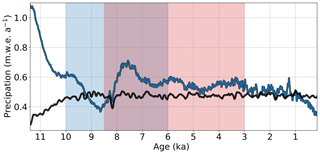
Figure 7Average precipitation (both solid and liquid) on the northern flow line from the Buizert et al. (2018) reconstruction (black line), which is based on the TraCE-21ka coupled ocean–atmosphere general circulation model of the last deglaciation versus estimated precipitation derived in this work based on reconciling the modeled and observed retreat chronologies (blue line).
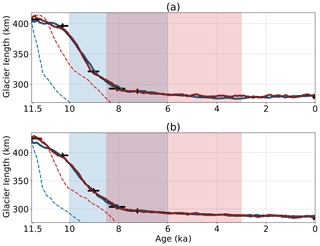
Figure 8Modeled retreat histories for the northern (a) and southern (b) flow lines using a variety of ΔT and ΔP forcings. Blue and red lines show modeled retreat using Buizert et al. (2018) and Dahl-Jensen et al. (1998) temperature forcings, respectively. Dashed lines show the results of forcing the model with ΔP=0, while solid lines show the results of using optimal estimated precipitation anomalies. Black diamonds and bars show reconstructed terminus positions, along with 95 % confidence intervals. Shaded blue and pink regions demarcate the extent of the HTM for the Buizert et al. (2018) and Dahl-Jensen et al. (1998) reconstructions, respectively.
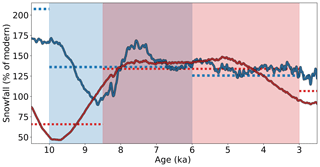
Figure 9HTM snowfall averaged across the northern and southern flow lines for the Buizert et al. (2018) (solid blue line) and Dahl-Jensen et al. (1998) (solid red line) inversions. Shaded blue and pink regions demarcate the extent of the HTM for the Buizert et al. (2018) and Dahl-Jensen et al. (1998) reconstructions, respectively. Dashed lines show pre-HTM, HTM, and post-HTM average snowfall for each inversion.
3.3 Sensitivity testing
We assess the sensitivity of Holocene precipitation anomalies to modeling uncertainties by performing an HTM inversion using the methodology described in Sect. 2.5.7. To obtain accurate uncertainty estimates, we use a fifth-order accurate sigma point set based on Li et al. (2017) (Appendix A), as we find that the second-order Menegaz et al. (2011) set likely underestimates covariance. Inversions are performed on the northern flow line using the Buizert et al. (2018) temperature reconstruction. Model runs are initialized from steady states around at 10.5 ka, 500 years prior to the Buizert et al. (2018) HTM. Prior and posterior parameter values are reported in Table 3.
Table 3Summary of primary model parameters used in this work. Default values are provided where applicable. Prior parameter uncertainties assumed for the sensitivity test are shown in the 2σ column.

Mean HTM precipitation anomalies are within 2 cm w.e. a−1 of the inversion presented in Sect. 3.2 (Fig. 10). Parameter uncertainties contribute to uncertainty in ΔP. Overall, however, temperature uncertainty is far more significant than uncertainty in model parameters. Differences in model initialization do not significantly impact the results of the inversion. Although sensitivity tests are initialized from steady states at 10.5 ka, while inversions in Sect. 3.2 are initialized from a transient state at 11.6 ka, the mean HTM precipitation anomalies are nearly identical. Estimated posterior parameter values are also similar to the assumed prior values (Table 3).
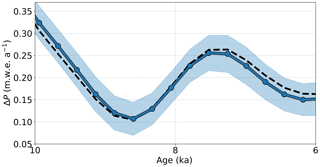
Figure 10The blue line and shaded region show the estimated mean ΔP and 95 % confidence bands, respectively, for the sensitivity test, accounting for uncertainty in a number of ice flow and PDD model parameters. The dashed black line shows the mean estimated ΔP from a previous inversion assuming no uncertainty in model parameters.
We infer changes in Holocene precipitation in the Kangerlussuaq region of western Greenland using a new chronology of ice sheet terminus position from Young et al. (2020) and an inverse modeling procedure based on the unscented transform. We find that scaling precipitation with temperature via the Clausius–Clapeyron equation (Eq. 4) results in excessively fast retreat during the early Holocene for both the Buizert et al. (2018) and Dahl-Jensen et al. (1998) temperature reconstructions. Thus, temperature-driven changes in precipitation and accumulation alone are not sufficient to reproduce the observed pattern of retreat. Inversions show that adding precipitation throughout the Holocene and specifically during the HTM yields a good fit to observations (Figs. 6, 8). Since a large fraction of precipitation falls as snow, a positive precipitation anomaly can be interpreted fairly directly as an increase in accumulation beyond what would be expected from temperature changes alone.
There are considerable differences in predicted precipitation anomalies depending on the assumed temperature history. Inversions using the Buizert et al. (2018) temperature reconstruction show generally decreasing snowfall through the Holocene. Due to high snowfall in the early Holocene (nearly 100 % higher than modern) and a dip in HTM precipitation associated with the 8.2 ka cold event, average HTM snowfall roughly matches the overall Holocene average, which is about 35 % above modern. In contrast, inversions using the Dahl-Jensen et al. (1998) temperature reconstruction show a clear trend between HTM warming and increased snowfall (Fig. 9). This trend could be interpreted as a transient increase in snowfall due to reduced Arctic sea ice cover or changes in atmospheric circulation during the HTM.
A large positive ΔP correction during the early Holocene in the Buizert et al. (2018) inversion likely reflects the dependence of precipitation on temperature. Low temperatures during the early Holocene result in low precipitation. Without an additional moisture source to increase snowfall, the ice sheet retreats far more rapidly than observed. In the Dahl-Jensen et al. (1998) reconstruction, warming occurs more gradually in the early Holocene. Accumulation and ablation are more closely balanced, resulting in a smaller precipitation anomaly correction from 11.6 to 10 ka.
When interpreting results of precipitation inversions, it is important to consider that the Buizert et al. (2018) and Dahl-Jensen et al. (1998) reconstructions are obtained using different methodologies. The Greenland-wide Buizert et al. (2018) reconstruction is obtained by merging the TraCE-21ka coupled ocean–atmosphere general circulation model of the last deglaciation (Liu et al., 2009; He et al., 2013) with borehole temperature reconstructions at GISP2, NGRIP, and NEEM. Our estimated precipitation history in the Kangerlussuaq region is significantly different from TraCE-21ka, particularly during the early Holocene and parts of the HTM (Fig. 7). In contrast to Buizert et al. (2018), the Dahl-Jensen et al. (1998) temperature reconstruction at GRIP offers only a pointwise estimate containing no explicit spatial or seasonal information.
While the Buizert et al. (2018) temperature reconstruction is arguably more suitable for our purposes, since it resolves spatial and seasonal patterns in ΔT, there is still considerable uncertainty in temperature, particularly near the ice margins. Despite this, there is some consensus between the Buizert et al. (2018) and Dahl-Jensen et al. (1998) inversions. For example, average HTM snowfall is roughly 35 % higher than modern in both cases (Fig. 9).
Predicted HTM precipitation anomalies are not particularly sensitive to uncertainties in the ice sheet or PDD model parameters or the initialization procedure. In the sensitivity test presented in Sect. 3.3, model runs are initialized using steady states at 10.5 ka. Runs in the full Holocene inversions in Sect. 3.2, which use fixed parameter sets, are initialized from a transient state at 11.6 ka. Even considering these differences in model initialization, estimated HTM precipitation anomalies are comparable in all inversions (Fig. 10). Additionally, ΔP does not appear to be sensitive to uncertainties in bedrock geometry, as inversions conducted with a static bedrock geometry yielded similar results to inversions accounting for isostatic uplift.
Significant strides have been made in time-dependent data assimilation in glaciology using adjoint-based methods. Goldberg and Heimbach (2013) infer the initial thickness and basal conditions for a synthetic ice sheet given snapshots of ice thickness at discrete times. Larour et al. (2014) demonstrate a data assimilation framework within the Ice Sheet System Model (ISSM), capable of obtaining temporal estimates of surface mass balance and basal friction given surface altimetry.
In contrast to adjoint-based approaches, the unscented transform (UT) does not require computing the Jacobian or Hessian of an objective function or a special checkpointing code for time-dependent problems. Adjoint-based methods are advantageous for extremely high-dimensional problems, as the required number of model runs is independent of the number of parameters. However, the UT provides more accurate uncertainty estimates than linearization (Julier and Uhlmann, 1997). Hessian information can be used to improve uncertainty estimates (Isaac et al., 2015). However, this methodology uses purely local approximations to the nonlinear function around the maximum a posteriori probability (MAP) estimator, which may affect the quality of uncertainty estimates.
The unscented transform has advantages over Markov chain Monte Carlo methods for inference problems with a relatively small number of unknown parameters (<1000 or so parameters). In this work, we optimize for n=44 parameters representing precipitation anomaly values at discrete points in time. Since function evaluations at each sigma point are independent, the UT is trivially parallelizable. Consequently, on a high-end desktop, the iterative optimization process presented in Sect. 2.5.6 takes roughly the same amount of time as performing three successive forward model runs.
MCMC methods can be parallelized to some extent by utilizing multiple interacting Markov chains running in parallel (e.g., Chowdhury and Jermaine, 2018) or by combining samples from independent chains in a post-processing step (e.g., Neiswanger et al., 2013). Nonetheless, computational bottlenecks persist in MCMC methods since individual Markov chains are inherently serial. Consequently, UT approximations to the posterior distribution can be generated hundreds to thousands of times faster for small parameter sets.
A drawback of the UT is that its accuracy is inherently limited by using a predetermined number of sample points. In our case, for example, using a minimal set of n+1 sigma points for n unknown parameters yields accurate mean estimates but appears to underestimate covariance when compared to a higher-order cubature method. Without testing multiple sigma point sets and scaling parameters, it can be difficult to assess the accuracy of UT estimates of the posterior. MCMC methods, in contrast, can provide arbitrarily accurate estimates of the posterior given sufficient computation time. Moreover, they can resolve the full posterior distribution rather than computing its moments as in the UT.
An alternative to traditional MCMC methods is to use surrogate models or emulators (Gong and Duan, 2017). Here, a computationally inexpensive surrogate model is trained to approximate the output of a more complex model function. The surrogate model can then be used in place of the full model for the purpose of MCMC sampling, significantly reducing the overall computational cost. A few types of surrogate models have already been applied to glaciological problems including deep neural networks (Tarasov et al., 2012) and Gaussian processes (e.g., Chang et al., 2016; Pollard et al., 2016).
Surrogate models require an initial training phase. Pollard et al. (2016), for example, perform 625 ice sheet model runs using combinations of four unknown simulation parameters. A Gaussian process surrogate model is then fitted to this training data in order to interpolate the model in parameter space for inference. The number and selection of training points significantly affects the performance of the surrogate model.
Interestingly, there is a strong connection between the unscented transform and Gaussian process surrogate models. It can be shown that sigma points for the UT are optimal training points for a Gaussian process surrogate model in the sense of minimizing the variance of the expected value of the posterior distribution (Särkkä et al., 2016). While the details are technical, one can think of UT sigma points as optimal training points given that (i) the prior distribution is a multivariate Gaussian and (ii) the Gaussian process surrogate model has a polynomial covariance function.
5.1 Modeling conclusions
Our work follows a number of previous observationally constrained paleo-ice sheet modeling studies (e.g., Tarasov and Peltier, 2002; Lecavalier et al., 2014; Calov et al., 2015). Perhaps most relevant to this work is Lecavalier et al. (2014), who model the deglaciation of Greenland from the Last Glacial Maximum (LGM) using a 3D thermomechanically coupled ice sheet model. Model runs in Lecavalier et al. (2014) are informed by constraints on relative sea level, ice core thinning, and LGM ice sheet extent.
In contrast to previous modeling studies, the computational efficiency of the flow line model outlined in Brinkerhoff et al. (2017) makes time-dependent data-assimilation, sensitivity testing, and robust uncertainty estimation tractable. Sensitivity testing indicates that estimated precipitation is insensitive to parameter uncertainties in the PDD and ice dynamics models. This conclusion supports earlier findings showing that modeled Holocene retreat in land-terminating sectors of the GrIS is more sensitive to surface mass balance than other factors like the flow law or basal sliding (Cuzzone et al., 2019; Lecavalier et al., 2014).
A drawback of our modeling approach is that we cannot account for inherent map plane effects such as changes in ice flow direction, or convergent or divergent flow in or out of the assumed flow path. These factors likely contribute to small discrepancies in estimated precipitation anomalies between the northern and southern flow lines (Fig. 6). Beyond computational efficiency, there are number of reasons why a flow line model is appropriate for our purposes. The modern flow field near Kangerlussuaq can be characterized by relatively simple east-to-west flow, and there is an absence of strongly convergent flow into outlet glaciers. Given the low bedrock relief in the region, and the surface-mass-balance-dominated retreat pattern (Van Tatenhove et al., 1996; Cuzzone et al., 2019), it is reasonable to assume that the flow regime was similar during the Holocene. In this work, we do not treat temperature as a random variable with its own covariance structure. However, differences between the Buizert et al. (2018) and Dahl-Jensen et al. (1998) inversions indicate that temperature is the dominant source of uncertainty in ΔP. This result underscores the importance of generating improved, regionally specific, temperature reconstructions constrained by proxy records. More regionally specific estimates of temperature would help to decrease uncertainty in the estimated precipitation history.
Despite lingering uncertainties, our modeling results indicate that the Holocene thermal maximum was accompanied by elevated snowfall, which slowed ice retreat in the Kangerlussuaq region of the GrIS. Inversions conducted using both the Buizert et al. (2018) and Dahl-Jensen et al. (1998) temperature reconstructions show average HTM snowfall around 35 % higher than modern. More specifically, in the Dahl-Jensen et al. (1998) inversion, there is a clear trend between HTM warming and increased accumulation, which could be interpreted as transient increase in precipitation due to reduced Arctic sea ice cover or changes in atmospheric circulation.
Estimating the mean and covariance of the posterior distribution requires approximating Gaussian-weighted expectation integrals of the form
via numerical integration rules, also called cubature rules, which approximate the expectation integral as a weighted sum
Here, the notation ) refers to a Gaussian probability density function evaluated at the point x. General Gaussian weight functions ) are handled by changing variables. Letting be a matrix square root of the covariance matrix, we have
Cubature rules, including the unscented transform, are constructed to exactly integrate polynomial functions ℱ(x) up to a certain degree d. Suppose that is a point in ℝn. A monomial of degree d refers to a function , where the exponents are nonnegative integers that sum to d. A polynomial of degree d is a linear combination of monomials with highest degree d.
Li et al. (2017) describe a fifth-order cubature rule using fully symmetric sets of sigma points. A set is fully symmetric if it is closed under the operations of coordinate position and sign permutations. Their cubature rule has the form
The notation ) refers to a sum of the function ℱ evaluated at all points in the fully symmetric set generated by the given point.
Due to the symmetry of the sigma points and the Gaussian weight function, all moments (that is, integrals of Gaussian-weighted monomial functions) containing an odd order exponent are automatically satisfied. Exploiting this fact and the symmetries of the sigma points, it can be shown that satisfying the remaining moment constraint equations up the fifth order reduces to solving the following system of four equations in four unknowns and λ
By slightly modifying this cubature rule
we introduce a new free parameter λ2 that allows scaling of the sigma points about the mean. The new moment constraint equations become
Using E[1]=1, , , and we obtain
with n>4 and . A drawback of the original cubature rule, as well our modified version here, is that it requires negative weights, which can lead to numerical instability.
The flow line ice sheet model and PDD model used in this work are available at https://github.com/JacobDowns/flow_model (last access: March 2020, Downs, 2020).
JD was the lead author of this paper. JJ and JC assisted JD with ice sheet modeling efforts. JB, NY, and AL provided the moraine age data used in this work. JD and JJ wrote the manuscript with input from all authors.
The authors declare that they have no conflict of interest.
Jacob Downs and Jesse Johnson were supported by NSF grant 1504457. Jacob Downs would like to thank Doug Brinkerhoff for providing code for the flow line ice sheet model used in this work, as well as many elucidating discussions. Jacob Downs would also like to thank John Bardsley for providing many mathematical insights into inverse problems. Our thanks to the reviewers and editor who helped to significantly improve the quality of this paper.
This research has been supported by the National Science Foundation (grant no. 1504457).
This paper was edited by Kerim Nisancioglu and reviewed by Lev Tarasov and Stephen Price.
Abe-Ouchi, A., Segawa, T., and Saito, F.: Climatic Conditions for modelling the Northern Hemisphere ice sheets throughout the ice age cycle, Clim. Past, 3, 423–438, https://doi.org/10.5194/cp-3-423-2007, 2007. a, b
Alley, R. B., Meese, D. A., Shuman, C. A., Gow, A. J., Taylor, K. C., Grootes, P. M., White, J. W., Ram, M., Waddington, E. D., Mayewski, P. A., and Zielinski, G. A.: Abrupt increase in Greenland snow accumulation at the end of the Younger Dryas event, Nature, 362, 527–529, https://doi.org/10.1038/362527a0, 1993. a
Bahadory, T. and Tarasov, L.: LCice 1.0 – a generalized Ice Sheet System Model coupler for LOVECLIM version 1.3: description, sensitivities, and validation with the Glacial Systems Model (GSM version D2017.aug17), Geosci. Model Dev., 11, 3883–3902, https://doi.org/10.5194/gmd-11-3883-2018, 2018. a
Bintanja, R. and Selten, F. M.: Future increases in Arctic precipitation linked to local evaporation and sea-ice retreat, Nature, 509, 479–482, https://doi.org/10.1038/nature13259, 2014. a, b
Blatter, H.: Velocity and stress fields in grounded glaciers: a simple algorithm for including deviatoric stress gradients, J. Glaciol., 41, 333–344, https://doi.org/10.1017/S002214300001621X, 1995. a
Box, J. E.: Greenland ice sheet mass balance reconstruction. Part II: Surface mass balance (1840–2010), J. Climate, 26, 6974–6989, https://doi.org/10.1175/JCLI-D-12-00518.1, 2013. a, b
Brinkerhoff, D., Truffer, M., and Aschwanden, A.: Sediment transport drives tidewater glacier periodicity, Nat. Commun., 8, 90, https://doi.org/10.1038/s41467-017-00095-5, 2017. a, b, c
Buizert, C., Keisling, B. A., Box, J. E., He, F., Carlson, A. E., Sinclair, G., and DeConto, R. M.: Greenland-Wide Seasonal Temperatures During the Last Deglaciation, Geophys. Res. Lett., 45, 1905–1914, https://doi.org/10.1002/2017GL075601, 2018. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, aa, ab, ac, ad, ae, af, ag
Calov, R., Robinson, A., Perrette, M., and Ganopolski, A.: Simulating the Greenland ice sheet under present-day and palaeo constraints including a new discharge parameterization, The Cryosphere, 9, 179–196, https://doi.org/10.5194/tc-9-179-2015, 2015. a
Caron, L., Ivins, E. R., Larour, E., Adhikari, S., Nilsson, J., and Blewitt, G.: GIA Model Statistics for GRACE Hydrology, Cryosphere, and Ocean Science, Geophys. Res. Lett., 45, 2203–2212, https://doi.org/10.1002/2017GL076644, 2018. a, b
Chang, W., Haran, M., Applegate, P., and Pollard, D.: Calibrating an Ice Sheet Model Using High-Dimensional Binary Spatial Data, J. Am. Stat. Assoc., 111, 57–72, https://doi.org/10.1080/01621459.2015.1108199, 2016. a
Chib, S. and Greenberg, E.: Understanding the metropolis-hastings algorithm, Am. Stat., 49, 327–335, https://doi.org/10.1080/00031305.1995.10476177, 1995. a, b
Chowdhury, A. and Jermaine, C.: Parallel and Distributed MCMC via Shepherding Distributions, Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics, 84, 1819–1827, 2018. a
Cuzzone, J. K., Schlegel, N.-J., Morlighem, M., Larour, E., Briner, J. P., Seroussi, H., and Caron, L.: The impact of model resolution on the simulated Holocene retreat of the southwestern Greenland ice sheet using the Ice Sheet System Model (ISSM), The Cryosphere, 13, 879–893, https://doi.org/10.5194/tc-13-879-2019, 2019. a, b, c, d, e, f
Dahl-Jensen, D., Mosegaard, K., Gundestrup, N., Clow, G. D., Johnsen, S. J., Hansen, A. W., and Balling, N.: Past temperatures directly from the Greenland Ice Sheet, Science, 282, 268–271, https://doi.org/10.1126/science.282.5387.268, 1998. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, aa, ab, ac
Downs, J.: flow_model (Version v1.0), figshare, available at: https://github.com/JacobDowns/flow_model, http://doi.org/10.6084/m9.figshare.11923896, last access: March 2020. a
Goldberg, D. N. and Heimbach, P.: Parameter and state estimation with a time-dependent adjoint marine ice sheet model, The Cryosphere, 7, 1659–1678, https://doi.org/10.5194/tc-7-1659-2013, 2013. a
Gong, W. and Duan, Q.: An adaptive surrogate modeling-based sampling strategy for parameter optimization and distribution estimation (ASMO-PODE), Environ. Modell. Softw., 95, 61–75, https://doi.org/10.1016/j.envsoft.2017.05.005, 2017. a
He, F., Shakun, J. D., Clark, P. U., Carlson, A. E., Liu, Z., Otto-Bliesner, B. L., and Kutzbach, J. E.: Northern Hemisphere forcing of Southern Hemisphere climate during the last deglaciation, Nature, 494, 81–85, https://doi.org/10.1038/nature11822, 2013. a
Isaac, T., Petra, N., Stadler, G., and Ghattas, O.: Scalable and efficient algorithms for the propagation of uncertainty from data through inference to prediction for large-scale problems, with application to flow of the Antarctic ice sheet, J. Comput. Phys., 296, 348–368, https://doi.org/10.1016/j.jcp.2015.04.047, 2015. a
Johannesson, T., Sigurdsson, O., Laumann, T., and Kennett, M.: Degree-day glacier mass-balance modelling with applications to glaciers in Iceland, Norway and Greenland, J. Glaciol., 41, 345–358 https://doi.org/10.1017/S0022143000016221, 1995. a, b
Julier, S. J. and Uhlmann, J. K.: New extension of the Kalman filter to nonlinear systems, Int Symp AerospaceDefense Sensing Simul and Controls, https://doi.org/10.1117/12.280797, 1997. a, b, c, d, e
Kaufman, D. S., Ager, T. A., Anderson, N. J., Anderson, P. M., Andrews, J. T., Bartlein, P. J., Brubaker, L. B., Coats, L. L., Cwynar, L. C., Duvall, M. L., Dyke, A. S., Edwards, M. E., Eisner, W. R., Gajewski, K., Geirsdóttir, A., Hu, F. S., Jennings, A. E., Kaplan, M. R., Kerwin, M. W., Lozhkin, A. V., MacDonald, G. M., Miller, G. H., Mock, C. J., Oswald, W. W., Otto-Bliesner, B. L., Porinchu, D. F., Rühland, K., Smol, J. P., Steig, E. J., and Wolfe, B. B.: Holocene thermal maximum in the western Arctic (0–180∘ W), Quat. Sci. Rev., 23, 2059–2060, https://doi.org/10.1016/j.quascirev.2003.09.007, 2004. a, b
Kobashi, T., Menviel, L., Jeltsch-Thömmes, A., Vinther, B. M., Box, J. E., Muscheler, R., Nakaegawa, T., Pfister, P. L., Döring, M., Leuenberger, M., Wanner, H., and Ohmura, A.: Volcanic influence on centennial to millennial Holocene Greenland temperature change, Sci. Rep., 7, 1441, https://doi.org/10.1038/s41598-017-01451-7, 2017. a
Larour, E., Utke, J., Csatho, B., Schenk, A., Seroussi, H., Morlighem, M., Rignot, E., Schlegel, N., and Khazendar, A.: Inferred basal friction and surface mass balance of the Northeast Greenland Ice Stream using data assimilation of ICESat (Ice Cloud and land Elevation Satellite) surface altimetry and ISSM (Ice Sheet System Model), The Cryosphere, 8, 2335–2351, https://doi.org/10.5194/tc-8-2335-2014, 2014. a
Lecavalier, B. S., Milne, G. A., Simpson, M. J., Wake, L., Huybrechts, P., Tarasov, L., Kjeldsen, K. K., Funder, S., Long, A. J., Woodroffe, S., Dyke, A. S., and Larsen, N. K.: A model of Greenland ice sheet deglaciation constrained by observations of relative sea level and ice extent, Quat. Sci. Rev., 102, 54–84, https://doi.org/10.1016/j.quascirev.2014.07.018, 2014. a, b, c, d, e, f
Li, Z., Yang, W., Ding, D., and Liao, Y.: A Novel Fifth-Degree Cubature Kalman Filter for Real-Time Orbit Determination by Radar, Math. Probl. Eng., 2017, 8526804, https://doi.org/10.1155/2017/8526804, 2017. a, b
Liu, Z., Otto-Bliesner, B. L., He, F., Brady, E. C., Tomas, R., Clark, P. U., Carlson, A. E., Lynch-Stieglitz, J., Curry, W., Brook, E., Erickson, D., Jacob, R., Kutzbach, J., and Cheng, J.: Transient simulation of last deglaciation with a new mechanism for bolling-allerod warming, Science, 325, 310–314, https://doi.org/10.1126/science.1171041, 2009. a
Marcott, S. A., Shakun, J. D., Clark, P. U., and Mix, A. C.: A reconstruction of regional and global temperature for the past 11 300 years, Science, 339, 1198–1201, https://doi.org/10.1126/science.1228026, 2013. a
Menegaz, H. M., Ishihara, J. Y., and Borges, G. A.: A new smallest sigma set for the Unscented Transform and its applications on SLAM, in: Proceedings of the IEEE Conference on Decision and Control, 2011, 3172–3177, https://doi.org/10.1109/CDC.2011.6161480, 2011. a, b, c, d, e
Miller, G. H., Brigham-Grette, J., Alley, R. B., Anderson, L., Bauch, H. A., Douglas, M. S., Edwards, M. E., Elias, S. A., Finney, B. P., Fitzpatrick, J. J., Funder, S. V., Herbert, T. D., Hinzman, L. D., Kaufman, D. S., MacDonald, G. M., Polyak, L., Robock, A., Serreze, M. C., Smol, J. P., Spielhagen, R., White, J. W., Wolfe, A. P., and Wolff, E. W.: Temperature and precipitation history of the Arctic, Quat. Sci. Rev., 19, 2841–2843 https://doi.org/10.1016/j.quascirev.2010.03.001, 2010. a
Morlighem, M., Williams, C. N., Rignot, E., An, L., Arndt, J. E., Bamber, J. L., Catania, G., Chauché, N., Dowdeswell, J. A., Dorschel, B., Fenty, I., Hogan, K., Howat, I., Hubbard, A., Jakobsson, M., Jordan, T. M., Kjeldsen, K. K., Millan, R., Mayer, L., Mouginot, J., Noël, B. P., O'Cofaigh, C., Palmer, S., Rysgaard, S., Seroussi, H., Siegert, M. J., Slabon, P., Straneo, F., van den Broeke, M. R., Weinrebe, W., Wood, M., and Zinglersen, K. B.: BedMachine v3: Complete Bed Topography and Ocean Bathymetry Mapping of Greenland From Multibeam Echo Sounding Combined With Mass Conservation, Geophys. Res. Lett., 44, 11051–11061, https://doi.org/10.1002/2017GL074954, 2017. a, b
Mouginot, J., Rignot, E., Scheuchl, B., and Millan, R.: Comprehensive annual ice sheet velocity mapping using Landsat-8, Sentinel-1, and RADARSAT-2 data, Remote Sens., 9, 364, https://doi.org/10.3390/rs9040364, 2017. a, b
Neiswanger, W., Wang, C., and Xing, E.: Asymptotically Exact, Embarrassingly Parallel MCMC, Proceeding UAI'14 Proceedings of the Thirtieth Conference on Uncertainty in Artificial Intelligence, available at: http://arxiv.org/abs/1311.4780, 1–16, 2013. a
Pattyn, F.: A new three-dimensional higher-order thermomechanical ice sheet model: Basic sensitivity, ice stream development, and ice flow across subglacial lakes, J. Geophys. Res., 108, 2382, https://doi.org/10.1029/2002JB002329, 2003. a
Pollard, D., Chang, W., Haran, M., Applegate, P., and DeConto, R.: Large ensemble modeling of the last deglacial retreat of the West Antarctic Ice Sheet: comparison of simple and advanced statistical techniques, Geosci. Model Dev., 9, 1697–1723, https://doi.org/10.5194/gmd-9-1697-2016, 2016. a, b
Polyak, L., Alley, R. B., Andrews, J. T., Brigham-Grette, J., Cronin, T. M., Darby, D. A., Dyke, A. S., Fitzpatrick, J. J., Funder, S., Holland, M., Jennings, A. E., Miller, G. H., O'Regan, M., Savelle, J., Serreze, M., St. John, K., White, J. W., and Wolff, E.: History of sea ice in the Arctic, Quat. Sci. Rev., 29, 1757–1778, https://doi.org/10.1016/j.quascirev.2010.02.010, 2010. a
Rasmussen, C. E.: Gaussian Processes in Machine Learning, MIT Press, https://doi.org/10.1.1.86.3414, 2006. a
Reeh, N.: Parameterization of Melt Rate and Surface Temperature on the Greenland lce Sheet, Polarforschung, 21–47, https://doi.org/10.1007/978-3-7091-0973-1_2, 1991. a
Ritz, C., Rommelaere, V., and Dumas, C.: Modeling the evolution of Antarctic ice sheet over the last 420 000 years: Implications for altitude changes in the Vostok region, J. Geophys. Res.-Atmos., 106, 31943–31964, https://doi.org/10.1029/2001JD900232, 2001. a, b
Särkkä, S.: Bayesian Filtering and Smoothing, Cambridge University Press, 1–232, https://doi.org/10.1017/CBO9781139344203, 2013. a, b
Särkkä, S., Hartikainen, J., Svensson, L., and Sandblom, F.: On the relation between Gaussian process quadratures and sigma-point methods, in: Journal of Advances in Information Fusion, 11, 31–46, 2016. a
Singarayer, J. S., Bamber, J. L., and Valdes, P. J.: Twenty-first-century climate impacts from a declining Arctic sea ice cover, J. Climate, 19, 1109–1125, https://doi.org/10.1175/JCLI3649.1, 2006. a
Tarasov, L. and Peltier, W. R.: Greenland glacial history and local geodynamic consequences, Geophys. J. Int., 150, 198–229, https://doi.org/10.1046/j.1365-246X.2002.01702.x, 2002. a
Tarasov, L., Dyke, A. S., Neal, R. M., and Peltier, W. R.: A data-calibrated distribution of deglacial chronologies for the North American ice complex from glaciological modeling, Earth Planet. Sc. Lett., 315, 30–40, https://doi.org/10.1016/j.epsl.2011.09.010, 2012. a
Thomas, E. K., Briner, J. P., Ryan-Henry, J. J., and Huang, Y.: A major increase in winter snowfall during the middle Holocene on western Greenland caused by reduced sea ice in Baffin Bay and the Labrador Sea, Geophys. Res. Lett., 43, 5302–5308, https://doi.org/10.1002/2016GL068513, 2016. a, b
Van Tatenhove, F. G., Van Der Meer, J. J., and Koster, E. A.: Implications for deglaciation chronology from new AMS age determinations in central West Greenland, Quat. Res., 45, 245–253, https://doi.org/10.1006/qres.1996.0025, 1996. a
Wright, P. J., Harper, J. T., Humphrey, N. F., and Meierbachtol, T. W.: Measured basal water pressure variability of the western Greenland Ice Sheet: Implications for hydraulic potential, J. Geophys. Res.-Ea, 121, 1134–1147, https://doi.org/10.1002/2016JF003819, 2016. a
Young, N. E., Briner, J. P., Miller, G. H., Lesnek, A. J., Crump, S. E., Thomas, E. K., Pendleton, S. L., Cuzzone, J., Lamp, J., Zimmerman, S., Caffee, M., and Schaefer, J. M.: Deglaciation of the Greenland and Laurentide ice sheets interrupted by glacier advance during abrupt coolings, Quat. Sci. Rev., 229, 106091, https://doi.org/10.1016/j.quascirev.2019.106091, 2020. a, b, c, d, e, f, g
According to Jeffrey Uhlmann, the creator of the UT, the term “unscented” was inspired by a stick of deodorant and has no technical significance (Julier and Uhlmann, 1997).
- Abstract
- Introduction
- Numerical methods for inference
- Results
- Discussion
- The unscented transform as a data assimilation method
- Appendix A: A higher-order method for estimating covariance
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Numerical methods for inference
- Results
- Discussion
- The unscented transform as a data assimilation method
- Appendix A: A higher-order method for estimating covariance
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References